论文阅读笔记 | 分类网络——Swin Transformer
如有错误,恳请指出。
文章目录
- 1. Introduction
- 2. Related Work
- 3. Swin Transformer Method
-
- 3.1 Overall Architecture
-
- 3.1.1 Architecture
- 3.1.2 Swin Transformer block
- 3.2 Shifted Window based Self-Attention
-
- 3.2.1 Self-attention in non-overlapped windows
- 3.2.2 Shifted window partitioning in successive blocks
- 3.2.3 Efficient batch computation for shifted configuration
- 4. Result
paper:Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
code:https://github.com/microsoft/Swin-Transformer

摘要:
作者提出了一个新的vision Transformer,称为Swin Transformer,它可以作为计算机视觉的通用backbone(骨干网络)。在此之前,原生Self-Attention的计算复杂度问题一直没有得到解决,Self-Attention需要对输入的所有N个token计算 N 2 N^{2} N2大小的相互关系矩阵。而视觉信息的分辨率通常比较大,所以计算复杂度很难降低。Swin Transformer使用了分层设计(hierarchical design)和移位窗口(shifted window)方法成功解决这个问题。
Swin Transformer在各种计算机视觉任务中有一个较好的效果:
- image classification:87.3 top-1 accuracy on ImageNet-1K
- object detection5:8.7 box AP and 51.1 mask AP on COCO testdev
- semantic segmentation:53.5 mIoU on ADE20K val
原文论述:Its performance surpasses the previous state-of-theart by a large margin of +2.7 box AP and +2.6 mask AP on COCO, and +3.2 mIoU on ADE20K
这展示了基于transformer的模型作为backbone的潜力,同时分层设计和移位窗口方法也证明对全mlp架构是有益的。
1. Introduction
卷积神经网络通过更大的尺度、更广泛的连接、更复杂的卷积形式不断增强着网络性能。cnn作为各种视觉任务的骨干网络,这些架构上的进步导致了性能的提高,广泛提升了整个领域。
Transformer是为序列建模和转换任务而设计的,值得注意的是它将注意力用于建模数据中的长期依赖关系,作者希望其可以作为视觉上的一个通用骨干。但是,其在NLP领域与CV领域的表现具有差异:
1)规模的差异
与在language Transformers中作为基本处理元素的word tokens不同,视觉元素在规模上可以有很大的变化,这是一个在目标检测等任务中受到关注的问题。在现有的基于transformer的模型中,tokens都是固定比例的,这一属性不适合这些视觉应用。
2)分辨率的差异
与文本段落中的文字相比,图像中的像素分辨率要高得多。语义分割等许多视觉任务都需要在像素级进行密集的预测,这对于Transformer在高分辨率图像上是非常棘手的,因为它的自注意计算复杂度是图像大小平方倍。
为此,作者提出了Swin Transformer,其构造层次特征图,并对图像大小具有线性计算复杂度。

如图结构(a)所示,Swin Transformer从较小的patch(用灰色标出)开始,逐步合并更深的Transformer层中相邻的patch,从而构建了一个层次表示。有了这些分层特征映射,Swin Transformer模型可以方便地利用高级技术进行密集预测,如特征金字塔网络(FPN)或U-Net。
线性计算复杂度是通过在非重叠窗口内计算局部自注意来实现的,该窗口对图像进行分割(用红色标出)。每个窗口中的patch数量是固定的,因此复杂度与图像大小成线性关系,复杂度为 O ( N ∗ n ) O(N*n) O(N∗n)。这些优点使Swin Transformer适合作为各种视觉任务的通用骨干,而之前基于Transformer的架构只生成单一分辨率的特征图,具有 O ( N 2 ) O(N^{2}) O(N2)复杂度。

Swin Transformer的一个关键设计元素是它在连续自注意层之间的窗口分区的移位,如上图所示。移位的窗口连接了前一层的窗口,提供了它们之间的连接,显著增强了模型的表达能力。这个策略对于现实世界的延迟也是有效的:窗口中的全部的query patch共享相同的keyset,这有助于硬件中的内存访问。移位窗口方法比滑动窗口方法有更低的延迟,对全mlp架构也有益。
2. Related Work
尽管Vit模型在之前取得了可以媲美SOTA的CNN的表现,但是其仍然存在许多的缺点:
1)需要大规模的训练数据集
2)内存访问昂贵,延迟大
3)参数量大,计算复杂度高
对于第一个问题,DeiT提出了一种新的蒸馏方式,使得不需要额外的训练数据集就可以获取一个比较好的结果,而Swin Transformer提出的移动窗口与分层设计可以解决计算复杂度的问题与内存访问昂贵问题。
其中,复杂度由 O ( N 2 ) O(N^{2}) O(N2)降低为 O ( N ∗ n ) O(N*n) O(N∗n)
3. Swin Transformer Method
3.1 Overall Architecture
3.1.1 Architecture
下图展示了Swin Transformer体系结构的概述(Swin-T版本):

假设输入的RGB图像的分辨率为HxWx3,在Swin Transformer中,与Vit类似,通过一个Patch Partition模型将图像分割为一系列的patch(这一步其实可以通过卷积操作实现,只需要将卷积核kernel_size与步长stride设置为一样即可),这些patch可以看成是一个token,其蕴含着图像的局部信息。
这里假设输入的RGB图像的分辨率为224x224x3,假如设置patch size为4,那么一个patch的维度就为4x4x3,将其设置为一个向量值即4x4x3=48,将一个矩阵形式变换为一个向量的形式,通过一个向量来表示一个patch的信息。而如果patch size为4,那么原RGB图像会切分成: p a t c h n u m s = H 4 × W 4 = 56 × 56 patchnums = \frac{H}{4} \times \frac{W}{4} = 56 \times 56 patchnums=4H×4W=56×56个patch,所以目前所得出输出维度是56x56x48(56x56表示patch的数量,48表示一个patch的线性维度信息),再将48这个原始的特征值通过一个Linear Embedding,将其投影到C大小的维度上,也就是由56x56x48转换为56x56xC。接着这些patch tokens会输入到几个带有修改过的自注意计算的Transformer块(Swin Transformer block)中。在Swin Transformer block中会保持tokens的数量,也就是保持56x56的数值不变。Swin Transformer block与Linear Embedding的共同作用称为阶段一“Stage 1”。
而为了实现CNN的类似效果,产生层次化的表示,随着网络的深入,token的数量应该不断的减小,在Swin Transformer中通过Patch Merging来实现token减少的功能。Patch Merging会将每个组2x2的邻近patch的特征连接起来,然后对连接起来的特征再应用到一个线性层上。对于stage 2的特征输出维度是C,所以2x2的邻近patch的特征连接起来的特征维度是4C,这里设置输出维度为2C。在这个过程中,token减少了4倍的数量,行宽都做了一个2倍的下采样。对token数量进行降维之后,然后采用Swin Transformer block进行特征变换,这里同样会保持tokens的数量: p a t c h n u m s = H 8 × W 8 = 28 × 28 patchnums = \frac{H}{8} \times \frac{W}{8} = 28\times 28 patchnums=8H×8W=28×28.这第一块的Patch Merging与Swin Transformer block称为阶段二“Stage 2”。对这个过程再重复两遍,分别为“Stage 3”和“Stage 4”,输出的分辨率分别是: H 16 × W 16 = 14 × 14 \frac{H}{16} \times \frac{W}{16} = 14\times 14 16H×16W=14×14、 H 32 × W 32 = 7 × 7 \frac{H}{32} \times \frac{W}{32} = 7\times 7 32H×32W=7×7。可以看见,每通过一个阶段token的数量都减少4倍。
以上的流程,以224x224x3的图像输入为例,其token数量变化与输出的维度的变化过程如下所示:
- Patch Partition:224x224x3 >> 56x56x48
- Stage 1:patchnums = (224/4)x(224/4)=56x56, shape:56x56x48 >> 56x56xC (48->C)
- Stage 2:patchnums = (224/8)x(224/8)=28x28, shape:56x56xC >> 28x28x2C(C->4C->2C)
- Stage 3:patchnums = (224/16)x(224/16)=14x14, shape:28x28x2C >> 14x14x4C(2C->8C->4C)
- Stage 3:patchnums = (224/32)x(224/32)=7x7, shape:14x14x4C >> 7x7x8C(4C->16C->8C)
可以看见token整个维度变化的流程,token的数量长宽不断的减少一半,但是其线性的维度会增加一倍。这个流程其实和图像的卷积宽高减半,channels加倍是类似的效果,而且网络最后得到的维度为7x7x8C,这其实是类似了很多的CNN最后得到的特征矩阵。在Swin Transformer中,最后的输出可以看成是7x7=49个合并的tokens,每个token蕴含着8C维度的信息。同时对于卷积神经网络来说,这也可以看成是一个7x7大小的特征矩阵,而其channels为8C。
至此,Swin Transformer已经达到了与CNN类似的层次化金字塔结构的降维效果,与典型卷积网络相同的特征图分辨率。因此,该体系结构可以方便地替代现有的各种视觉任务方法中的骨干网络。
3.1.2 Swin Transformer block
Swin Transformer是通过将Transformer块中的标准多头自注意(MSA)模块替换为基于移位窗口(shifted windows)的模块而构建的,其他层保持不变。
Swin Transformer块由一个基于移位窗口(shifted windows)的MSA模块组成,随后是一个激活函数为GELU非线性的2层MLP。每个MSA模块和每个MLP前加LayerNorm (LN)层,每个模块后加残余连接。
W-MSA和SW-MSA分别是具有规则窗型(regular windowing)和移位窗型(shifted windowing)的多头自注意模块。特别注意,Swin Transformer block是不改变token的数量的,改变token数量的是Patch Merging模块。
3.2 Shifted Window based Self-Attention
标准的Transformer架构及其对图像分类的适应性都进行全局自注意,也就是计算一个token与所有其他token之间的关系。全局计算导致了token数量平方的复杂性,计算复杂度为 O ( N 2 ) O(N^{2}) O(N2),使得它不适用于许多需要大量token集进行密集预测或表示高分辨率图像的视觉问题。
3.2.1 Self-attention in non-overlapped windows
之前也说了,如果对全局做注意力处理,计算复杂度比较庞大,所以为了高效的建立模型,作者建议对局部的窗口内做自注意力处理,而不是对整个图像。
窗口以非重叠的方式均匀地划分图像,假设每个窗口包含MxM个patch,而整个图像包含hxw个patch,那么全局多头注意力机制(global MSA module,MSA)与基于窗口的多头注意力机制(window based MSA module,W-MSA)的计算复杂度分别为:
Ω ( M S A ) = 4 h w C 2 + 2 ( h w ) 2 C Ω ( W _ M S A ) = 4 h w C 2 + 2 M 2 h w C \begin{aligned} Ω(MSA) &= 4hwC^{2} + 2(hw)^{2}C \\ Ω(W\_MSA) &= 4hwC^{2} + 2M^{2}hwC \end{aligned} Ω(MSA)Ω(W_MSA)=4hwC2+2(hw)2C=4hwC2+2M2hwC
对于全局多头注意力机制(MSA)其计算复杂度与hw的平方相关,而后者的基于窗口的多头注意力机制(W-MSA),当M固定时,其计算复杂度是线性的(默认设置为7)。全局自注意计算对于大型hw来说通常是负担不起的,而基于窗口的自注意是可伸缩的。
对于上述公式的推理补充:

参考来源:https://zhuanlan.zhihu.com/p/360513527
3.2.2 Shifted window partitioning in successive blocks
W-MSA虽然降低了计算复杂度,但是不重合的window之间缺乏信息交流。于是作者进一步引入shifted window partition来解决不同window的信息交流问题,在两个连续的Swin Transformer Block中交替使用W-MSA和SW-MSA。

上图2为例,将前一层Swin Transformer Block的8x8尺寸feature map划分成2x2个patch,每个patch尺寸为4x4(也就是M=4),然后将下一层Swin Transformer Block的window位置进行移动,得到3x3个不重合的patch。移动window的划分方式使上一层相邻的不重合window之间引入连接,大大的增加了感受野。
W-MSA和SW-MSA的数学表达式为:
z ^ l = W _ M S A ( L N ( z l − 1 ) ) + z l − 1 z l = M L P ( L N ( z ^ l ) ) + z ^ l z ^ l + 1 = S W _ M S A ( L N ( z l ) ) + z l z l + 1 = M L P ( L N ( z ^ l + 1 ) ) + z ^ l + 1 \begin{aligned} \hat{z}^{l} &= W\_MSA(LN(z^{l-1})) + z^{l-1} \\ z^{l} &= MLP(LN(\hat{z}^{l})) + \hat{z}^{l} \\ \hat{z}^{l+1} &= SW\_MSA(LN(z^{l})) + z^{l} \\ z^{l+1} &= MLP(LN(\hat{z}^{l+1})) + \hat{z}^{l+1} \\ \end{aligned} z^lzlz^l+1zl+1=W_MSA(LN(zl−1))+zl−1=MLP(LN(z^l))+z^l=SW_MSA(LN(zl))+zl=MLP(LN(z^l+1))+z^l+1
3.2.3 Efficient batch computation for shifted configuration
shifted window划分方式会引入了另外一个问题,就是会产生更多的windows,也就是两个block之间的窗口不匹配问题,并且其中一部分window会比MxM(4x4)要小。
一个简单的解决方案是,在计算注意力时将较小的窗口填充到M×M大小,并屏蔽填充值。当常规分区中的窗口数量很小时,例如2×2,这种朴素解增加的计算量是相当大的(2×2→3×3,是原来的2.25倍,也就是需要填充2.25倍)。
随后,作者提出了另外的一种方法,更高效的批处理计算方法,通过向左上方向循环移动,如图4所示:

在这种移位之后,一个批处理窗口可能由几个在特征映射中不相邻的子窗口组成,因此使用掩蔽机制将自注意计算限制在每个子窗口内。通过循环移位,批处理窗口(batched window)的数量与常规窗口(regular window)分区的数量保持一致,因此也是高效的。
这里不太好理解,原话为:After this shift, a batched window may be composed of several sub-windows that are not adjacent in the feature map, so a masking mechanism is employed to limit self-attention computation to within each sub-window.
按我的理解就是对于regular window的窗口是2x2的,而对于batched window是3x3的,那么这3x3的窗口可以循环移动4次表示为2x2的窗口数量,在这个过程中将一些子窗口进行合并成一个,这样操作后regular window与batched window的计算量就一致了
对于Swin Transformer的结构目前只能有一个大概的了解,细节部分还需要看原来来查看具体的实现方式。
4. Result
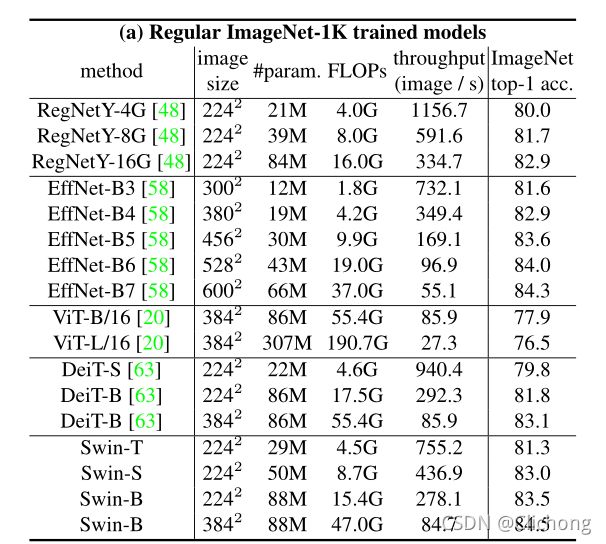
- 常规ImageNet-1K训练模型比较:
- ImageNet-22K pre-trained模型比较

- 目标检测与其他模型的对比结果:


- 语义分割的对比结果:
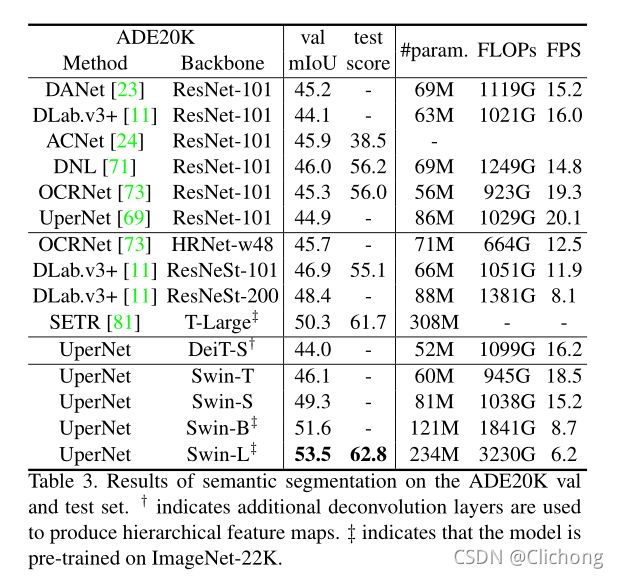
综上可以看出,使用Swin Transformer作为各种计算机视觉任务的backbone都达到了SOTA的效果。
总结:
作者在Swin Transformer中入 CNN 中常用的层次化堆叠方式(即金字塔结构)构建分层 Transformer,并且引入局部性(locality)思想,对不重叠的窗口区域内进行自注意力计算,来降低计算复杂度。而对于局部化带来的信息交互少的问题,提出移动窗口(shifted window)来解决。