LeetCode42——接雨水——DP or Two Pointers

这是一道面试常考题，题面如下：

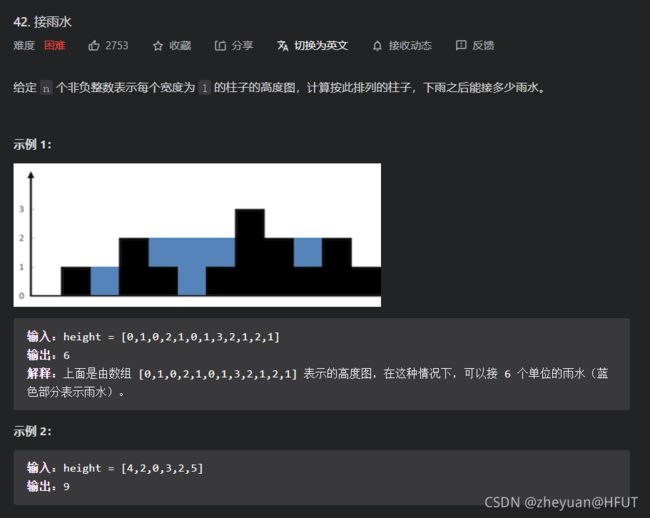
意思就是在给出了数组之中，数组中的每一个元素都是代表了一个模板的长度，求这些木板围起来的空间所能容纳的水的体积。这道题官方题解给了三种方法：动态规划、单调栈和双指针。这里只把动态规划和双指针的解法记录下来。

1.动态规划
首先要发现一个规律，这个规律至关重要：一块木板上所能积蓄的水量 = min(这个木板以左的最高木板(含自身)，这个木板以右的最高木板(含自身)) - 木板本身的高度，注意所谓以左以右的高度要包含自身，如果不包含会算出错误结果。如果不包含，那么假设有一序列为1，2，3，三这个位置记录的值将会是2而非自身3，而事实上长度为2的模板无法作为3的左边界，水会漏出。

发现了上面的公式，剩下的就是求每一个木板对应的左右最高木板数组了，这个数组可以使用DP来求。以LeftMaxHeight数组为例，会有转移方程LeftMaxHeight[i] = max(LeftMaxHeight[i - 1] + height[i])
，两趟DP分别求出所有木板左右两端木板(含自身)的最大值，这是一个很简单的DP：

		int Length = height.size();

        /*using DP to get the left max height and right max height*/
        int* LeftMaxHeight = new int [Length];
        int* RightMaxHeight = new int [Length];

        /*initialize*/
        LeftMaxHeight[0] = height[0];
        RightMaxHeight[Length - 1] = height[Length - 1];

        /*left to right ->, search for the left max height*/
        for(int i = 1 ; i < Length ; ++i)
            LeftMaxHeight[i] = max(LeftMaxHeight[i - 1], height[i]);
        
        /*right to left <-, search for the right max height*/
        for(int j = Length - 2 ; j >= 0 ; --j)
            RightMaxHeight[j] = max(RightMaxHeight[j + 1], height[j]);

随后根据DP求得的数组来进行问题的求解即可，用的就是上面那个重要规律：

		int Ans = 0; // answer
        for(int i = 1 ; i < Length - 1 ; ++i)
            Ans += (min(LeftMaxHeight[i], RightMaxHeight[i]) - height[i]);

这就是此题的动态规划解法。

2.双指针
动态规划的解法相对简单，但是需要遍历height数组三次，时间成本上不划算。双指针法只需要遍历height数组一次，不过这种方法思考起来可能难度更大，但是原理和动态规划是一致的。在这种解法中使用两个变量来记录从左向右或从右向左的木板高度最大值，分别记为LeftMax和RightMax，进而避免了像DP那样开辟两个数组重复记录，代码如下：

		int Length = height.size();

        int Head = 0, Tail = height.size() - 1;
        int Ans = 0;
        int LeftMax = 0, RightMax = 0;

        while(Head != Tail)			/*循环终止的条件是两个指针相遇*/
        {
     
            LeftMax = max(height[Head], LeftMax);
            RightMax = max(height[Tail], RightMax);

            if(LeftMax < RightMax)
            {
     
                Ans += (LeftMax - height[Head]);
                ++Head;
            }
            else
            {
     
                Ans += (RightMax - height[Tail]);
                --Tail;
            }
        }

        return Ans;