- 树的定义及其概念
- 树的父亲表示法
- 树的孩子兄弟表示法
- 二叉树
- 满二叉树
- 完全二叉树
- 二叉树的遍历
- 深度优先遍历
- 广度优先遍历
- 先序遍历/前序遍历
- 中序遍历
- 后序遍历
- 先序遍历,中序遍历,后序遍历的应用
树的定义及其概念
什么是树?
(图片源自网络)
差不多了
我们给他加工一下
去掉大量树叶抽取主干树枝

倒立并美化一下
就变成了一棵树
(美化完还是好丑啊)
我们可以发现原来的“树根”到了上面,因为我给他倒立了。
然后从树根可以扩散出主干,每条主干又可以扩散出几条分支,分支又可以扩散出分支……最后不能扩散的分支连接的就是叶子。
如果我们让树根是第一层(你喜欢的话第零层也可以),那么所有和树根直接相连的点就是第二层。
除了树根之外所有和第二层相连的点构成第三层。
除了第二层的点之外所有和第三层相连的点构成第四层(我诚实我没画出来)
……
所以你就可以发现,除了第\(n-1\)层的点之外所有和第\(n\)层连接的点构成第\(n+1\)层
这就是树的基本定义(反正又不考这么简单的概念自己理解记忆就好了)
树还有一些专有名词。
比如说刚刚提到的树根
你会发现,在树中任意一个结点(就是那个圈)都可以作为树根,按照上面的关系确定各个结点对应的层,就可以构成一棵树。所以说一棵无根树(是指没有指定根的树,不是没有根的树)的形态不是固定的
我们现在选定一个结点为根,然后确定每个结点的层数
树根一般会叫做第一层,有时也会叫做第零层。本文中采用第一种。
我们规定和这个结点直接相连的,层数比这个结点大1的所有结点叫做当前结点的儿子。
那么对应的当前结点就是这些结点的父亲。
比如:
- 树根是所有第二层的点的父亲。
- 第二层的点的父亲是树根。
- 第二层的点是树根的儿子。
- 树根的儿子是第二层的所有点。
树的深度,就是树的层数。如果树最深那一层是第\(n\)层,那么树的深度就是n(根节点是第1层)。如果根节点是第0层,那么深度就应该是\(n+1\)
我们又可以发现,对于树中任意一个点,他的儿子数量不是确定的。可以没有(叶子结点),可以有一个,可以有两个,可以有很多个。
然而除了树根之外,所有结点都有且只有唯一一个确定的父亲。根结点没有父亲。
然后一棵树中每个点肯定都有一条连向父亲的边,除了根结点没有父亲。
所以一棵有\(n\)个点树里面有\(n-1\)条“树枝”,也就是边
反过来也是成立的,一个有\(n\)个点\(n-1\)条边的连通图一定是一棵树,满足每个点有且只有一个父亲的性质(除了树根)。
又因为树根可以任意取,所以做题的时候一般以1号结点作为树根。(题目有特殊说明就看题目)
树的父亲表示法
如果我们用一个数组\(fa_i\)来表示结点\(i\)的父亲
然后为了方便我们令\(\forall 0
为什么要这样方便定义?因为我们没有存储儿子的信息,想要找到儿子就只能一个个遍历,每次都要遍历n个结点,很不爽。所以我们索性让儿子的索引号一定排在父亲后面,每次从父亲开始搜索,搜到\(fa_j=i\)就可以说明结点j是i的儿子。
个人觉得这种方法很不爽
所以我要超纲
树的孩子兄弟表示法
上面的方法太浪费时间了。
我们可以发现一旦一棵树的形态确定了下来,那么父亲的儿子就确定了
我们要保存这个节点的儿子,因为题目经常这样搞
但是每个节点的儿子数量是不一定的,我们如果统一开数组。。。很浪费空间。
我们参考一下链表
我们可以发现,父节点可以只保存第一个儿子的信息,然后让第一个儿子保存第二个儿子的信息,第二个保存第三个……
那么每个节点只需要保存:我的下一个兄弟,我的第一个儿子
空间上变成了两倍,但是时间上快了很多很多
(质的飞越)
这就是大名鼎鼎的链式前向星
struct Edge
{
/*
这里用边来表示指向的节点
@param: int v 这条边指向的节点的编号
int u 指向下一个儿子的边的编号(可以找到下一个兄弟)
*/
int u,v;
};
// 用来表示节点的第一个儿子,具体大小按需要自定
int head[];
void add(int a,int b)
{
/*
用来增加一条从a连向b的边,即a是b的父亲
@param: int a 父亲 int b 儿子
@return: void
*/
static int tot=0; // 表示使用这个函数加的边的总数,那么这个tot+1就是新边的编号了
edge[++tot]=(Edge){head[a],b}; // 新的边指向b,下一个(上一个?差不多啦反正能找到所有的兄弟就可以了)兄弟的边的编号
head[a]=tot; // 更新a的第一个儿子为b,也就是指向b的边,也就是新的边,就是更新后的tot
}
我们在加边的时候要注意只能是父亲连向儿子,不能儿子逆向连回父亲。
光说不做总不好,我们用题来说话
很明显,城堡是无根树,我们就令根为1
然后建树(主要理解这个步骤)
然后树上dp
设\(f_{i,j}\)表示在\(i\)节点放\((j=1)\)或不放\((j=0)\)时,这棵子树满足所有边都被看见的最小需要的士兵数量。
子树是什么……额……对于一棵树,任意一个节点和他的后代(儿子,儿子的儿子,儿子的儿子的儿子……)所构成的数(也一定是一棵树)叫做子树,这个节点叫做子树的根。跟子集是差不多的概念。但子树一般默认是非空真子树。
很明显,如果\(i\)是叶子节点,那么子树\(i\)(以\(i\)为根的子树)只有\(i\)一个节点,没有边,所以
\(f_{i,0}=f_{i,1}=0\),并不需要士兵。这也是递归的初始条件。
我们再来想想递推的结束条件,应该是整棵树满足条件所需要的最小士兵数量,也就是根为\(1\)的子树的\(f\),即
\(\min(f_{1,0},f_{1,1})\),所需要的士兵就是整棵树满足条件所需要的最小士兵数,也就是递推边界
(不知道你们怎么理解反正我觉得动态规划就是递推)
然后再来想想状态转移方程
对于一个节点\(i\),如果是叶子结点,按照上面方式初始化。如果不是叶子结点,那么我们就分类讨论:
- 这个节点放置士兵
那么他的儿子放不放士兵都随便,看怎样便宜怎样来。 - 这个节点不放置士兵
那么他的所有儿子都必须放置士兵,代价(花费)就是所以儿子放置士兵,所有以儿子为根的子树都满足性质的最小代价和
写成方程就长这样:
然后我们来讨论一下建树
首先用链式前向星存双向边,然后用dfs初始化,处理出每个节点的父亲。如果这条边是指向父亲的话就跳过或者直接删除这条边。否则这条边就是指向儿子的
然后就。。。不停递推
#include
using namespace std;
struct Edge
{
int u,v;
}edge[3000]; // 有1500个点,1499条边,建双向边就需要开3000数组
int head[1500]; // 储存每个节点连出去的第一条边(第一个儿子
int n,fa[1500],a,b,k;
int dp[1500][2];
void add(int a,int b)
{
/*
增加一条单向边
@param: int a 单向边的起点
int b 单向边的终点
@return: void
*/
static int tot=0;
edge[++tot]=(Edge){head[a],b}; head[a]=tot;
}
void init(int k,int f)
{
/*
处理一个结点
@param: int k 当前要处理的结点
int f 这个结点的父亲
@return: void
*/
fa[k]=f;
dp[k][0]=0; dp[k][1]=1; // 初始化,叶子结点不会执行下面的循环
for(int j=head[k];j;j=edge[j].u)
{
if(edge[j].v==fa[k]) continue;
init(edge[j].v,k); // 指向的不是父亲,先处理这个儿子,然后再维护自己
dp[k][0]+=dp[edge[j].v][1];
dp[k][1]+=std::min(dp[edge[j].v][0],dp[edge[j].v][1]);
}
}
int main()
{
std::cin>>n;
for(int i=1;i<=n;++i)
{
std::cin>>a>>k;
while(k--)
{
std::cin>>b;
add(a,b);
add(b,a); // 建立双向边,正着反着都调用一次
}
}
init(1,-1);
std::cout< 这里init函数是跳过版本的。如果需要调用的情况比较多,可以考虑把指向父亲的边删掉。
比如这样,通过链表的删除全部的方法删除。
void init(int k,int f)
{
/*
处理一个结点
@param: int k 当前要处理的结点
int f 这个结点的父亲
@return: void
*/
fa[k]=f;
dp[k][0]=0; dp[k][1]=1; // 初始化,叶子结点不会执行下面的循环
while(edge[head[k]].v==fa[k]) head[k]=edge[head[k]].u;
for(int j=head[k];j;j=edge[j].u) // 从第一条边开始遍历所有的边。便利到最后j是0就表示遍历完了退出循环。
{
while(edge[edge[j].u].v==fa[k]) edge[j].u=edge[edge[j].u].u;
init(edge[j].v,k); // 指向的不是父亲,先处理这个儿子,然后再维护自己
dp[k][0]+=dp[edge[j].v][1];
dp[k][1]+=std::min(dp[edge[j].v][0],dp[edge[j].v][1]);
}
}
但是你会发现用在这道题上面是TLE的
这是因为这道题有0号结点。有些结点的父亲就是0,然而如果这条边是0号边也就是不存在,这个边指向的点也是0,就会在while里面往复
所以我们加一个维护
void init(int k,int f)
{
/*
处理一个结点
@param: int k 当前要处理的结点
int f 这个结点的父亲
@return: void
*/
fa[k]=f;
dp[k][0]=0; dp[k][1]=1; // 初始化,叶子结点不会执行下面的循环
while(edge[head[k]].v==fa[k]&&head[k]) head[k]=edge[head[k]].u;
for(int j=head[k];j;j=edge[j].u)
{
while(edge[edge[j].u].v==fa[k]&&edge[j].u) edge[j].u=edge[edge[j].u].u;
init(edge[j].v,k); // 指向的不是父亲,先处理这个儿子,然后再维护自己
dp[k][0]+=dp[edge[j].v][1];
dp[k][1]+=std::min(dp[edge[j].v][0],dp[edge[j].v][1]);
}
}
emmmm这里你听不懂没关系……反正是超纲的。
二叉树
我们再来看看这棵树
emmm不是这幅

如果我们类似图的定义来定义一下树的度
就会有:
结点的度:一个结点的儿子的数量
树的度:树中所有结点的度的最大值
所以上面是度为3的树
那么二叉树是什么呢?
就是一棵度为2的树
那么就会有,对于这棵二叉树中的任意一个结点,他儿子的数量不是0就是1或者2
既然这样,那我们干脆就叫任意一个结点的两个儿子分别为左儿子和右儿子(专业术语)
如果这个结点没有左儿子,就说左儿子为空
显然,叶子结点左右儿子都为空
二叉树会满足一些性质:
在根节点为第1层的情况下:
- 第\(i\)层最多有\(2^{i-1}\)个结点
- 深度为\(h\)的二叉树最多有\(2^{h}-1\)个结点
- 若在任意一棵二叉树中,有\(n_0\)个叶子节点,有\(n_2\)个度为2的节点,则必有\(n_0=n_2+1\)
证明:对于一棵二叉树,\(n_0,n_2\)的值都是由他的左右儿子决定的。
特殊地,如果这个结点没有左右儿子,那么就是叶子结点,\(n_0=1,n_2=0\),满足条件
当这个结点不是叶子结点的时候:
定义这个结点\(rt\)的子树分别为\(A,B\),且\(A,B\)如果不为空,则满足上述性质
当其中一个子树为空的时候,这里假设\(B\)为空,有\(rt_0=A_0,rt_2=A_2\),因为\(A\)满足性质,所以\(rt\)也满足性质
当两个子树都不为空的时候,有\(rt_0=A_0+B_0,rt_2=A_2+B_2+1\)(因为两个子树都不为空,\(rt\)也是一个度为2的结点)
\(rt_0=A_0+B_0=A_2+1+B_2+1=A_2+B_2+1+1=rt_2+1\)
所以无论\(rt\)是什么结点,叶子结点也好,不是叶子结点也好,他都满足性质。
所以当\(rt\)为根节点的时候,满足性质,表现为整棵二叉树满足性质。 - 具有\(n\)个结点的二叉树最小深度为\(\lfloor log_2n\rfloor+1\)
满二叉树
对于所有非叶子结点度都为2,且叶子结点都在同一层的二叉树,我们叫做满二叉树(在不增加层数的情况下你插入不了结点了,就是满了)
百度定义:满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
然后我们可以给满二叉树的结点编号
一层一层编下来。
首先
第一层根节点给1
第二层只有两个节点,一个是1的左儿子,一个是1的右儿子。分别给2和3
第三层有四个结点,分别是2的左右儿子,3的左右儿子。对于2的左儿子按照顺序给4,右儿子给5。3的左儿子6,右儿子7
。。。。。。
第\(i\)层有\(2^{i-1}\)个结点,他们的编号分别是\(2^{i-1},2^{i-1}+1\dots 2^{i}-1\)
这个方法叫做顺序编号。就是先按照层的顺序,再按照层中从左到右的顺序给结点进行编号。
然后根据推理(反正我推不出来)观察,发现,对于编号为\(j\)的非叶子结点,它的左儿子编号为\(2j\),右儿子编号为\(2j+1\)
在C++中可以使用位运算符来加快运算速度
j<<1; // 等价于j*2
j<<1|1; // 等价于j*2+1
完全二叉树
是一棵残缺的满二叉树,但是满足顺序编号所有的结点在与满二叉树中对应的结点编号相同。
我觉得百度讲的比我清楚qwq
二叉树的遍历
遍历,就是按照一定顺序输出二叉树的结点所储存的信息而不是编号
首先插播一条超纲知识:
对于所有的树(所有的图,树是一种特殊的图),我们可以采用以下两种遍历方式:
深度优先遍历
就是一路dfs深搜下去,每搜索到一个结点就输出信息并标记已访问(树不会重复访问结点所以不用标记)。搜到叶子结点就返回,否则就dfs他的所有儿子
这种遍历方法输出的特点是同一子树内的结点会在一起被遍历到(如果你保存到数组里就是保存在连续的一段)
写成代码长成这样
void dfs(int k)
{
/*
深度优先遍历
@param: int k 当前遍历到的结点编号
@return: void
*/
print(val[k]); // 用专门的输出函数来输出这个结点的数据(如果是普通数据可以直接输出,不必调用函数)
static int tot=0;
dat[++tot]=val[k]; // 保存到数组
for(int j=head[i];j;j=edge[j].u) // 链式前向星遍历儿子
{
// 如果访问过就跳过,这里vis是定义在一些神奇的地方(函数外啊,函数内啊随便。反正我没定义(逃)。。。)
if(vis[edge[j].v]) continue; // 图的写法,树可以改成if(edge[j].v==fa[k])
dfs(edge[j].v); // 没有访问过,就遍历
}
}
广度优先遍历
顾名思义就是用广度优先搜索算法遍历的,也叫做层次遍历/层序遍历(随便叫吧)
用queue的bfs实现的。每次从队头拿出一个结点,输出信息并标记访问(树不会重复访问所以不用标记),然后把这个结点的所有儿子都放进队列中。重复执行直到队列为空。
这种遍历方法输出的特点是同一层的结点会在一起被遍历到(如果保存到数组就是保存在连续的一段。)
void bfs(int rt)
{
/*
广度优先遍历
@param: int rt 树的根
@return: void
*/
queue q;
q.push(rt); // 根节点入队
static int tot=0;
while(!q.empty())
{
int i=q.front(); q.pop(); // 取出队头结点
print(val[i]); // 输出
dat[++tot]=val[i]; // 保存
for(int j=head[i];j;j=edge[j].v) // 搜索所有儿子
{
if(vis[edge[j].v]) continue; // 访问过就跳过,图的写法,树可以改成if(edge[j].v==fa[k])
q.push(edge[j].v); // 没有访问过就入队
}
}
}
上面的遍历在二叉树中都可以用
现在来讲讲二叉树专有的遍历方式
首先给一棵来自百度百科的二叉树的图:
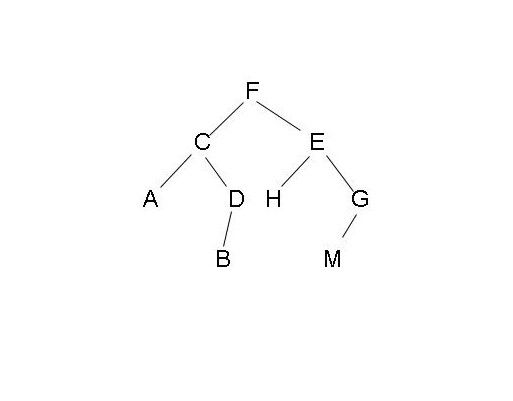
(如果图片显示不出来请复制上述网址粘贴到地址栏中查看)
这棵树的深度优先遍历可能是FCADBEHGM
广度优先遍历可能是FECGHADMB
具体取决于你建树时的细节操作和输出遍历时的操作
(也就是实现方法的不同会导致遍历结果的不同,但是一定满足遍历本身的性质)
但是接下来讲的三种遍历出来的序列是确定的:(因为你确定了左右儿子)
先序遍历/前序遍历
是基于深度优先遍历的遍历
每次遍历,先输出自己,然后输出左儿子的遍历序列,再输出右儿子的遍历序列
也就是遵循根左右原则
void dfs(int k)
{
/*
输出先序遍历
@param: int k 当前遍历到的结点
@return: void
*/
print(val[k]);
// 定义lson[k],rson[k]分别表示k的左右儿子
if(lson[k]) dfs(lson[k]); // 如果有左儿子才输出左儿子的先序遍历
if(rson[k]) dfs(rson[k]); // 如果有右儿子才输出右儿子的先序遍历
}
如上图,先序遍历是FCADBEHGM
中序遍历
是基于深度优先遍历的遍历
每次遍历,先输出左儿子的遍历序列,再输出自己,最后输出右儿子的遍历序列
也就是遵循左根右原则
void dfs(int k)
{
/*
输出中序遍历
@param: int k 当前遍历到的结点
@return: void
*/
if(lson[k]) dfs(lson[k]);
print(val[k]);
if(rson[k]) dfs(rson[k]);
}
如上图,中序遍历是ACBDFHEMG
后序遍历
是基于深度优先遍历的遍历
每次遍历,先输出左儿子的遍历序列,再输出右儿子的遍历序列,最后输出自己
也就是遵循左右根原则
void dfs(int k)
{
/*
输出后序遍历
@param: int k 当前遍历到的结点
@return: void
*/
if(lson[k]) dfs(lson[k]);
if(rson[k]) dfs(rson[k]);
print(val[k]);
}
如上图,后序遍历是ABDCHMGEF
先序遍历,中序遍历,后序遍历的应用
我们可以知道,对于确定的二叉树,它的这三种遍历的序列都是唯一的。
反过来不成立,对于确定的某个序列,二叉树的形态不是唯一的。
但是,如果有确定的先序遍历和中序遍历或者确定的中序遍历和后序遍历,就可以确定一棵二叉树的形态
但是只有先序遍历和后序遍历就不行,这个时候题目就会问你:中序遍历可能是,你只需要排除掉不可能的剩下的就是可能的了。
(至于为什么我也不知道)
改自2013腾讯笔试题:(不能复制。。。我手敲好累)
已知二叉树的先序遍历为FBACDEGH,中序遍历为ABDCEFGH,则后序遍历为
A: ADECBHGF
B: ABDECGHF
C: GHADECBF
D: HGADECBF
E(我自己加的): ABCDEF
首先这道题,有一个很白痴的问题(但是我一开始就跳进去了)
E是可以直接排掉的!!!
所以求可能的中序遍历的时候这也是一种要排除的选项。
(当时分析了好久)
然后我们看看这个先序遍历先
FBACDEGH
他告诉了我们什么
首先这个数有8个结点,非空(废话)。所以根据根左右原则,可以知道树根为F,那么BACDEGH就是左右子树的遍历序列。无论是哪个子树,无论形态长什么样,我们都可以知道B肯定是某个子树的根。
然后我们再看看中序遍历
ABDCEFGH
根节点F在中间,然后就由左根右知道F左边的ABDCE组成左子树的中序遍历序列,所以左子树由这5个结点组成(注意不是构成,现在还不知道具体形态),右子树由GH这2个结点组成
然后左子树的根是B,那么ABDCE又可以分成两段:A,DCE这时我们就知道,B的左儿子是A,右儿子是DCE组成的子树
那么这个右儿子是怎样的呢?
我们看看先序遍历中DCE的位置,是CDE,也就是C是根节点,那么DCE又被分成了两段:D,E所以C的左儿子是D,右儿子是E
那么ABDCE这棵左子树的形态我们就确定了
同样我们可以确定GH这棵右子树
先序遍历GH,中序遍历GH,所以G是根,H是右子树
综上,我们用(rt,A,B)表示一个结点\(rt\)的左子树\(A\),右子树\(B\)(对我懒得画图)
那么这棵树就可以表示成
(F,
(B, A, (C, D, E)),
(G, 0, H)
)
所以后序遍历就是ADECBHGF
所以选A
明白了吧?