Python - 动态规划之寻找并显示所有路径

一.引言

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

求可能的路径个数。

二.获取路径条数

1.动态规划

这是动态规划最基础的一个题目，转化到坐标系中，主要信息有两个:

A. 网格大小 M x N，起始点 (0,0) 终点 (m-1, n-1)

B. 每次只能向下或者向右移动，假设当前点 (k, j)，则下一步的坐标可能为 (k , j+1) 或者是 (k+1, j)

def uniquePaths(m, n):
    """
    :type m: int
    :type n: int
    :rtype: int
    """

    # 构建初始网格
    grid = [[0] * n for _ in range(m)]
    printMap(grid)

    # 初始化计数
    for i in range(m):
        grid[i][0] = 1
    for j in range(n):
        grid[0][j] = 1
    printMap(grid)

    for i in range(1, m):
        for j in range(1, n):
            left = up = 0
            up = grid[i - 1][j]
            left = grid[i][j - 1]
            grid[i][j] = left + up
            printMap(grid)
    return grid


m = 3
n = 7
result = uniquePaths(m, n)

2.代码分析

上面是主函数，主要分3个步骤:

A.构建初始网络

这一步主要初始化一个 M x N 的网格代表机器人  前进的地图

[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]

B.初始化计数

由于要求只能向下或者向右行进，所以针对最左边 (0, y) 和最上边 (x, 0) 的值都为1，因为到达所有位置的路线只有 1 条

[1, 1, 1, 1, 1, 1, 1]
[1, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0, 0]

C.遍历累加

对除了 (0, y) 和 (x , 0) 的点进行状态累加，对于位置 (1, 1) 从起始点到其位置可能性有两种，一种是 (0, 1) -> (1, 1) 或者是 (1, 0) -> (1, 1) ，所以 v(1, 1) = 1 + 1 = 2 ，即左侧和上面的可能性之后，之后的点以此类推，这里把整个规划问题分成若干个局部小问题解决。最后 (m-1, n-1) 的数值代表所有的可能性。

========================
[1, 1, 1, 1, 1, 1, 1]
[1, 2, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0, 0]
========================
[1, 1, 1, 1, 1, 1, 1]
[1, 2, 3, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0, 0]
========================
[1, 1, 1, 1, 1, 1, 1]
[1, 2, 3, 4, 0, 0, 0]
[1, 0, 0, 0, 0, 0, 0]
========================
......
========================
[1, 1, 1, 1, 1, 1, 1]
[1, 2, 3, 4, 5, 6, 7]
[1, 3, 6, 10, 15, 0, 0]
========================
[1, 1, 1, 1, 1, 1, 1]
[1, 2, 3, 4, 5, 6, 7]
[1, 3, 6, 10, 15, 21, 0]
========================
[1, 1, 1, 1, 1, 1, 1]
[1, 2, 3, 4, 5, 6, 7]
[1, 3, 6, 10, 15, 21, 28]
========================

def printMap(m):
    for line in m:
        print(line)
    print("========================")

辅助函数负责把网格打出来，可以看到完整的过程。

三.获取路径坐标

上面通过动态规划的方法，可以获得起点到终点路线方案总和，但是不能只管的看到路径的走向，下面通过决策树方法遍历的到所有路径。

1.构造决策树

对于每一个点，他都有 0-2 种可能， 0 对应终点，1 对应下边界， 2 对应其他点，从起点 (0, 0) 开始，依次递归，最终到达 (m-1, n-1) 的终点。对于这样发散延伸的结构，适合树结构，所以除了使用动态规划的方法，可以使用树，不仅可以求路径总数，也可以获取全部路径坐标。

A.获取每个点的下一步

col_bound = n - 1
row_bound = m - 1
start = "0_0"
end = changeIndex(row_bound, col_bound)
print("start: %s end: %s" % (start, end))


def getAllPossibility():
    possibility = {}

    print("Col 边界: %s Row 边界: %s" % (col_bound, row_bound))

    for i in range(0, m):
        for j in range(0, n):
            cur_index = "%d_%d" % (i, j)
            possibility[cur_index] = []
            if (i + 1) <= row_bound and j <= col_bound:
                possibility[cur_index].append(changeIndex(i + 1, j))
            if i <= row_bound and (j + 1) <= col_bound:
                possibility[cur_index].append(changeIndex(i, j + 1))

    return possibility


# 获取全部情况
allPossibility = getAllPossibility()

根据上面最后的结果图，可以遍历出来每个点可以走的点位，终点 (m-1, n-1) 的 List 为空 ，这里 

changeIndex 就是把 row，col 通过 _ 拼接起来:

def changeIndex(_i, _j):
    return "%d_%d" % (_i, _j)

{'0_0': ['1_0', '0_1'], '0_1': ['1_1', '0_2'], '0_2': ['1_2', '0_3'], 
'0_3': ['1_3', '0_4'], '0_4': ['1_4', '0_5'], '0_5': ['1_5', '0_6'], 
'0_6': ['1_6'], '1_0': ['2_0', '1_1'], '1_1': ['2_1', '1_2'], 
'1_2': ['2_2', '1_3'], '1_3': ['2_3', '1_4'], '1_4': ['2_4', '1_5'],
'1_5': ['2_5', '1_6'], '1_6': ['2_6'], '2_0': ['2_1'], '2_1': ['2_2'], 
'2_2': ['2_3'], '2_3': ['2_4'], '2_4': ['2_5'], '2_5': ['2_6'], '2_6': []}

B.生成决策树

通过上面的 dict 可以递归生成决策树，根据列表 [] 的长度判断向左还是向右递归，有需要可以在 BitNode 逻辑中加入前序，中序，后续遍历的逻辑，前面也给到过: 遍历决策树https://blog.csdn.net/BIT_666/article/details/118222309?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163550588716780264063245%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=163550588716780264063245&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_v2~rank_v29-1-118222309.pc_v2_rank_blog_default&utm_term=dfs&spm=1018.2226.3001.4450https://blog.csdn.net/BIT_666/article/details/118222309?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163550588716780264063245%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=163550588716780264063245&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_v2~rank_v29-1-118222309.pc_v2_rank_blog_default&utm_term=dfs&spm=1018.2226.3001.4450

# 构建二叉树类
class BitNode:
    def __init__(self):
        self.data = None
        self.left = None
        self.right = None


def map2tree(pro, root_data, leap_data):
    data = pro[root_data]
    length = len(data)
    if length != 0:
        _root = BitNode()
        _root.data = root_data
        if length == 1:
            _root.left = map2tree(pro, data[0], leap_data)
        else:
            _root.left = map2tree(pro, data[0], leap_data)
            _root.right = map2tree(pro, data[1], leap_data)
    else:
        _root = BitNode()
        _root.data = leap_data
    return _root


# 获取决策树
root = map2tree(allPossibility, start, end)

2.获取根节点到每个叶节点的路径

决策树的基本操作，继续使用递归实现，concatPath 方法不断累加路径长度并递归，直到终点达到递归退出条件随后将完整路径添加至 all_path

all_path = []


# 获取一棵树顶点到每个叶节点的路径
def getPath(_root):
    if _root.left is None and _root.right is None:
        all_path.append(_root.data)
    else:
        if _root.left is not None:
            concatPath(_root.left, _root.data)
        if _root.right is not None:
            concatPath(_root.right, _root.data)


def concatPath(_root, data):
    if _root.left is None and _root.right is None:
        all_path.append(data + "->" + _root.data)
        return
    else:
        if _root.left is not None:
            concatPath(_root.left, data + "->" + _root.data)
        if _root.right is not None:
            concatPath(_root.right, data + "->" + _root.data)


# 获取全部路径
getPath(root)

0_0->1_0->2_0->2_1->2_2->2_3->2_4->2_5->2_6
0_0->1_0->1_1->2_1->2_2->2_3->2_4->2_5->2_6
0_0->1_0->1_1->1_2->2_2->2_3->2_4->2_5->2_6
0_0->1_0->1_1->1_2->1_3->2_3->2_4->2_5->2_6
......
0_0->0_1->0_2->0_3->0_4->1_4->1_5->1_6->2_6
0_0->0_1->0_2->0_3->0_4->0_5->1_5->2_5->2_6
0_0->0_1->0_2->0_3->0_4->0_5->1_5->1_6->2_6
0_0->0_1->0_2->0_3->0_4->0_5->0_6->1_6->2_6

Total Path Num: 28

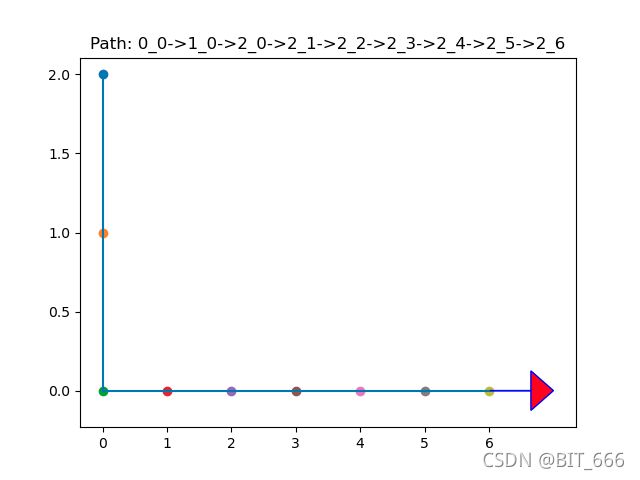
四.绘制路线图

本来上面拿到全部路径就够了，心想还是不够完美，如果是一个完整的项目需求，除了线路坐标，如果能够给出真实的线路图那就更好了，所以接下来使用 matplotlib 把所有路径简单展示一下。

def plotPathMap(path):
    points = list(map(lambda point: point.split("_"), path.split("->")))
    lines = [[], []]
    for row, col in points:
        change_row = col
        change_col = int(row_bound) - int(row)
        lines[0].append(change_row)
        lines[1].append(change_col)
        plt.scatter(change_row, change_col)
    plt.plot(lines[0], lines[1])
    plt.title("Path: " + path)
    plt.arrow(col_bound, 0, 1, 0, length_includes_head=True, head_width=0.25, head_length=0.35, fc='r', ec='b')
    plt.show()


for path in all_path:
    print(path)
    plotPathMap(path)
print("Total Path Num: %d" % len(all_path))

由于原始坐标系和 matplotlib 的坐标系是中心对称且上下颠倒的的，所以得到的坐标需要经过转换才能还原到图布中，当然如果不想转换坐标系，也可以讲题目修改为机器人在左下角，目标点在右上角。为了表示方向，这里使用了 arrow 增加了箭头指向。

 ...... 

五.总结

上面大概是基本的动态回归和树相关的实现，有更好的实现思路和方法可以一起进步！