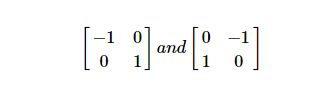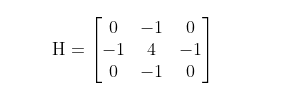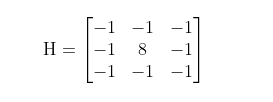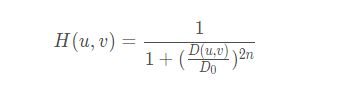OpenCv图像锐化及各种高通滤波
目录
什么是图像锐化以及为什么要进行图像锐化
图像锐化的方法
1.空域滤波的可使用几种方法
1.1梯度法
1.2拉普拉斯算子法
1.3定向滤波法
2.频域方面的高通滤波
2.1理想高通滤波器
2.2巴特沃斯高通滤波器
什么是图像锐化以及为什么要进行图像锐化
是什么?
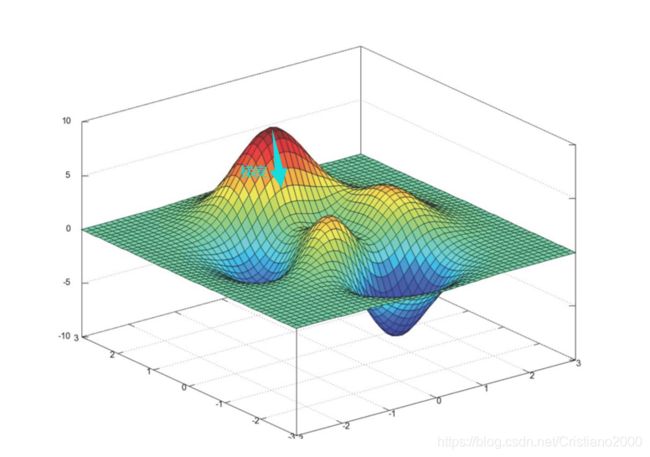
消除或减弱图像的低频分量从而增强图像中物体的边缘轮廓信息的过程称为图像锐化。
为什么?
在上一节图像平滑处理过程中不仅消除了噪音,也使边缘纹理受到了损失(都是高频分量)。为了突出图像的边缘纹理信息,就可以使用图像锐化处理。
图像锐化的方法
图像锐化可以采用基于空间域的空域滤波的几种锐化方法或者基于频率域的高通滤波来处理。
1.空域滤波的可使用几种方法
1.1梯度法
也称一阶导数法。
①梯度的含义:
梯度的方向是方向导数取得最大值的方向,梯度的大小是方向导数的最大值。
方向导数是函数沿着某一方向的导数。(一般在3维函数上理解)
导数是函数在某一点的变化率。(一般在2维函数上理解)
那么,以上三个概念叠加起来再结合图像后可以简单理解为对于图像某一像素点而言,梯度就是其值变化最快的方向向量。
②罗伯特(Robert)梯度算子
——《数字图像处理》第2版,陈天华编著
简单来说,对于一个像素点的值,用周围4个值交叉相减的绝对值之和代替。
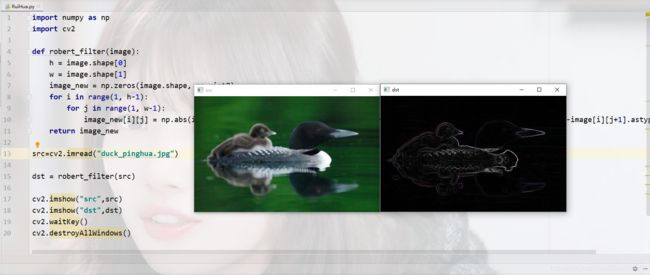
③程序演示,基于Python Opencv
*注意:图片的数据类型一般是uint8,两个uint8的数据相加减经常出现标量溢出的情况,可以使用astype()函数转化为int后再进行运算。
1.自定义方法
###################
# Robert算子 #
###################
def robert_filter(image):
h = image.shape[0]
w = image.shape[1]
image_new = np.zeros(image.shape, np.uint8)
for i in range(1, h-1):
for j in range(1, w-1):
image_new[i][j] = np.abs(image[i][j].astype(int)-image[i+1][j+1].astype(int)) + np.abs(image[i+1][j].astype(int)-image[i][j+1].astype(int))
return image_new2.上篇我们提到的自定义滤波器(cv::filter2D())来实现。
制作Robert交叉算子内核(模板):
kernel_1 = np.array([[-1, 0], [0, 1]], dtype=int)
kernel_2 = np.array([[0, -1], [1, 0]], dtype=int)
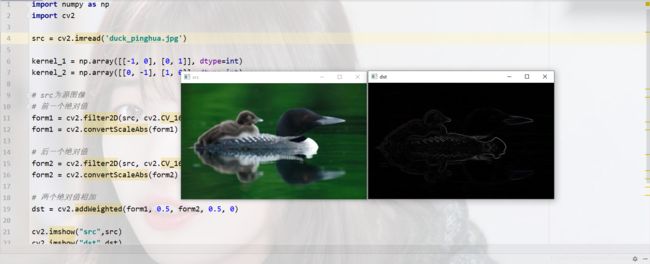
# src为源图像
# 前一个绝对值
form1 = cv2.filter2D(src, cv2.CV_16S, kernel_1)
form1 = cv2.convertScaleAbs(form1)
# 后一个绝对值
form2 = cv2.filter2D(src, cv2.CV_16S, kernel_2)
form2 = cv2.convertScaleAbs(form2)
# 两个绝对值相加,得到目标图像dst
dst = cv2.addWeighted(form1, 0.5, form2, 0.5, 0)1.2拉普拉斯算子法
①数学原理:
②程序实现,基于Python Opencv:
跟上一小节一样要么自己定义方法要么使用模板结合filter2D()
1.自定义方法
def laplacian_filter(image):
h = image.shape[0]
w = image.shape[1]
image_new = np.zeros(image.shape, np.uint8)
for i in range(1, h-1):
for j in range(1, w-1):
image_new[i][j] = 4*image[i][j].astype(int) - image[i + 1][j].astype(int) - image[i - 1][j].astype(int) - image[i][j + 1].astype(int) - image[i][j - 1].astype(int)
return image_new2.使用cv::filter()
拉普拉斯算子模板:
另外再提一下,还可以使用8邻域模板。
# 4邻域模板与8邻域模板
kernel_4 = np.array([[0, -1, 0], [-1, 4, -1], [0, -1, 0]], dtype=int)
kernel_8 = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype=int)
# src为源图像
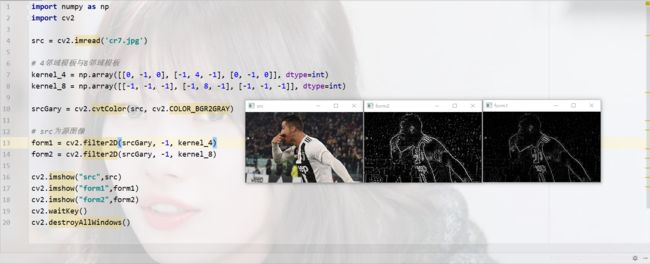
form1 = cv2.filter2D(src, cv2.CV_16S, kernel_4)
form2 = cv2.filter2D(src, cv2.CV_16S, kernel_8)1.3定向滤波法
顾名思义,定向滤波是一种定向锐化的模板,可以对一定方向的物体行迹进行锐化突出
比如河流的走向是从左下角走向右上角,因此可以突出锐化对角方向。
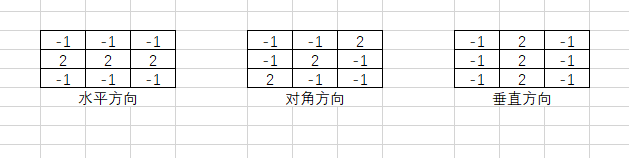
①常用的三种定向滤波模板
②程序实现,基于Python Opencv:
kernel_shuiping = np.array([[-1, -1, -1], [2, 2, 2], [-1, -1, -1]], dtype=int)
kernel_duijiao = np.array([[-1, -1, 2], [-1, 2, -1], [2, -1, -1]], dtype=int)
kernel_chuizhi = np.array([[-1, 2, -1], [-1, 2, -1], [-1, 2, -1]], dtype=int)
# src为源图像
shuiping = cv2.filter2D(src, -1, kernel_shuiping)
duijiao = cv2.filter2D(src, -1, kernel_duijiao)
chuizhi = cv2.filter2D(src, -1, kernel_chuizhi)2.频域方面的高通滤波
学习基于频域方面的高通滤波,那就要先学习频域变换,也就是学习傅里叶变换。
关于频域与傅里叶变换:
假如我们的图像是f(x,y),经过与算子(也称模板)h(x,y) 进行卷积运算后,得到一张原图像中某些特征被强化的新图像g(x,y)。
描述上述这句话的公式是:g(x,y)=f(x,y)*h(x,y)
而这个公式在频域中表示G(x,y)=F(x,y)H(x,y)。G、F、H分别是g、f、h的傅里叶变换。
那么以上帝视角来说,已知f,为了得到g,我们先将f变换为F,再构造滤波器函数H,就可以得到G,最终将G变换回g。
值得注意的是:
在操作时,图片刚被变换到频域时,低频集中在一起出现在左上角,为了操作方便,需要将其移到中心。也正是因为这一点,低通滤波器可以制作掩膜屏蔽中心外的即屏蔽高频;高通滤波器可以制作掩膜屏蔽靠近中心的即屏蔽低频。
另外,傅里叶逆变换回来后,是矢量图,需要转换为标量。
下面来详细介绍几种常见的高通滤波器。
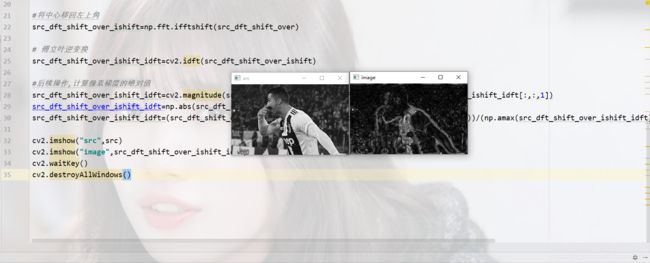
2.1理想高通滤波器
顾名思义,非常理想,直接果断地屏蔽中心低频留下外围高频。
import cv2
import numpy as np
# 以灰度图读出图片
src=cv2.imread('cr7.jpg',0)
# 傅立叶变化
src_dft=cv2.dft(np.float32(src),flags=cv2.DFT_COMPLEX_OUTPUT)
# 将图片中心从左上角移到中心
src_dft_shift=np.fft.fftshift(src_dft)
# 制作掩膜令中心为0,后面才能过滤掉中心低频
rows,cols=src.shape
crow,ccol=int(rows/2),int(cols/2)
mask=np.ones((rows,cols,2),np.uint8)
mask[crow-10:crow+10,ccol-10:ccol+10]=0
# 用掩膜对图像进行处理
src_dft_shift_over=src_dft_shift*mask
#将中心移回左上角
src_dft_shift_over_ishift=np.fft.ifftshift(src_dft_shift_over)
# 傅立叶逆变换
src_dft_shift_over_ishift_idft=cv2.idft(src_dft_shift_over_ishift)
#后续操作,将矢量转换成标量,并映射到合理范围之内
src_dft_shift_over_ishift_idft=cv2.magnitude(src_dft_shift_over_ishift_idft[:,:,0],src_dft_shift_over_ishift_idft[:,:,1])
src_dft_shift_over_ishift_idft=np.abs(src_dft_shift_over_ishift_idft)
src_dft_shift_over_ishift_idft=(src_dft_shift_over_ishift_idft-np.amin(src_dft_shift_over_ishift_idft))/(np.amax(src_dft_shift_over_ishift_idft)-np.amin(src_dft_shift_over_ishift_idft))
cv2.imshow("src",src)
cv2.imshow("image",src_dft_shift_over_ishift_idft)
cv2.waitKey()
cv2.destroyAllWindows()2.2巴特沃斯高通滤波器
①数学理论:
传递函数H为:
D(u,v)是指点到频域原点的距离。
n为滤波器的阶次。
D0为滤波器的截至频率。一般取D(u,v)最大值的0.5(1/2)或0.707(√2/2)。
②基于Opencv的程序实现:
import cv2
import numpy as np
# 以灰度图读出图片
src=cv2.imread('nqm2.jpg',0)
# 傅立叶变化
src_dft=cv2.dft(np.float32(src),flags=cv2.DFT_COMPLEX_OUTPUT)
# 将图片中心从左上角移到中心
src_dft_shift=np.fft.fftshift(src_dft)
# 制作掩膜,由于计算需要,我们先制作单通道的。
rows,cols=src.shape
crow,ccol=int(rows/2),int(cols/2)
mask=np.zeros((rows,cols),np.float64)
# 先计算点到中心的距离即公式中的D(u,v)
for i in range(rows):
for j in range(cols):
mask[i,j] = np.sqrt((i-crow) * (i-crow) + (j-ccol) * (j-ccol))
mask[crow,ccol]= 0.000001
# 求D0
d0 = mask[rows-1,cols-1]*0.5
# 用公式计算值并赋值给掩膜,阶次这里设置为1,可以根据需要来设或者求出来。
for i in range(rows):
for j in range(cols):
mask[i,j] = 1 / (1 + np.power(d0.astype(float) / mask[i,j].astype(float), 2 * 1))
# 由于傅里叶变换使图像变为双通道(x+yi),所以掩膜也是要双通道的。
mask = cv2.merge((mask, mask))
# 用掩膜对图像进行处理
src_dft_shift_over=src_dft_shift*mask
#将中心移回左上角
src_dft_shift_over_ishift=np.fft.ifftshift(src_dft_shift_over)
# 傅立叶逆变换
src_dft_shift_over_ishift_idft=cv2.idft(src_dft_shift_over_ishift)
#后续操作,将矢量转换成标量,并映射到合理范围之内
src_dft_shift_over_ishift_idft=cv2.magnitude(src_dft_shift_over_ishift_idft[:,:,0],src_dft_shift_over_ishift_idft[:,:,1])
src_dft_shift_over_ishift_idft=np.abs(src_dft_shift_over_ishift_idft)
src_dft_shift_over_ishift_idft=(src_dft_shift_over_ishift_idft-np.amin(src_dft_shift_over_ishift_idft))/(np.amax(src_dft_shift_over_ishift_idft)-np.amin(src_dft_shift_over_ishift_idft))
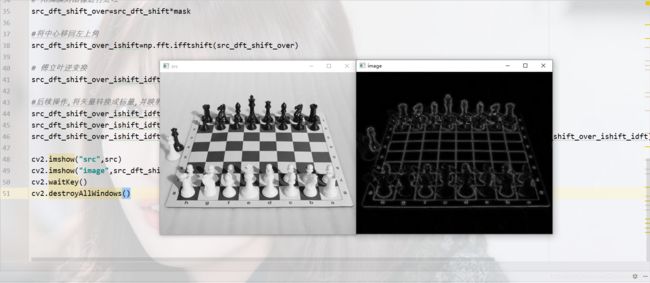
cv2.imshow("src",src)
cv2.imshow("image",src_dft_shift_over_ishift_idft)
cv2.waitKey()
cv2.destroyAllWindows()