机器学习实战笔记9——深度神经网络

任务安排

1、机器学习导论       7、逻辑回归
2、KNN及其实现       8、核方法
3、K-means聚类       9、深度神经网络
4、主成分分析          10、？
5、线性判别分析       11、？
6、贝叶斯方法

      加上这次课只剩下三节课，开始进入到深度学习的范畴了，虽然已经学了不少机器学习相关的知识了，但感觉还是远远不够，期待开学后的实训和以后的课程能更深入地学习人工智能！

深度神经网络（DNN）

      20世纪80年代以来，人们大量借用神经生理学的概念来研究人工智能，诞生了一门新兴学科——人工神经网络（artificial neural networks，ANN），简称神经网络（neural netwroks，NN）
      人工神经网络的基本思想：根据对自然神经系统构造和机理的认识，神经系统是由大量的神经细胞（神经元）构成的复杂的网络，人们对这一网络建立一定的数学模型（如MLP） 和 算法（如BP），设法使它能够实现诸如基于数据的模式识别、函数映射等带有“智能”的功能
      在神经网络的数学模型中，最有影响的模型是多层感知器（multi-layer perceptron，MLP），实际上，多层感知器就是深度神经网络（deep neural networks，DNN）的模型，多层感知器属于上次提到的 非线性分类器

Ⅰ 神经元与感知器

      （讲到神经网络，需要科普一点生物知识作为基础）
      一个神经元（neuron）就是一个神经细胞，是神经系统的基本组成单位。

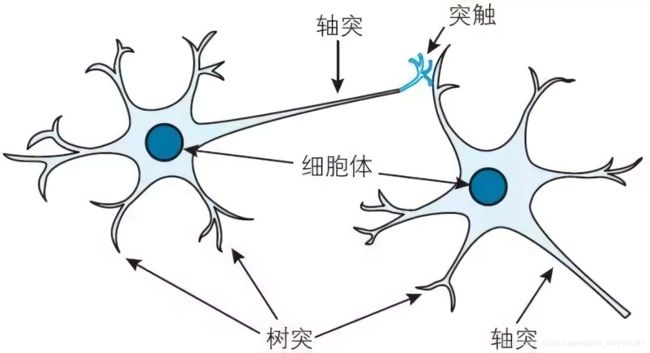
      如图，一个典型的神经元由这些部分组成：
      （1）细胞体（cell body），神经细胞的主体，内有细胞核和细胞质，除了实现细胞生存的各种基本功能外，还是神经细胞进行信息加工的主要场所；
      （2）树突（dendrites），细胞体外围的大量微小分支，是细胞的“触角”，一个神经网络的树突可达 $10^3$ 数量级，多数长度很短，主要担负着从外界（其他细胞或体液环境）接受信息的功能；
      （3）轴突（axon），细胞的输出装置，负责把信号传递给另外的神经细胞，通常每个神经元由一个轴突，有的轴突很长，如人体四肢的某些神经细胞的轴突长达 $1m$ 以上
      (4)突触（synapse），一个神经元的轴突与另一个神经元的树突相“连接”的部位，这种连接并不是物理上的直接接触，而是二者细胞膜的充分靠近，通过之间的微小缝隙传递带电离子
      神经系统中的信号是电化学信号，靠带电离子在细胞膜内外的浓度差来形成和维持的，这种信号以脉冲的形式沿着轴突传播，经突触把电荷传递给下一个神经元。突触的不同状态影响信号传递的效率，称之为突触的连接强度。神经元之间通过突触连接，构成复杂的神经网络。

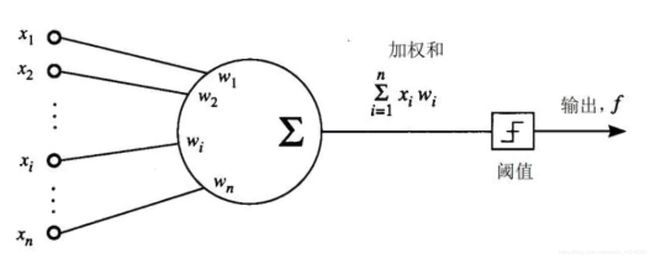
      一个典型的神经元简化工作过程：外界电信号通过突触传递给神经元，当细胞收到的信号总和超过一定阈值后，细胞被激活，通过轴突向下一个细胞发送电信号，完成对外界信息的加工
      如上图 （阈值逻辑单元（threshold logic unit,TLU）：McCulloch-Pitts神经元模型） 所示，$x_1,...,x_n$ 表示神经元的多个树突接收到的信号，$n$ 是向量 $x$ 的维数，$w_1,...,w_n$ 称作权值，反映各个输入信号的作用强度。神经元将这些信号加权求和，当求和超过一定阈值后神经元即进入激活状态，输出值 $y=1$；否则神经元处于抑制状态，输出值 $y=0$;
      用公式表示该模型：$$y=\theta (\sum _{i=1}^n{w}_i{x}_i+{\omega }_0)$$      其中 $\theta ()$ 是单位阶跃函数（也可以是符号函数 $sgn()$），称为神经元的传递函数（激活函数）
      几何意义上来理解，一个感知器神经元就是一个线性分类器，用超平面$$\sum _{i=1}^n{w}_i{x}_i+{\omega }_0=0$$      把特征空间分为两个区域，$y=1$ 及 $y=0(-1)$
      套用 Rosenblatt 的感知器准则函数及利用梯度下降法迭代求解，得到权值的迭代训练修正函数：$$w(t+1)=w(t)+\eta (t)[d(x(t))-y(t)]x(t)$$      $d(x)$ 代表训练样本 $x$ 的正确分类，$t$ 为迭代次数记数，$x(t)$ 是当前时刻考查的样本，$\eta (t)$ 是训练步长，当两类数据线性可分时，上述神经元权值迭代算法能够在有限步内收敛到一个使所有训练样本都正确的解

★ Ⅱ 前馈网络（FNN）

      对于单个感知器，只能解决线性分类问题（如与AND、或OR、非NOT问题），无法解决非线性分类问题（异或XOR），理论上来说，是可以像之前线性分类器的组合实现非线性分类器那样，通过感知器的组合来实现多层学习模型，来解决非线性分类问题——多层感知器诞生了
      通常把多个神经元相互连接组成的系统称作人工神经网络，而把由多个感知器组成的神经网络称作多层感知器网络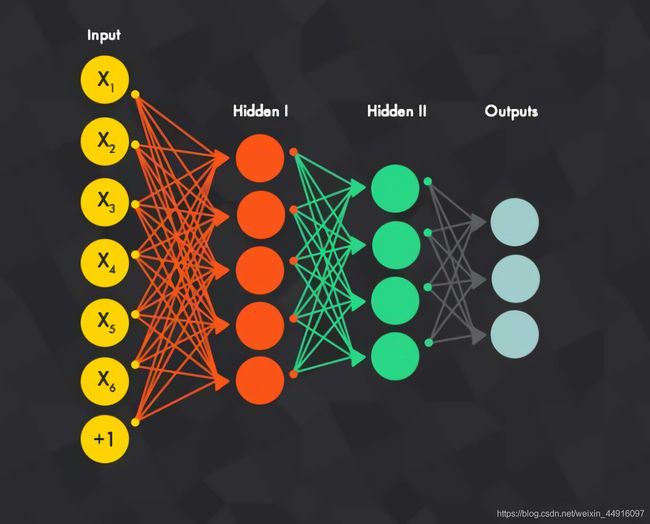
      如图，多层感知器实现的是从 $d$ 维输入 $x$ 到输出 $y$（一维或多维）的一个映射。它由多个采用 $Sigmoid$ 传递函数（激活函数）的神经元节点连接而成，这些神经元节点分层排列，每一层的神经元接受来自前一层的信号，经过加工后又传递给后一层
      多层感知器的第一层是输入层$（input$ $layer）$，每个节点对应于 $x$ 的每一维，节点本身并不完成任何处理，只是把每一维的信号“分发”到后一层的每个节点。最后一层是输出层$（out$ $layer）$，如果 $y$ 是一维，则输出层只有一个节点。输入层和输出层各层都被称作“隐层”$（hidden$ $layer）$，其中的节点称作“隐节点”$（hidden$ $nodes）$，因为它们全都“隐藏”在输入层和输出层之内，隐层神经元的个数即为网络模型的宽度，层的个数即为网络模型的深度，故多层感知器也被称为深度神经网络
      类似这种形式的神经网络即被称作前馈神经网络（feedforward neural networks，FNN），是神经网络的主要结构形式之一。在前馈神经网络中，信号沿着输入层到输出层方向单向流动，输入层把信号传给隐层，隐层再把信号传递给下一个隐层，最后一个隐层把信号传递给输出层。这种神经网络实现了从输入层到输出层的映射。把一个样本特征向量的各分量分别输入到网络输入层的各个对应节点上，经过网络上从前向后一系列加工运算，在输出端得到相应输出向量。
      对于网络层次的叫法，通常有两种：①输入输出各一层，隐层 $n$ 层，如图则是四层网络；②输入层不计入，则如图是三层网络
      对于一个实现从 $x$ 到 $y$ 的映射的三层感知器，可以用函数表示为$$y=g(x)=f(\sum _{j=1}^{n_H}{w}_{ij}f(\sum _{i=1}^d{w}_{ij}{x}_i))$$      其中 $f()$ 是 $Sigmoid$ （或其他激活函数），$d$ 是输入 $x$ 的维数（输入层节点个数），$w_{ij}$ 是从输入层第 $i$ 个节点到隐层第 $j$ 个节点的权值（连接强度），$wjk$ 是从隐层第 $j$ 个节点到输出层第 $k$ 个节点的权值
      常见的激活函数通常有：$Sigmoid$ 函数、$tanh$ 函数、$Relu$ 函数、 PReLU 函数（性能通常更优）、$ELU$ 函数、$MaxOut$函数等，实际使用时一般根据模块提供的都试一遍过去看哪个效果好…
      前馈网络的目标是逼近于某个函数，通过学习让映射函数逼近于分类函数，得到某些参数最优解，只是它其中一个方面的应用而已，研究发现，任何一个从 $x$ 到 $y$ 的非线性映射，都存在一个适当结构的三层前馈神经网络能够以任意精度逼近它

★ Ⅲ 反向传播算法（BP）

      对于上述提到的前馈神经网络，会有一个疑问，为什么激活是 $Sigmoid$ 函数，而不是之前常用来分类的阶跃函数 $\theta$ 或符号函数 $sgn$ 呢？
      根据前面提到的感知器学习算法，核心思想是梯度下降法，即以训练样本被错分的程度为目标函数，训练中每次出现错误时便使权系数朝着目标函数相对于权系数的负梯度方向更新（使其下降），直到目标函数取得极小值即没有训练样本被错分。
      实验表明，这种感知器学习算法无法直接应用到多层感知器上，因为激活函数作为阶跃函数（对于权值的反馈只有0、1之分），得到输出端的误差只能对最后一个感知器的权值进行训练，无法对前面感知器的权值进行调整，起初的解决办法是提前给定其他感知器的权值，但最终模型的性能很大程度上取决于能否设计出恰当的权值，给模型优化造成了非常大的阻碍，甚至对于感知器的研究因此停滞了25年之久！？直到后来 反向传播算法（back propagation，BP） 的提出，人工神经网络迎来飞速发展。
      而算法突破的关键主要是将阶跃函数 $\theta$ 替代为了 $Sigmoid$ 函数，$Sigmoid$ 函数在 逻辑回归 有介绍过，不赘述了，其特点是单调递增的非线性函数，无限次可微，权值较大时逼近阶跃函数，权值小时逼近线性函数，用 $Sigmoid$ 函数作为激活函数，则数学表达式可以写成$$y=f(x)=\frac{1}{1+e^{-{\sum }_{i=1}^n{w}_i{x}_i-w_0}}$$      至此，前馈网络（通常以 $Sigmoid$ 函数作为激活函数），不管网络结构多么复杂，总可以通过计算梯度来考查各个参数对网络输出的影响，通过梯度下降法调整各个参数
$$神经网络\{\begin{array}{l}神经网络结构\\ 神经元激活函数\\ 权值\end{array}$$
      实际应用中，网络结构和激活函数都是事先定好的，而权值是根据 BP 算法求得的，以下算法步骤分析以前馈网络结构及 Sigmoid 激活函数为基础
      核心思想： 训练开始前，随机赋予各权值一定的初值。训练过程中，轮流对网络施加各个训练样本。当某个训练样本作用于神经网络输入后，利用当前权值计算神经网络输出（这是一个信号从输入到隐层再到输出的过程，称为前向过程）。考查所得到的输出与训练样本的已知正确输出之间的误差，根据误差对这些节点权值的偏导数修正这些权值，以此类推，直到把各层权值都修正一次。然后，从训练集中抽出另外一个样本进行相同的训练过程。不断重复，一轮训练终止直到总误差水平达到预先设置的阈值，或者训练时间达到预设上限。
输入：样本集 { $x_i,y_i$}${}_{i=1}^n$，步长 $\eta$，小批量大小 $mini-batches$，迭代次数 $T$
输出：训练后收敛的神经网络
      1.确定神经网络结构，用小随机数进行权值初始化，设训练时间 $t=0$
      2.从训练集中得到一个训练样本 $x=[x_1,x_2,...,x_n{]}^T\in R^n$，记它的期望输出为 $D=[d_1,d_2,...,d_m{]}^T\in R^m$，样本通常随机地从训练集中抽取
      3.计算在 $x$ 输入下当前神经网络的实际输出$$y=f(\sum _{s=2}^{n_{L-2}}{w}_{sr}^{l=L-1}\dots f(\sum _{j=1}^{n_1}{w}_{jk}^{l=2}f(\sum _{i=1}^n{w}_{ij}^{l=1}{x}_i)))$$
      4.从输出层开始调整权值,第l层修正公式:$$w_{ij}^l(t+1)=w_{ij}^l(t)+△w_{ij}^l(t)$$      上标 $l$ 表示从第 $(l-1)$ 层到 $l$ 层的权值，$△w_{ij}^l=\eta {\delta }_j^l{x}_i^{l-1}$ 为权值修正项，对于输出层 ${\delta }_j^l=y_j(1-y_j)(d_j-y_j)$，是当前输出与期望输出之间的差值对权值的导数；对于隐层 ${\delta }_j^l=x_j^l(1-x_j^l){\sum }_{k=1}^{n_{l+1}}{\delta }_k^{l+1}{w}_k^{l+1}$，是输出误差反向传播到该层的误差对权值的导数
      5.在更新全部权值后对所有训练样本重新计算输出，计算更新后的网络输出与期望输出的误差。 检查算法终止条件，如果达到则停止，否则 $t$ $+=1$，返回第二步。算法终止条件通常设定为该轮训练中网络实际输出与期望输出之间的平均平方误差小于某一阈值，或该轮训练中所有权值变化都小于某一阈值，或训练次数达到上限

      手写验算

Ⅳ 泛化能力

      泛化能力，即机器学习算法对新鲜样本的适应能力
      神经网络由于具有大量的参数，很强的非线性变换能力，因而也很容易导致在训练集上过拟合，训练集上准确率很高，损失很低，但在测试数据上效果很差，也就是缺乏泛化能力，不能适应新样本

过拟合产生的原因：
      1）数据集有噪声
      2）训练数据不足
      3）训练模型过度导致模型非常复杂

解决方法：
      1）降低模型复杂度（缩小宽度和减小深度）
      2）数据集扩增（平移，旋转，缩放，剪切，添加噪音）
      3）正则化。
      4）加入droupout，让神经元以一定的概率不工作。
      5）early stopping
      6）ensemble（集成学习），特征融合。

Ⅴ 架构设计

通常有三种做法（均带有试探性）来选择多层感知器网络的隐层节点数目和隐层个数
      ①根据具体问题进行试探选择。 选择几个不同的隐层节点数目，分别对训练样本集进行试验，采用留一法或其他方法交叉验证，根据交叉验证的错误率来选择较好的节点数目。也有一些基本经验，如通常隐层节点数目应该小于输入维数，训练样本数较小时应该适当采用少的隐层节点（如输入节点数一半左右）
      ②根据对问题的先验知识精心设计隐层节点数和层数，如有人设计了多层神经网络进行手写体数字识别，有些隐层专门为考虑数字的旋转不变形和某些变形不变性
      ③用算法确定隐层节点数，如**裁剪法：**初始时采用较多的隐层节点，在采用 BP 算法进行权值学习时增加一条额外目标，要求所有权值的绝对值或平方和尽可能小，这样，一部分多余的隐节点的权值会逐渐变小。在学习到一定阶段时，检查各个隐节点权值，将过小的隐节点删除，剩余神经网络重新学习

今日任务

任务解决

1、对于 Digits 手写字，直接用 sklearn 里的模型就能得到非常好的分类效果了（如果要跑 MINST 数据集，就模仿后面 CIFAR-10 一样在 PyTorch 里自己构建神经网络模型）

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from myModule import clustering_performance


def sklearn_MLP(*data):
    X_train, X_test, y_train, y_test = data
    mlp = MLPClassifier(solver='adam', hidden_layer_sizes=[100, 100], activation='relu',
                        random_state=62, max_iter=2000, learning_rate_init=0.0001)
    mlp.fit(X_train, y_train)
    y_predict_mlp = mlp.predict(X_test)
    print('MLP分类器')
    print('Testing Score: %.4f' % clustering_performance.clusteringMetrics1(y_test, y_predict_mlp))
    # print(mlp.loss_)
    # return clustering_performance.clusteringMetrics1(y_test, y_predict_mlp)


# Digits手写字
digits = load_digits()
X_train_digits, X_test_digits, y_train_digits, y_test_digits = \
    train_test_split(digits.data, digits.target, test_size=0.2, random_state=22)
print('Digits')
sklearn_MLP(X_train_digits, X_test_digits, y_train_digits, y_test_digits)

★ 2、对于 CIFAR-10，需要利用 pytorch 自己构建神经网络模型，代码偏多、偏复杂
数据读取之前在 逻辑回归 里面有提过
深度学习步骤：
                   ①构建网络结构
                   ②加载数据集
                   ③训练神经网络（优化器、损失函数）
                   ④测试神经网络

深度学习有几个重要概念需区分一下：

名词	定义
Epoch	使用训练集的全部数据对模型进行一次完整训练，称为 “一代训练”
Batch	使用训练集中的一小部分样本对模型权值进行一次反向传播的参数更新，该一小部分样本被称为 “一批数据”
Iteration	使用一个 Batch 数据对一次模型进行一次参数更新的过程，称为 “一次训练”

$$Batch-number=\frac{Train-data-size}{Batch-size}$$

例：
      CIFAR-10 数据集有 60000 张图片作为训练数据，10000 张图片作为测试数据。假设现在选择 Batch_Size = 100 对模型进行训练，迭代 30000 次
● 每个 Epoch 训练图片数量：60000（全部）
●     每个 Epoch 需完成 Batch 个数
    = 每个 Epoch 具有 Iteration 个数
    = 每个Epoch 中模型发生权重更新次数
    = Batch_number = 60000 / 100 = 600
● 总共迭代 30000 次 = 30000 / 600 = 50 个 Epoch

梯度下降方式区别

梯度下降方式	Train-data-size	Batch-size	Batch-number
BGD	N	N	1
SGD	N	1	N
Mini-Batch	N	B	$\frac{N}{B}$(除不尽时+1)

$$
代码

import torch
import torch.nn.functional as F  # 激励函数的库
from torchvision import datasets
import torchvision.transforms as transforms

path = 'C:/Users/1233/Desktop/Machine Learning/CIFAR10/'
# 定义全局变量
n_epochs = 10  # epoch 的数目
batch_size = 20  # 决定每次读取多少图片

# 定义训练集个测试集
train_data = datasets.CIFAR10(root=path, train=True, transform=transforms.ToTensor())
test_data = datasets.CIFAR10(root=path, train=True, transform=transforms.ToTensor())

# 创建加载器
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, num_workers=0)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size, num_workers=0)
# num_workers可以＞0,是调用系统子进程来跑,但是Windows可能会因为各种权限问题报错


# 建立一个四层感知机网络
class MLP(torch.nn.Module):  # 继承 torch 的 Module
    def __init__(self):
        super(MLP, self).__init__()
        # 初始化三层神经网络 两个全连接的隐藏层，一个输出层
        self.fc1 = torch.nn.Linear(3072, 512)  # 第一个隐含层
        self.fc2 = torch.nn.Linear(512, 128)  # 第二个隐含层
        self.fc3 = torch.nn.Linear(128, 10)  # 输出层

    def forward(self, din):
        # 前向传播， 输入值：din, 返回值 dout
        din = din.view(din.size(0), 3072)  # .view( )是一个tensor的方法,使得tensor改变size但是元素的总数是不变的
        # din = din.view(-1, 28 * 28)  # 将一个多行的Tensor,拼接成一行
        dout = F.relu(self.fc1(din))  # 隐层激活函数 relu
        dout = F.relu(self.fc2(dout))
        dout = F.softmax(self.fc3(dout), dim=1)  # 输出层激活函数 softmax
        # 10个数字实际上是10个类别,输出是概率分布,最后选取概率最大的作为预测值输出
        return dout


# 训练神经网络
def train():
    # 定义损失函数和优化器
    lossfunc = torch.nn.CrossEntropyLoss()  # 交叉熵损失函数
    # SGD随机梯度下降法,lr学习率(步长),这里随机梯度和小批量随机梯度共用.SGD
    optimizer = torch.optim.SGD(params=model.parameters(), lr=0.01)
    # 开始训练
    for epoch in range(n_epochs):
        train_loss = 0.0
        for data, target in train_loader:
            optimizer.zero_grad()  # 清空上一步的残余更新参数值
            output = model(data)  # 得到预测值
            loss = lossfunc(output, target)  # 计算两者的误差
            loss.backward()  # 误差反向传播, 计算参数更新值
            optimizer.step()  # 将参数更新值施加到 net 的 parameters 上
            train_loss += loss.item() * data.size(0)
        train_loss = train_loss / len(train_loader.dataset)
        print('Epoch:  {}  \tTraining Loss: {:.6f}'.format(epoch + 1, train_loss))
        # 每训练一epoch,测试一下性能
        test()


# 在数据集上测试神经网络
def test():
    correct = 0
    total = 0
    with torch.no_grad():  # 训练集中不需要反向传播
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, 1)  # 前面一个返回值数据不是我们想要的
            total += labels.size(0)
            correct += (predicted == labels).sum().item()

    print('Accuracy of the network on the test images: %d %%' % (100 * correct / total))
    return 100.0 * correct / total


# 实例化感知器网络
model = MLP()

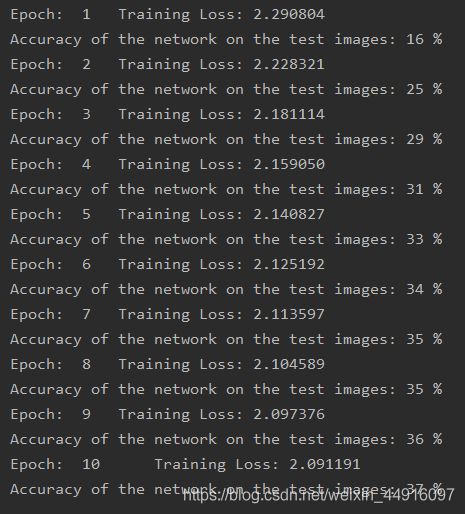
train()

效果图
可以明显看见随着每一次epoch的参数更新以后，网络性能在逐渐变好，但性能优化速率在下降，最终性能应该还是可以修改一些超参数提高的

参考：深度学习之BP算法
           使用 PyTorch 实现 MLP 并在 MNIST 数据集上验证
           Pytorch中文文档
           训练神经网络中最基本的三个概念：Epoch, Batch, Iteration