基于深度学习的云反演-文献分析

---

前言

本科生的卫星遥感课的结课考核中想要吃透一篇论文，并做到很好的展示是不容易的，尤其是还牵涉了深度学习的网络。这里仅分享我们小组在完成整个任务过程中的相关资料整理，给其他面临同样任务的同学提供思路。

一、基础概念

1.深度学习：

深度学习是学习样本数据的内在规律和表示层次，这些学习过程中获得的信息对诸如文字，图像和声音等数据的解释有很大的帮助。它的最终目标是让机器能够像人一样具有分析学习能力，能够识别文字、图像和声音等数据。 深度学习是一个复杂的机器学习算法，在语音和图像识别方面取得的效果，远远超过先前相关技术。
典型的深度学习模型有卷积神经网络( convolutional neural network)、DBN（深度信任网络模型）和堆栈自编码网络(stacked auto-encoder network)模型。

2.反演：

定量遥感是指在基于模型知识的基础上，依据可测参数值去反推目标的状态参数。或者说，根据观测信息和前向物理模型，求解或推算描述地面实况的应用参数（或目标参数）。现阶段，定量遥感发展的一个主要障碍是反演理论的研究不足。

3.云反演：

云在地球系统能量平衡和水循环中扮演着至关重要的作用，其特征的准确获取对于理解大气物理过程、改进天气和气候模拟具有重要意义。云遥感反演是了解云特征、评估卫星云观测能力的。就宏观特征来说，可以分为三个类别:云识别或云量的探测方法、云边界的确定方法以及云相态的反演方法。就微观特征来说，(地基)云遥感反演方法基本分为两大类型，最优化求解法和经验参数化方法。
云在地球系统辐射能量平衡和大气水循环中扮演着至关重要的作用。对于辐射能量平衡，云通过反射太阳辐射使得地面白天不会太热，通过阻挡长波辐射使得夜间不会太冷从而使得地球适合人类生存。在大气水循环方面，江河湖海的水汽蒸发以后通过云和降水为陆地提供重要的淡水资源。云对辐射的调节能力和形成降水的多少与云的宏微观特征紧密相关。然而，云特征的观测一直存在较大误差，云的表征也是模式天气预测和气候预估中最大的不确定性因子。

4.云观测方式：

云宏微观特征可以通过原位观测和遥感观测获得，包括飞机原位观测、地基和卫星遥感观测。飞机观测在各类观测中的准确度最高，但由于观测成本高和观测环境不能过于恶劣等原因而造成观测时间、观测次数和观测样本有限。飞机观测数据通常用于云发展过程和特征的个例研究和参数化构建而很难用于获取长时间或大范围的云宏微观特征。卫星遥感观测包括静止卫星和极轨卫星观测，分别具有较高的时间分辨率和空间分辨率，且能够实现大范围观测，因此在云特征观测上具有很大的独特优势，被广泛用于云特征的反演、统计研究和模式模拟评估研究。然而，卫星云观测的不确定性相对较大，时间和空间分辨率相对于飞机和地面还是过于粗糙而无法用于很多云相关过程研究。地面云遥感观测精度多介于飞机和卫星观测之间、时间分辨率高且能长时间连续观测，并且可以与地面多种仪器观测配合，共同反演云特征或彼此进行印证。
在实际应用中，飞机原位观测多用于对地面或卫星遥感观测的诊断和评估；地面遥感观测多用于对卫星遥感观测和模式模拟研究的诊断和评估，而卫星遥感观测多用于对模式模拟研究的诊断和评估。

5.不同反演方法的差异：

在宏观特征方面，由于主动遥感仪器垂直分辨率的差异，云回波信号的临界值选取等问题，各个方法在云识别、云边界和云相态的反演上还存在着较大差异。在微观特征方面，由于很多云遥感反演方法采纳的数据不同、方法理论基础存在差异、所使用的假设不同、以及根据不同飞机观测采纳的经验参数也不同，不同云反演产品间存在着较大差异，为准确或可靠的使用这些云产品造成困扰。

6.云宏观特征与观测仪器：

云的宏观特征包括云量、云出现频率、云顶高度、云底高度、云顶温度、云底温度、云几何厚度和云光学厚度等；目前云宏观特征观测的仪器主要包括云高仪 (Ceilometer)、云雷达 (Millemeter cloud radar，MMCR)、微脉冲激光雷达 (Micropulse lidar，MPL)、探空廓线 (Radiosonde)、拉曼激光雷达等。

7.云微观特征：

云微观特征包括云相态、云水含量、云粒子谱分布、云滴数浓度、冰晶形状、冰水含量、云滴有效半径等。

8.云的遥感观测流程：

云的遥感观测首先是确定云的存在与否，即云识别问题，同时可以基于观测进一步判定云量或者云的频率。当判定有云以后，第二步是获取云的宏观特征，即云底高度、云顶高度、云底温度、云顶温度、云厚等特征。第三步一般是对云相态的确定，区分水云、冰云以及混合云。针对不同的云相态，分别采取不同的遥感反演方法进一步获取云的微观特征，也就是第四步。即第五步，基于获取的云宏微观特征，结合对云的理论认知，获取其它未直接反演获得的云宏微观物理量，如云水含量、云滴数浓度等。

二、研究问题概述

1.研究内容：

根据冰云太赫兹辐射特性实现的一种预分类的神经网络算法，能够从太赫兹亮温中分别反演得到冰、霰（xian,四声）两种粒子的统计参数和廓线分布。（冰云的冰相粒子除了固态的冰粒子（Ice）外， 还存在有空气、液态水和固态冰混合构成的霰粒子(Graupel)）

2.新意点：

目前的太赫兹冰云反演算法将不同种类冰相粒子（主要是冰和霰）视为冰粒子统一计算。该算法能进一步区分冰相粒子，突破现有研究仅仅计算单一冰粒子的局限，更加符合冰云真实情况。

3.研究过程概述：

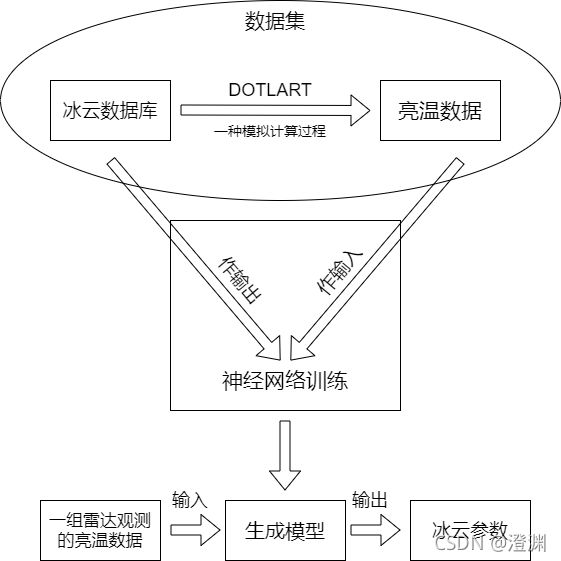
首先基于WRF（模式预报场）数值模式和 ATMS（微波载荷实际探测）载荷真实观测的冰云霰数据构建了包含冰、霰粒子密度廓线的混合冰云数据库，然后使用 DOTLRT （辐射传输模式）模拟 183GHz-874GHz七个频段的星载太赫兹冰云探测亮温，最后开展冰云参数探测仿真试验，验证反演算法性能。

4.反演结果：

得到冰、霰两种粒子的路径总量、等效粒径、等效云高和密度廓线。

5.研究原因：

目前全球大气模式之间的冰云分布存在显著差异，全球和区域平均云冰量相差一个数量级，造成这种模式间差异的主要原因是当前还缺乏足够的全球冰云探测数据。获取全球冰云参数（高度、冰水路径、等效粒径）的真实观测对于改善大气数值模式中的对冰云的表征性能，减少气候预测和气象预报的不确定性。

6.使用太赫兹的原因：

微波辐射计探测仪只对 500 μm 以上的大尺寸冰晶敏感，而红外和可见光频段的探测仪只对 50 μm 以下的小尺寸冰晶敏感。而处于以上两者之间的太赫兹频段，其波长范围与冰云粒子尺寸分布接近，探测范围能够覆盖冰云的全部冰晶尺寸，兼顾了穿透能力与敏感性，因此星载太赫兹辐射探测仪对于冰云探测具有独特的优势。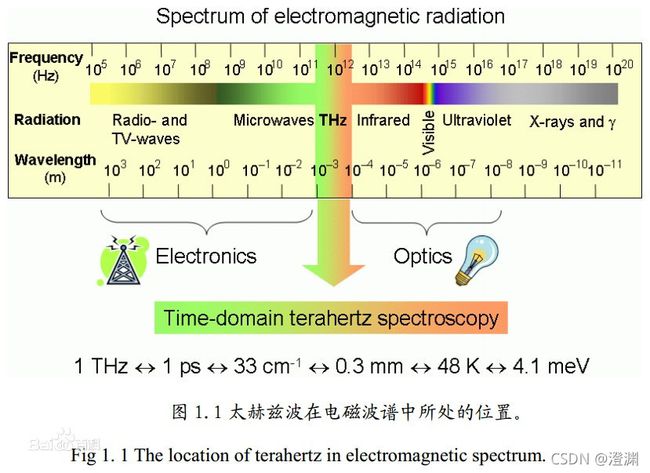

三、原理

1模拟：

辐射传输模式通过对微分辐射传输方程求解实现从大气物理参数到大气辐射亮温的映射计算。（为何利用公式构建？目前全球还没有在轨运行的太赫兹频段大气探测载荷，因此本文使用大气辐射传输模式计算模拟的太赫兹冰云探测亮温数据）NOAA的两位科学家Voronovich 和 Gasiewski(2004)使用离散纵标法对差分辐射传输方程求解而实现的离散正切线性辐射传输模式。DOTLRT 输入参数除了常规的表面辐射率、气压、高度、大气温度和水汽廓线外，还支持五种水凝物，包括云液态水、雨、冰、雪、霰，仿真频率可高至 1000 GHz，适用于本论文的太赫兹频段仿真。本文研究的太赫兹冰云探测频率通道采用了和ICI （欧空局计划发射的一颗卫星上的星载太赫兹冰云成像仪）相同的频率再外加更高 874.38 GHz（后面会提到这些同为太赫兹波段的检测差异） 频率以提升对小尺寸粒子探测的灵敏度。

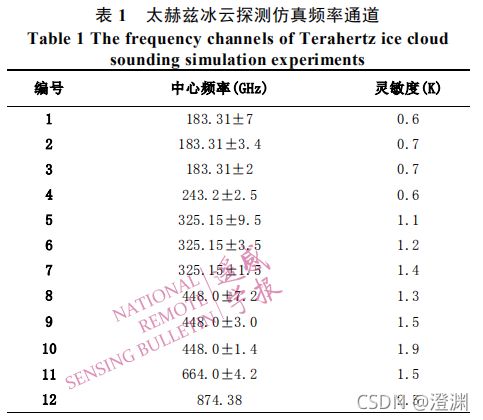
（体现选用的频率通道的图，一则是和欧空局卫星一致，二则是多了一个非常敏感的874.38通道）

2.数据库：

试验案例选择了 2016 年经过我国南海的台风“尼伯特”和台风“莫拉蒂”。大气和冰云参数以美国 NCEP(National Centers for Environmental Prediction) 的 GFS(Global Forecast System for Medium Range)再分析资料作为边界场和初始场，使用 WRF（模式预报场） 数值预报模式 6 小时预报输出。1）WRF模式预报的台风对流区域的冰云霰密度廓线 GWC与真实数值差异较大，而从对比验证结果来看，ATMS（美国NPOESS卫星上微波大气探测载荷的名字） 探测的 NDE L2 的 GWC 数据相比 WRF 模式预报的 GWC 数据更加准确；2）在 183GHz（霰粒子也仅仅考察这个频段） 频段冰云的霰粒子对亮温的影响是最明显的；3）DOTLRT模拟亮温可以较好的反映台风对流区域的冰云特征。因此本文采用 WRF 数据+NDE L2 霰数据混合构建大气冰云数据库。

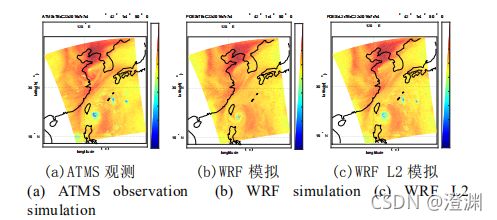
（仅考察两个频段的比较放在这里，明显看出模式预报场的直接模拟情况与观测值差别较大，而模式预报场与L2级数据产品的混合模拟更加准确）
PS：GWC霰密度廓线
GWP霰密度路径
IWC冰密度廓线
IWP冰密度路径

（L2级数据只提供GWP不提供IWP，所以这里对于廓线的考察是只有GWP，当然，可以观察到与前面所述同样的规律，即L2级数据包含的信息更全面，可以看出霰粒子不仅分布在台风中心区域，在外围螺旋云带区域也存在，与 ATMS 观测亮温图像中的低温冰云区域分布更加一致）
将来真正利用这些数据在冰云探测卫星的反演上时还需要考虑卫星的时空匹配问题。

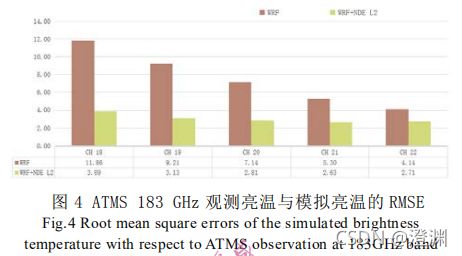
（以183GHZ附近的频率段为例，直接用均方根差来衡量误差大小时也可以明显看出WRF与L2级数据混用的优势，在183 GHz 最远翼频率通道 183.31±7 GHz（最左边两个条形图），RMSE 从WRF 模拟亮温的 11.9 K 下降到 3.9 K，下降幅度最大，在最中心的 183.31±1 GHz 频率误差也从 4.1 K下降到了 2.7 K（最右边两个条形图））

3.冰云参数：

全球差异大，高达一个数量级，是大气数值模式不确定性的最大来源。冰云参数差异产生的原因主要是由于不同的数值模式对冰粒子特性和将云冰转化为降水的阈值做出了不同的假设。XWC是冰云含量廓线 ，XWP 是冰云总路径，是 XWC 在高度上的积分（X就表示可以是冰I也可以是霰G）。Dme 是有效粒子尺寸，是粒子的质量加权中位尺寸，也为粒子等效直径。Zme 等效云高定义为 XWP 一半时对应的高度。（这都是一些重要的参数）

（表达XWP与XWC关系的式子）

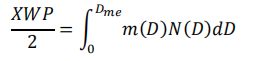
（可以解释Dｍｅ的公式，是权重乘以一个粒子尺寸分布函数在０～Dｍｅ上积分等于冰云总路径的一半）

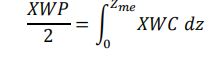
（Zme 等效云高定义为 XWP 一半时对应的高度）

4.总结：

从 183GHz-874 GHz 亮温图像来看，DOTLRT 计算的亮温图像能够反映台风对流区域的冰云粒子散射造成的低温值，与 ATMS 真实观测的冰云区域一致（DOTLRT计算结果与实际一致说明合理），而且在太赫兹频段最高的 664 GHz和 874 GHz，低温区域明显扩大（最后两张图上蓝区明显扩大），说明在太赫兹高频更小的冰云粒子散射效应变强，能够对大气上视辐射亮温造成下降，这与辐射传输理论也是吻合的（应该是指频率越高辐射能量越大）。

四、算法及数据分析

将冰云分为冰、霰两种粒子构成时，太赫兹频段的冰云亮温下降是由两种粒子共同散射作用引起的，由于冰、霰两种粒子尺寸分布、介电常数不同，具有不同的散射谱特性，因此在使用神经网络反演冰云参数时需要将两种粒子分开。

1.霰粒子：

神经网络算法的训练数据库需要两部分数据，一是亮温数据作为输入，由 DOTLRT 模拟亮温实现，二是冰云数据作为输出，由输入到 DOTLRT 模式的冰云数据库实现。将两部分数据组成数据对，选择以台风“莫拉蒂”的亮温-冰云数据对作为训练数据集，台风“尼伯特”的数据对作为测试数据集（生成好的模型需要测试一下看看是否有可以接受的准确度）。本文用神经网络算法分别实现冰云霰粒子的统计参数和垂直密度廓线 GWC 的反演（不管是对冰粒子还是霰粒子都是这样两大块内容），反演的霰参数包括路径总量 GWP、等效粒径 G_Dme、等效云高 G_Zme三个参数。

（1）反演流程：

霰的统计参数反演试验流程如下：①对数据库中的亮温数据进行筛选，筛选依据是霰粒子散射在 183.31+7 GHz 频率引起的亮温差超过该频率通道灵敏度 0.6 K 时，则认为对应的霰粒子总量 GWP 能够被准确探测到，从 DOTLRT 亮温中计算得到对应 GWP 门限阈值为 12 g/m2。②使用作为训练集的台风“莫拉蒂”数据训练神经网络，网络隐藏层采用 32 个神经元（见最后），训练函数为 trainscg（归一化共轭梯度法,是唯一一种不需要线性搜索的共轭梯度法），网络收敛判别指标采用 mse（均方误差）。③将训练好的网络（即上自制流程图中所说的生成好的模型）对测试数据集中的台风“尼伯特”模拟观测亮温进行反演，得到霰参数。④将反演得到的霰参数估值与测试数据集中对应的真实霰参数进行对比分析，评估反演精度。

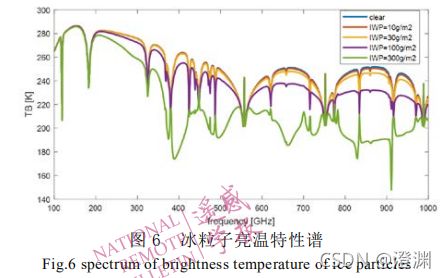
（对霰粒子主要是研究１８３ＧＨｚ的原因，可以从图中看出在１８３GＨｚ附近不论IWP怎么变，也就是不论冰路径怎么变，灵敏度都是很高的，换句话说此时对灵敏度产生贡献的主要是霰粒子，也即可以使用神经网络算法从 183 GHz 频段亮温先单独反演冰云的霰粒子参数。）

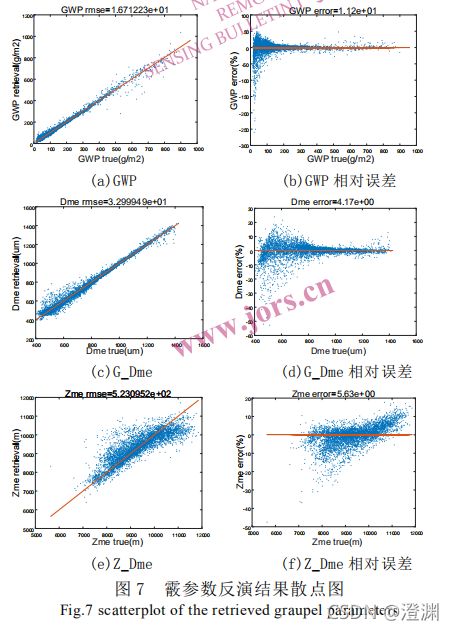
（使用了 4500 个样本训练，3000 个样本测试，关于每个图的特点需要特别分析，见本文“六”）

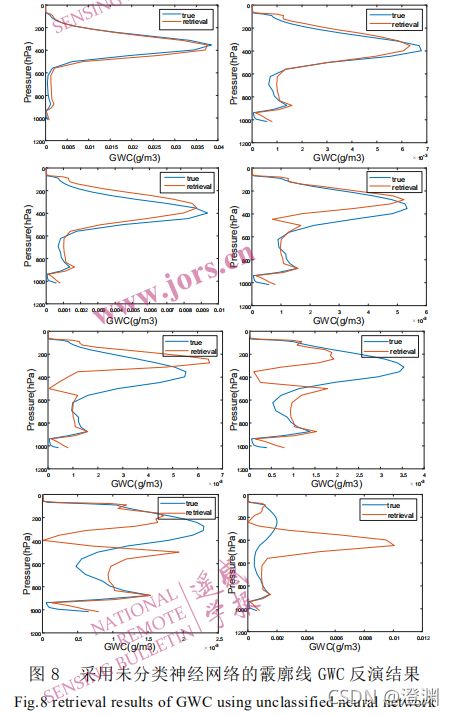
（数据不经预处理直接去训练模型会因为数据复杂度高，表征性差，而导致训练出来的模型效果差，真值和反演结果不一致）

（2）GWC（同流程，研究从参数变成了廓线）：

误差很大，表征性差。我们研究发现，GWP 对具有不同形状的霰廓线样本具有较好的指示关系（意味着可借助GWP来推GWC，知道一个GWP可以推出一个GWC），可以将 GWP 值作为霰廓线样本分类的指示器。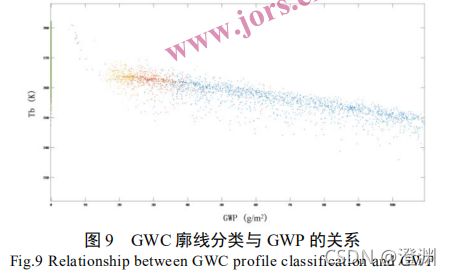

（指示关系：颜色代表的是几种廓线，每一个廓线样本点都会在横轴上对应一个具体的GWP，可以明显看出蓝色类廓线样本最多，蓝色代表低层与高层峰值比< 1/3，橙色为峰值比在 1/3-2/3 之间；黄色为峰值比在 2/3-5/3 之间；紫色为峰值比在 5/3-5之间，这些都是廓线的特征，图上大致是只有蓝色黄色橙色三色样本，因此把廓线分为因此可以将所有霰廓线按照 GWP 值划分为三类，对应的 GWP 取值区间分别为 GWP > 35 g/m2，25 <= GWP < 35 g/m2， 和 15 <= GWP < 25 g/m2）
（在深度神经网络的训练中，样本差异过大很难划分为一类，比如无毛猫和长毛猫虽然都是猫，但在分类时不可能划为一类，廓线在此也是，只有对廓线进行进一步细分，才能保证每一类都具有较强的表征性，才能训练出一个从全局看都合理的模型，当然这些不同类型的廓线同样可以再统一一个标签叫廓线来方便人为读取）

（3）预分类：

加入数据预分类的霰廓线神经网络反演试验流程如下：①对训练数据集中的冰云廓线样本根据GWP 三种阈值（蓝色，橙色，黄色）进行分类；②使用三种类型的训练样本分别训练三个神经网络；③对测试数据集中的所有亮温数据使用 3.2 节中的神经网络反演得到 GWP（测试数据集提供的也是廓线，肯定是要统一成GWP才能比较）；④将测试数据集的亮温数据样本根据上面的 GWP三种阈值进行分类；⑤对分类的亮温数据样本使用对应的网络反演得到霰廓线 GWC（其实这里反演结果第一步也还是GWP，是由GWP推GWC，看看用模型的GWP效果同原始真值效果如何）。可以看出分类后的二、三类样本误差值远小于未分类的误差，验证了预分类对提升这些样本反演精度的有效性。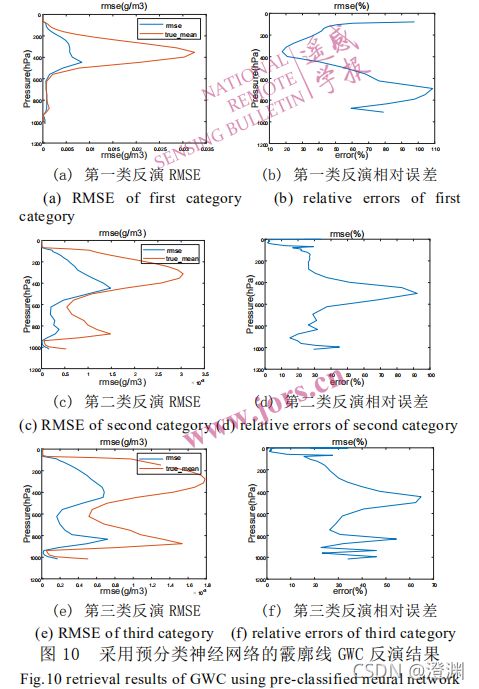

（ 10 (a) © (e)中红线是反演GWC 的均值，蓝线是 RMSE，即均方根差。(b) (d) (f)是 RMSE与 GWC 真值比值，代表相对误差。）
（所谓三类样本是说对廓线化成了三类，所谓全部样本又是说，用上了参与实验的所有台风的样本）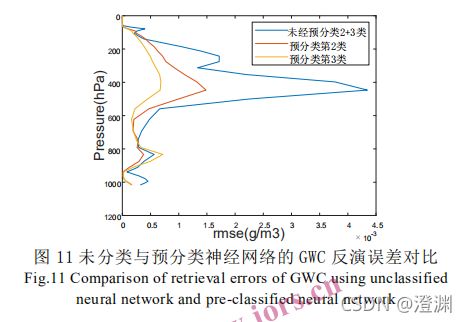

（只拎出二三类霰廓线分析考虑也可看出分类后效果好转明显，误差明显小了）
间接反演法（用廓线还可以再反演回参数）两种方式反演的冰云霰参数精度基本相当。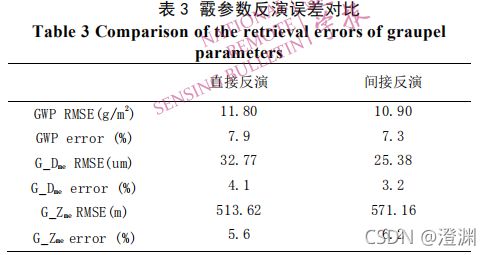

（霰廓线还可以反推霰参数，但看出误差也是有的参数升高有的参数降低，只能说间接反演法和直接反演霰参数大差不差）

2.冰粒子：

在 183 GHz 频段，亮温的冰云散射可以认为仅仅来自于霰粒子的贡献，但在更高的太赫兹频段，散射由冰和霰粒子共同引起。因此要从太赫兹亮温中反演冰粒子参数，需要将之前反演的霰密度廓线作为先验约束条件，再使用神经网络算法根据冰粒子引起的散射亮温差反演得到冰粒参数。具体实现方法是首先从 WRF 预报大气参数中去除冰参数，再加上反演的霰密度廓线 GWC 输入 DOTLRT 模式得到不包含冰粒散射的模拟亮温，然后将无冰亮温和观测亮温相减，则此亮温差代表了冰粒对大气辐射亮温的贡献。
对冰粒子的反演仍然分为统计参数和垂直密度廓线 IWC 的反演，反演的冰参数也是路径总量 IWP、等效粒径 I_Dme、等效云高 I_Zme。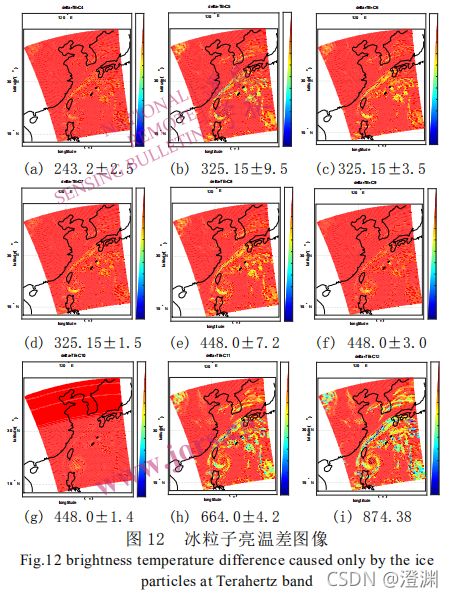

（跟前面那张有１２张图的相比，就是少了１８３GHZ系列的三张，用剩下这些频段进行研究）

（1）参数反演流程：

与霰类似，冰参数的筛选条件是当样本IWP 引起的亮温差值超过 874.38 GHz 频率的系统噪声 2.5 K 时，则认为对应的冰云样本可以准确探测到，计算得到对应 IWP 门限阈值为 5.5 g/m2。对比实验（比较不同频段组合反演的参数精度）说明更多的太赫兹探测频段能够明显提升冰粒子参数反演精度。

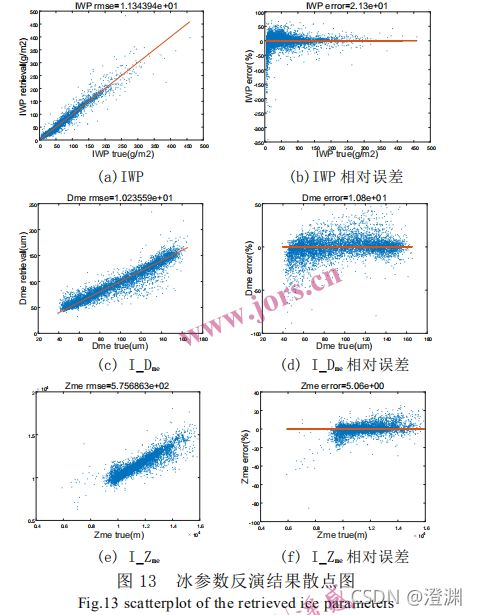
（６０００个训练样本，６０００个测试样本，研究的频段多了，相应样本也更充裕一些）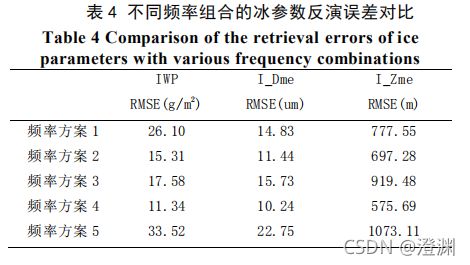

（既然研究的频段不再单一，那混合起来研究可能会比对某一个频段研究效果要好，事实证明，频率方案４利用起来243
GHz +325 GHz +448 GHz +664 GHz +874 GHz 5 个频段的９个频率通道这种情况下误差最小）

（2）IWC（也是从参数到廓线）：

冰粒子主要分布在 7-15 km 高度范围内，且不同冰云样本的高度分布差异较大。因此冰密度廓线 IWC 反演问题与 GWC 类似，同样具有较高的复杂性，使用神经网络算法反演IWC 同样需要进行数据预分类。I_Zme < 10 km 为一类，I_Zme 在 10-15 km 范围内的，按照 1 km 等高度间距分类（一共６类）。

（3）预分类（类比霰粒子）：

加入数据预分类的冰廓线神经网络反演试验流程如下：①对训练数据集中的冰云廓线样本根据上述 I_Zme 的六种阈值进行分类；②使用六种类型的训练样本分别训练六个神经网络；③对测试数据集中的所有亮温差数据使用类霰粒子的神经网络算法反演得到 I_Zme；④将测试数据集中的亮温差数据样本根据 I_Zme 的六种阈值进行分类（必须统一成I＿Ｚｍｅ才能比，把测试集也化成Ｉ＿Ｚｍｅ）；⑤对分类的亮温差测试数据使用对应的网络反演得到冰廓线（再检验精度）。

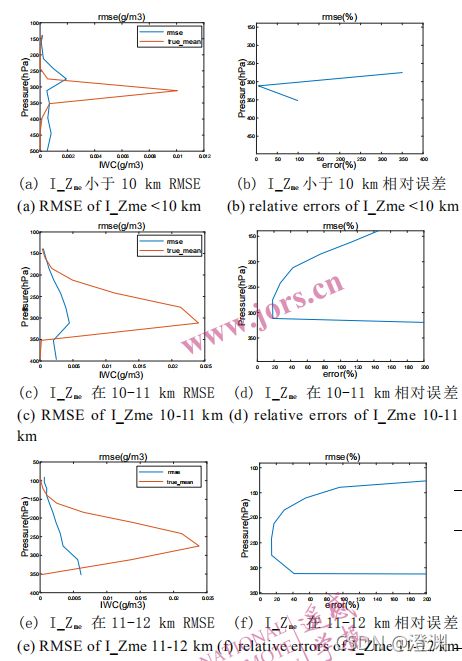
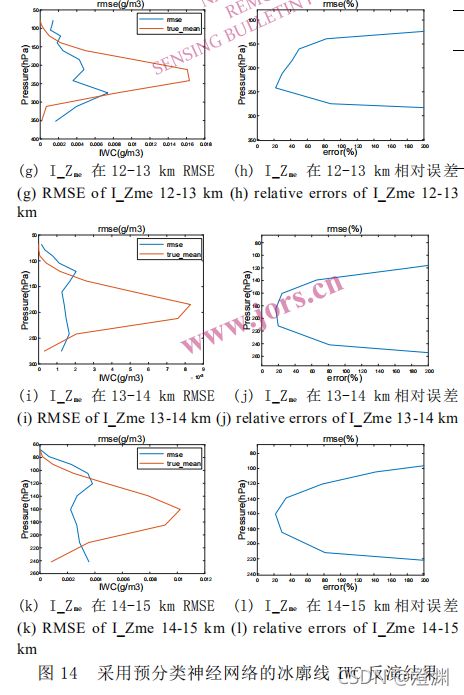
（详细见“六”）

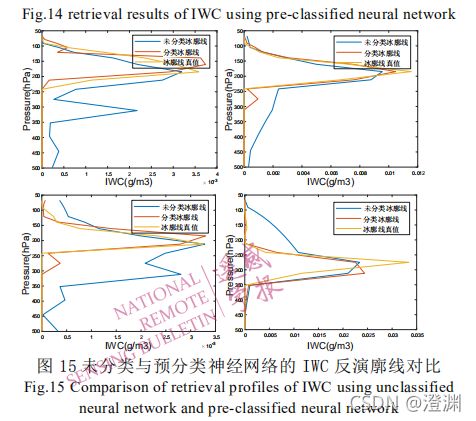
（拎出几类看还是预分类效果会好一些）
常规神经网络反演的冰廓线 IWC 可能会在本没有冰分布的高度上引入较大的误差，而预分类神经网络反演的冰廓线 IWC 更加符合实际分布。但是无论对哪种高度的冰云进行反演时，云顶与云底的反演误差都较大。这是因为虽然按照云高对冰云廓线样本进行了预分类，但冰云厚度的差异依旧会对反演结果造成影响。

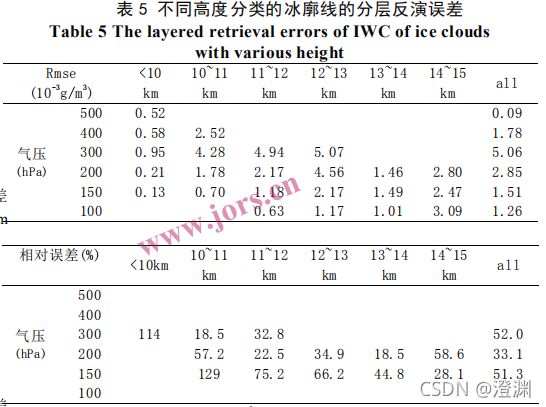
（详细见“六”）
I_Dme 和 I_Zme 采用间接反演方法的反演精度更高，IWP 采用神经网络直接反演算法精度更高。但是这一结论还需要更多样本测试来支持。

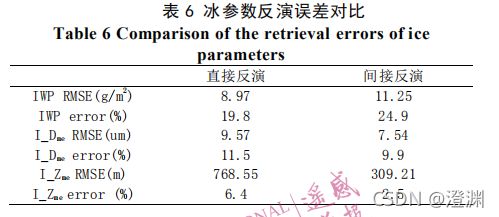
（冰廓线还可以反推冰参数，但看出误差也是有的参数升高有的参数降低，只能说间接反演法和直接反演霰参数大差不差）（事后老师又强调准确说明差多少可能汇报效果更佳）

五、深度学习细讲

1.神经网络诞生：

在开始介绍前，有一些知识可以先记在心里：

1.设计一个神经网络时，输入层与输出层的节点数往往是固定的，中间层则可以自由指定；
2.神经网络结构图中的拓扑与箭头代表着预测过程时数据的流向，跟训练时的数据流有一定的区别；
3.结构图里的关键不是圆圈（代表“神经元”），而是连接线（代表“神经元”之间的连接）。每个连接线对应一个不同的权重（其值称为权值），这是需要训练得到的。
神经元（单元\节点）：神经元模型是一个包含输入，输出与计算功能的模型。输入可以类比为神经元的树突，而输出可以类比为神经元的轴突，计算则可以类比为细胞核。下图是一个典型的神经元模型：包含有3个输入，1个输出，以及2个计算功能。中间的箭头线。这些线称为“连接”。每个上有一个“权值”，而权值并非一开始就给出的，而是通过训练得到的。这些连接是最重要的东西，一个神经网络的训练算法就是让权重的值调整到最佳，以使得整个网络的预测效果最好。（每个有向箭头表示的是值的加权传递）

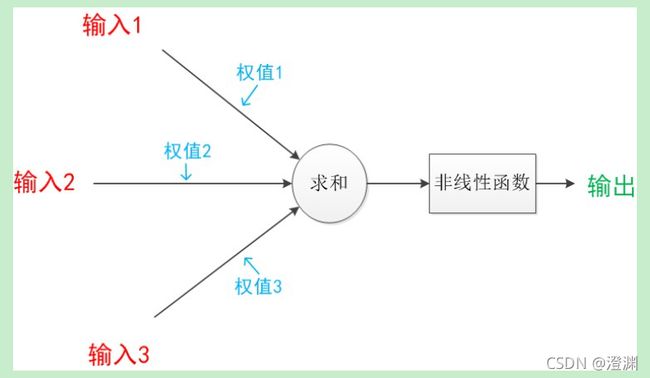
（可以类比生物概念的神经元，非常像一个神经细胞，虽然这里只有一个输出，但事实上也可以有多个输出，因为前期过程一样这里的多个输出也是一样的，只不过要去连接的下一个神经元会有所不同）
神经元可以看作一个计算与存储单元。计算是神经元对其的输入进行计算功能。存储是神经元会暂存计算结果，并传递到下一层。

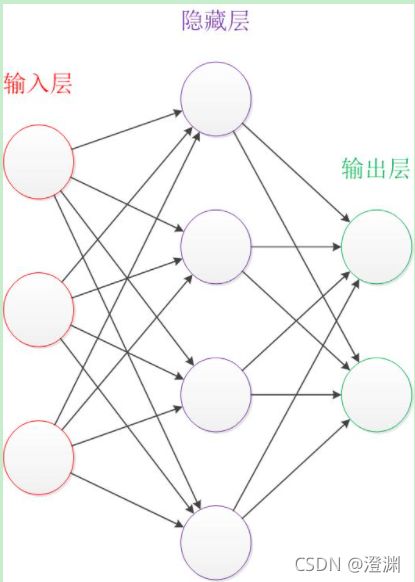
2.隐藏层：

其意义就是把输入数据的特征，抽象到另一个维度空间，来展现其更抽象化的特征，这些特征能更好的进行线性划分。因为从隐藏层到输出层也会是生成一个线性分界线，所以隐藏层是对原始的数据进行了一个空间变换，使其可以被线性分类，然后输出层的决策分界划出了一个线性分类分界线，对其进行分类，关键在于隐藏层和输入层之间的联系。而隐藏层节点的个数是取决于设计者的，这其中没有一定之规，多靠经验判定，然后比较各个选取节点数的训练效果，文中采用的是32个神经元训练的模型，效果已经相对比较准确。

3.机器学习究竟如何实现：

1.前面提到了权重，首先给所有权重参数赋上随机值。我们使用这些随机生成的参数值，来预测训练数据中的样本。样本的预测目标为yp，真实目标为y。那么，定义一个值loss，计算公式如下。loss = (yp - y)2这个值称之为损失（loss），我们的目标就是使对所有训练数据的损失和尽可能的小。我们可以进一步把损失写为关于权重参数（parameter）的函数，这个函数称之为损失函数（loss function）。下面的问题就是求：如何优化参数，能够让损失函数的值最小。（优化到极致之后，得到的权重便是最终生成模型里的权重了，从而模型也就得到了。）
2.一般来说解决这个优化问题使用的是梯度下降算法。梯度下降算法每次计算参数在当前的梯度，然后让参数向着梯度的反方向前进一段距离，不断重复，直到梯度接近零时截止。一般这个时候，所有的参数恰好达到使损失函数达到一个最低值的状态。(就当求导来理解，极值点对应着的最优点)
3.可能还需要使用反向传播算法（从后往前算每一层与前一层的梯度值）。反向传播算法是利用了神经网络的结构进行的计算。不一次计算所有参数的梯度，而是从后往前。首先计算输出层的梯度，然后是第二个参数矩阵的梯度，接着是中间层的梯度，再然后是第一个参数矩阵的梯度，最后是输入层的梯度。计算结束以后，所要的两个参数矩阵的梯度就都有了。
4.如果说前三步都是在为优化服务的，那机器学习不只有优化，因为它不仅要求数据在训练集上求得一个较小的误差，在测试集上也要表现好。因为模型最终是要部署到没有见过训练数据的真实场景。提升模型在测试集上的预测效果的主题叫做泛化（generalization），相关方法被称作正则化（regularization）。神经网络中常用的泛化技术有权重衰减等。
事实上，前面所述也仅是两层的神经网络的训练方式，真正的深度学习是更多层的，比如最早关于多层的“深度信念网络”有一个“预训练”（pre-training）的过程，这可以方便的让神经网络中的权值找到一个接近最优解的值，之后再使用“微调”(fine-tuning)技术来对整个网络进行优化训练。
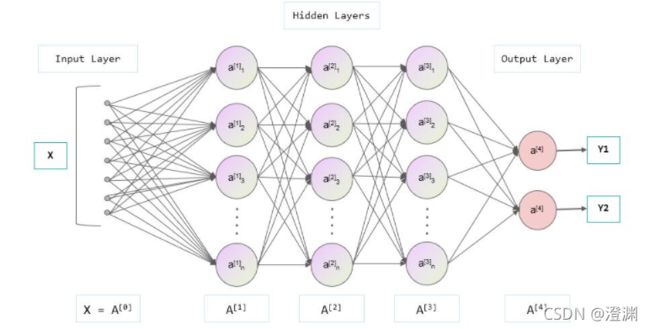
多层神经网络中，输出也是按照一层一层的方式来计算。从最外面的层开始，算出所有单元的值以后，再继续计算更深一层。只有当前层所有单元的值都计算完毕以后，才会算下一层。有点像计算向前不断推进的感觉。所以这个过程叫做“正向传播”。改变中间层的神经元数目，会引入更多的参数，更多的参数意味着其模拟的函数可以更加的复杂，可以有更多的容量（capcity）去拟合真正的关系，可以提升网络的表示能力；而在参数相同的情况下，改变每一个中间层的神经元数目，可以调整加深整个网络的深度，通过研究发现，在参数数量一样的情况下，更深的网络往往具有比浅层的网络更好的识别效率。
多层意味着更深入的表示特征，以及更强的函数模拟能力。更深入的表示特征可以这样理解，随着网络的层数增加，每一层对于前一层次的抽象表示更深入。在神经网络中，每一层神经元学习到的是前一层神经元值的更抽象的表示。例如第一个隐藏层学习到的是“边缘”的特征，第二个隐藏层学习到的是由“边缘”组成的“形状”的特征，第三个隐藏层学习到的是由“形状”组成的“图案”的特征，最后的隐藏层学习到的是由“图案”组成的“目标”的特征。通过抽取更抽象的特征来对事物进行区分，从而获得更好的区分与分类能力。
多层神经网络中，训练的主题仍然是优化和泛化。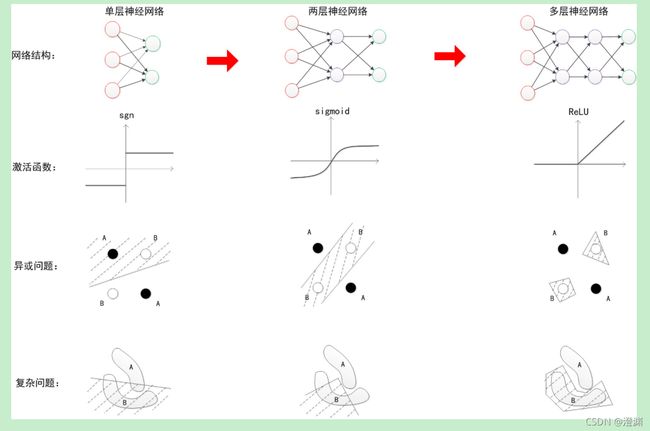

4.Relu函数：

目前在深度学习中，最流行的非线性函数是ReLU函数。ReLU函数不是传统的非线性函数，而是分段线性函数。其表达式非常简单，就是y=max(x,0)。简而言之，在x大于0，输出就是输入，而在x小于0时，输出就保持为0。这种函数的设计启发来自于生物神经元对于激励的线性响应，以及当低于某个阈值后就不再响应的模拟。

六、霰、冰参数即廓线反演结果分析（应该是不在讲稿但是可能要讲的出来的内容）

是在上文中出现的表。

1.霰参数反演结果分析：

7(a)是反演的 GWP散点图，总体上大部分数据点都分布在 x = y 的对角线附近，说明反演 GWP 值与真值比较接近，均方根误差 RMSE 为 16.7 g/m2。从数据分布来看，绝大部分冰云样本点位于 GWP < 500 g/m2 的范围，而在GWP >500 g/m2 的范围里绝对误差变得更大，出现更多明显偏离对角线的散点。
而从图 7(b)展示的GWP 相对误差散点图来看，反而是 GWP 越小相对误差越大，总体来说 95%以上测试数据的 GWP 反演相对误差能够控制在±50%以内，只有 GWP < 100 g/m2 的部分样本相对误差超过这个范围。
图 7©是反演的 G_Dme 散点图，总体上大部分数据点都分布在 x = y 的对角线附近，说明反演 G_Dme 值与真值比较接近，均方根误差 RMSE 为 33.0 μm。从数据分布来看，绝大部分冰云样本点位于 G_Dme < 1400 μm 的范围，而在 G_Dme < 800 μm 的范围里绝对误差变得更大，出现更多明显偏离对角线的散点。
而从图 7(d)展示的 G_Dme 相对误差散点图来看，反而是 G_Dme 越小相对误差越大，大部分测试数据的G_Dme 反演相对误差能够控制在±20%以内。
图 7(e)是反演的 Z_Dme 散点图，总体上都分布在 x = y 的对角线两侧，均方根误差 RMSE 为 523.1 m。从数据分布来看，绝大部分冰云样本点位于 7 km < Z_Dme < 12 km 的范围，而在 8 km < Z_Dme < 9 km 和 Z_Dme > 10 km 的范围里绝对误差变得更大，出现更多明显偏离对角线的散点。
而从图 7(f)展示的 Z_Dme 相对误差散点图来看，大部分测试数据的 Z_Dme 反演相对误差能够控制在±2０％以内。

2.霰廓线反演结果分析：

从反演的绝对误差来看，第一类样本误差值最大，RMSE 范围为[0,8.2×10-3] g/m3，第二类样本RMSE 范围为[0,1.5×10-3] g/m3，第三类样本误差值最小，RMSE 范围为[0,0.7×10-3] g/m3。这主要是由于三类样本是按照 GWP 大小——即冰云厚度来划分的。（意思是绝对误差会因为本身数值不同而有差异）
但从相对误差来看，三类样本就整体趋于一致，误差绝大部分都在 60%以下。横向对比三类样本的相对误差，可以发现，850-550 hPa 范围对应霰廓线第二峰值，第一类样本误差最大，是因为第一类样本的峰值集中在 550 hPa 以上，第二峰值处霰密度值较小导致相对误差大；450-350 hPa 对应廓线第一峰值，第一类样本误差最小，反演精度最高。由于第一类样本数占比达到了 82%，可以看到全部样本的平均误差与第一类样本误差最为接近，预分类主要改进了冰云较薄的二三类样本的反演精度。

3.冰参数反演结果分析：

总体上三种参数的大部分数据点都分布在 x=y 的对角线附近，说明反演的冰参数值总体上精度较好。IWP 的 RMSE 为 11.34 g/m2， 在 IWP > 120 g/m2 时，绝对误差变得更大，出现更多明显偏离对角线的散点。从相对误差来看，除具有非常小 IWP 值的样本点相对误差较大外，总体相对误差都能控制在±50%以内。I_Dme 的 RMSE 为 10.24 μm，I_Dme 在 100-140 μm 时绝对误差更大，相对误差基本集中在±30%以内。I_Zme 的 RMSE 为575.69 m，在 I_Zme 低于 10 km 和高于 14 km 时绝对误差更大，相对误差基本集中在±20%以内。

4.冰廓线反演结果分析：

左边的(a) © (e) (g) (i) (k)中红线是 6 种不同高度样本反演冰廓线的均值，蓝线是均方根误差 RMSE，右边的(b) (d) (f) (h) (j) (l)是反演 RMSE 与廓线真值相比的相对百分比误差。表 5 列出了 6 种不同高度廓线在不同气压层的反演误差平均值和相对误差。从反演 IWC 的各层RMSE 值和相对误差分布来看，基本上也是在 IWC值越大的高度，反演绝对误差越大，但是相对误差越小，大部分冰云样本在冰云密集高度的相对误差都能控制在 50%左右，说明对 IWC的反演精度较好；但每种分类的云顶和云底位置相对误差显得偏大，说明由于云层厚度的不同，边界上的特征不明显，冰云厚度的差异依旧会对反演结果造成影响。
由表５从不同高度的冰云反演误差图像来看，小于 10 km 分类采用了 159 个样本训练，13 个样本测试，所选范围数据较少，RMSE 范围为[0，0.0019] g/m3，仅在 IWC 廓线峰值高度的反演误差< 100%，此分类样本数据较少，但分布高度存在较大差异，因此反演误差较大；10-11 km 分类采用了 1337 个样本训练，392 个样本测试，反演 RMSE范围为[0，0.0045] g/m3，在冰云密集的高度范围350-200 hPa，相对误差在 50%以内，在峰值对应高度约 310hPa，相对误差仅有 18.9%；11-12 km 反演RMSE范围为[0，0.0061] g/m3，在冰云密集范围 320-160hPa，相对误差在 50%以内，在 IWC 廓线峰值对应高度约 270hPa，相对误差仅为 15%左右；12-13 km分类使用了 813 个样本训练，365 个样本测试，反演 RMSE 范围为[0,0.0074] g/m3，在廓线分布的主要高度 250~160hPa 相对误差小于 50%， IWC 廓线峰值对应高度约 240hPa，相对误差大小最小，为 21.7%；13~14km 分类使用了 458 个样本训练，258 个样本测试，反演 RMSE 范围为[0，0.0021]g/m3，在 IWC廓线主要范围 230-150hPa，相对误差在 50%以内，在廓线峰值约 180hPa 处，相对误差最小，约为 17%；14~15km 使用了 235 个样本训练，133 个样本测试，反演 RMSE 范围为[0,0.0038]g/m3，在 IWC 廓线主 要范围 190~130hPa，相对误差在 50%以内，在廓线峰值约 160hPa 处，相对误差最小，约为 22%。从不同云高的反演结果可以看出，神经网络每一类型廓线主要分布高度范围相对误差都在 50%以内，峰值对应高度约为 20%。

总结

本文参考的文献是《基于神经网络的太赫兹冰云探测反演算法研究》一文与《地基云遥感反演及挑战》博客园的《神经网络浅讲：从神经元到深度学习》这里附上连接link.
最后的一点建议是我们在这次文献阅读中的收获，虽然都是从完全不懂的阶段去入手但还是要先弄明白自己研究的大方向里每一个小的基础概念，才能去理解论文中别人所讲的算法，更能理解它的目的。