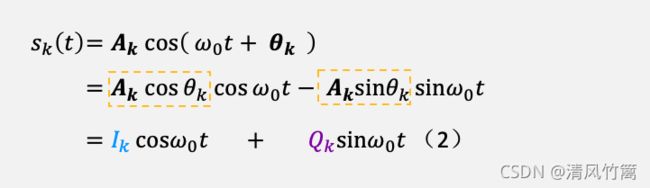16QAM调制的仿真及其Python实现的代码（超级详细）

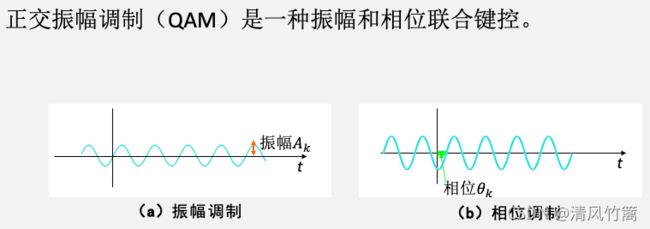
       要进行QAM调制的仿真首先要了解QAM调制的基本原理。QAM调制是一种根据数字基带信号同时控制载波的幅度和相位的调制方式。也就是说对应不同的1和0的基带信号，载波的幅度和相位都可以发生变化。

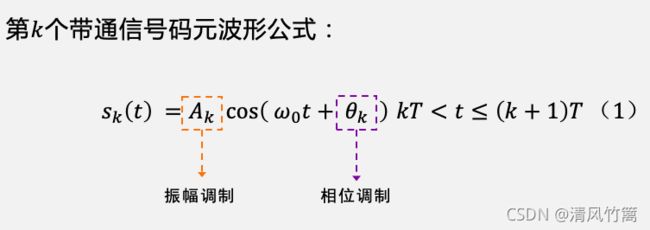
 根据这个调制方式可以得到QAM的带通信号的公式可以表示为

 根据这个公式我们还不能进行仿真。我们还需要将这个公式做进一步的展开。

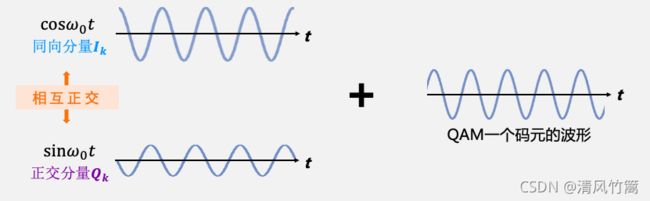
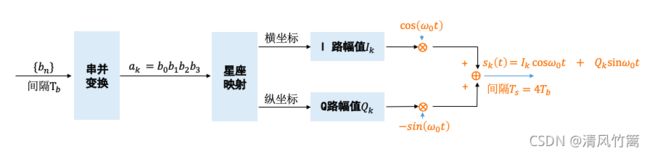
查看展开后的公式可以发现，一个QAM信号的码元波形，可以通过I路和Q路两路幅度调制的信号叠加而成。由于cost和sint是正交的，所以这是两路正交信号的叠加。

 

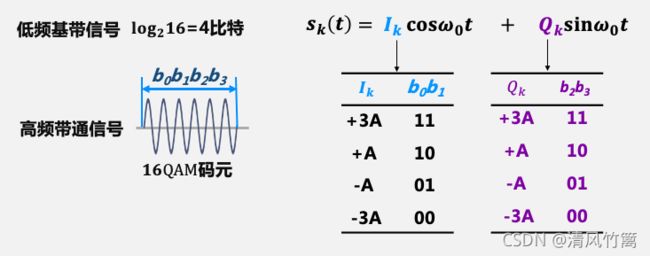
所以，如果我们想要的到一个QAM信号的码元波形，就要分别得到I路的幅度值，和Q路的幅度值。这里以16QAM为例进行说明。由于16QAM是16进制的，每4个比特为一组对应一个带通信号的码元波形。 对于给定的基带信号的比特流，就要每4个为一组，每一组绘制出对应的带通信号的码元波形。

 基带信号的4个比特，有16种不同的比特组合。

 要进行仿真就要给出这16种比特组合中，每种比特组合对应的带通信号的码元波形是多少。要想得到码元波形，就要知道I路和Q路的幅度值分别是多少。

接下来 就设定仿真中1和0的比特组合对应的I路和Q路的幅度值如下。将I路振幅对应前两个比特b0b1，Q路对应后两个比特b2b3。I路信号的四个振幅+3A +A -A -3A与比特b0b1的四个组合11 10 01 00相对应。Q路信号也采用相同的对应关系。

 这样对于一个基带信号的比特组合，我们就可以对应到I路和Q路的不同幅度值。

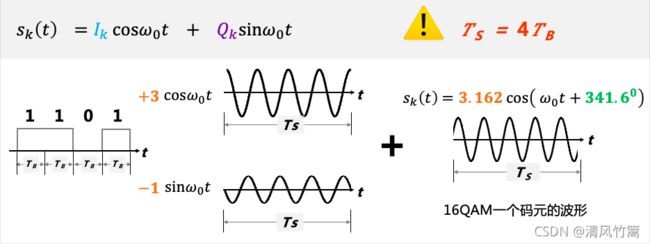
例如基带信号中的1101。前面的两个比特11就对应I路幅度值+3A，后面两个比特01对应着Q路幅度值-A。这样基带信号1101对应的两路正交载波的振幅就可以得到了。

 将I路载波乘以3进行振幅调制，Q路载波乘以-1进行振幅调制.再将两路正交载波经过振幅调制后的波形想加就得到了16QAM调制后的波形。可以发现1101对应的码元波形振幅为3.162A，相位为341.60 。需要注意的是16QAM带通信号码元宽度应该是基带信号码元宽度的4倍。

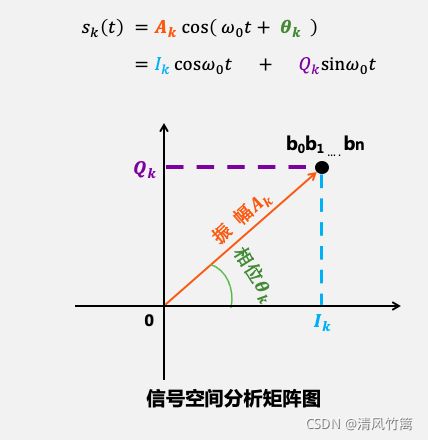
由于在仿真中每个码元信号的波形，要对应一个I路幅度值，一个Q路幅度值，还有码元本身的幅度值和相位。

 

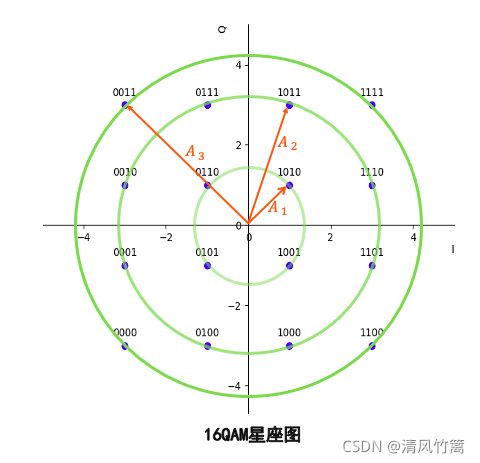
这种复杂的对应关系可以保存在一个星座图中。

 矩阵图中的一个点对应了一种比特组合，到原点的距离对应着带通信号的振幅，该点的相位对应这带通信号的相位。该点的横坐标对应I路振幅，纵坐标对应Q路振幅。这样就将比特组合对应带通信号直观的展现出来了。16QAM有16中比特组合，因此星座图中就有16个点。

 接下来我们看一下如何进行16QAM星座和波形的Python仿真。

首先是星座图的绘制。

import  numpy as np
import matplotlib.pyplot as plt


digram = {'11':3,'10':1,'01':-1,'00':-3}#设置数字和幅度的对应关系
spots = {}#放置点

plt.figure()
plt.xlabel('I',loc='right',labelpad = 0.5)
plt.ylabel('Q',loc='top',labelpad = 0.5)  # 设置坐标轴的文字标签

ax = plt.gca()  # get current axis 获得坐标轴对象

ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')  # 将右边 上边的两条边颜色设置为空 其实就相当于抹掉这两条边

ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')  # 指定下边的边作为 x 轴 指定左边的边为 y 轴

ax.spines['bottom'].set_position(('data', 0))  # 指定 data 设置的bottom(也就是指定的x轴)绑定到y轴的0这个点上
ax.spines['left'].set_position(('data', 0))


plt.axis([-5,5,-5,5])#设置坐标的数字范围

for i in ['0','1']:
    for j in ['0','1']:
        for k in ['0','1']:
            for p in ['0','1']:
                 str = ''.join([i,j,k,p])#通过循环获得16个4位数的10组合
                 str1 = ''.join([i,j])#前两个10组合
                 a = digram[str1]#获取前两个10组合对应的幅值
                 # a = int(a)

                 str2 = ''.join([k,p])
                 b = digram[str2]#获取后两个10组合对应的幅值
                 # b = int(b)

                 complexSpot = complex(a,b)#不能写为a+bj，因为编译不通过 生成坐标
                 plt.scatter(a,b,c='black')#绘制点
                 plt.text(a, b+0.3, str, fontsize=10, color = "black", weight = "light", verticalalignment='center', horizontalalignment='center', rotation=0)#绘制10组合
                 tempspot = {str:complexSpot}#获得数字组合和点
                 spots.update(tempspot)#存入点的集合

plt.show()

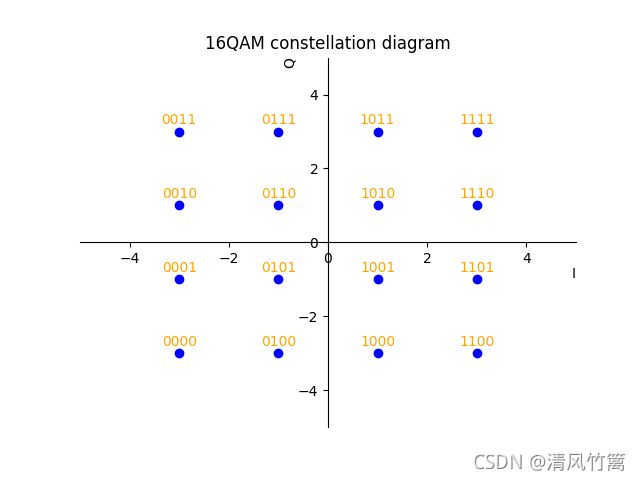
首先将16QAM中比特与振幅的对应关系保存在Python的字典对象diagram中。然后通过for循环遍历出16种不同的比特组合放在变量str种。str中的前两个比特取出来放到str1变量中，查询字典可以得到I路幅值存到变量a中，str中的后两个比特取出来放到str2变量中，查询字典可以得到Q路幅值存到变量b中.有了I路的幅度值和Q路幅度值就可以定位比特组合对应的点的位置了。这里将I路幅度值a和Q路幅度值b保存在Python特有的数据类型一个复数变量complexSpot中。这样16中不同的比特组合就对应了16个不同的复数，每个复数就对应了一个坐标轴里的点的位置。16个比特组合和复数的对应关系作为字典类型保存在了spot中。运行以上程序就得到了16QAM波形图。

观察星座图可以发现16QAM共有三个不同的幅度，12个不同的相位。相邻比特需符合格雷码编码方式。

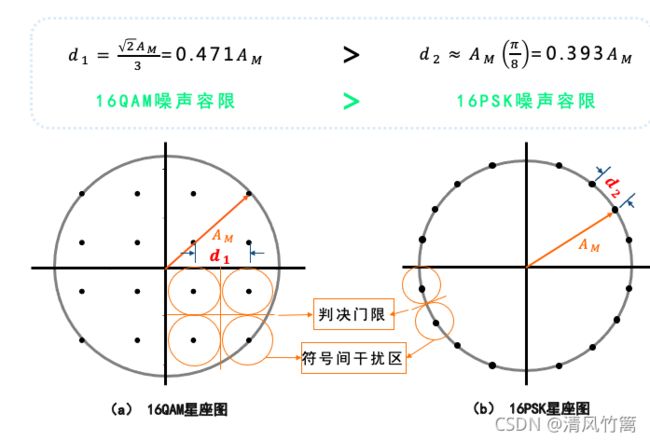
 与16PSK星座图相比较，16QAM星座图中点和点之间的距离较远，这就表示16QAM符号间更加不容易产生相互干扰。通常进制数M增加，会引起误码率的增加。

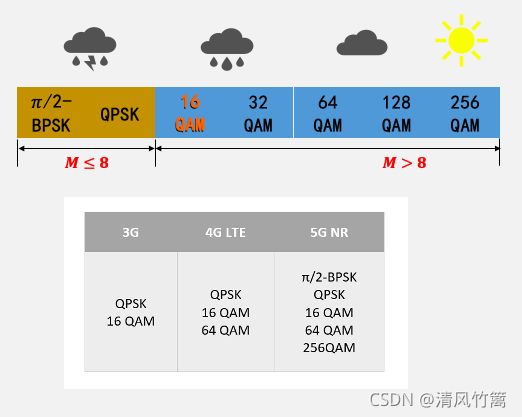
因此在5G网络中，M<=8时采用MPSK;M>8时误码率就会继续增加，从而采用具有更好抗噪声性能的QAM。一般 16QAM是最低阶的QAM。在实际网络中，会根据信道条件相应调整调制方式，信道条件越好，就可以采用越高阶的调制方式。

通过星座图我们也可以详细的看到16种比特组合对应的16个码元波形。

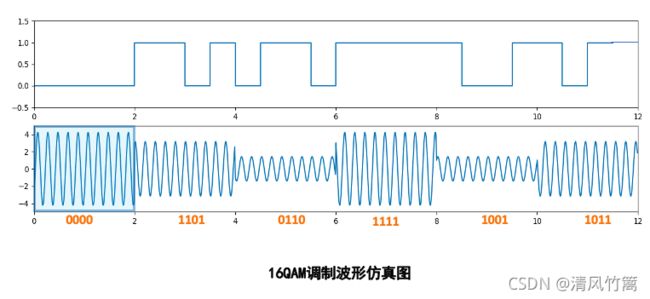
有了16QAM星座图，就有了16种比特组合分别对应的I路和Q路幅度值。接下来就可以将需要进行调制的基带信号的比特流，每四个为一组进行带通信号码元的绘制。由于在绘制星座图的时候就已经保存了比特组合和I路和Q路幅度值的对应关系。因此对于基带信号，只需要每次绘制4个比特，先查询4个比特对应的I路和Q路幅度值，然后分别与两路载波相乘，然后相加就可以得到当前4个比特对应的码元波形了。最后将所有的码元波形都追加到一个列表中，进行图形绘制，就得到了基带信号比特流所对应的带通信号的波形图。

 

import numpy as np
import matplotlib.pyplot as plt

bitsToAmp = {'11': 3, '10': 1, '01': -1, '00': -3}  # 设置数字和幅度的对应关系
spots = {}  # 放置点

for i in ['0', '1']:
    for j in ['0', '1']:
        for k in ['0', '1']:
            for p in ['0', '1']:
                strs = ''.join([i, j, k, p])  # 通过循环获得16个4位数的10组合
                str1 = ''.join([i, j])  # 前两个10组合
                a = bitsToAmp[str1]  # 获取前两个10组合对应的幅值
                a = int(a)

                str2 = ''.join([k, p])
                b = bitsToAmp[str2]
                b = int(b)  # 获取后两个10组合对应的幅值

                complexSpot = complex(a, b)  # 不能写为a+bj，因为编译不通过 生成坐标

                tempSpot = {strs: complexSpot}  # 获得数字组合和点
                spots.update(tempSpot)  # 存入点的集合

fig = plt.figure()
t = np.arange(0, 12.0, 0.5)  # 设置基带信号10的坐标轴，每隔0.5的距离绘制一个基带的二进制信号，一共16个比特

# input
plt.subplot(2, 1, 1)
y1 = [0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1]
plt.plot(t, y1, drawstyle='steps-post')  # 将16个比特每隔0.5绘制到坐标系上
plt.xlim(0, 12)
plt.ylim(-0.5, 1.5)
plt.title('16QAM modulation')

# 串并变换
l4 = int(len(y1) / 4)  # 获取比特流的长度除以4，4个比特为一组，则共有多少组
a = np.asarray(y1)  # 将基带信号转换为numpy格式
y2 = a.reshape(l4, 4)  # 将一维数组转置为二维数组，每一行中有4个比特的数据

plt.subplot(2, 1, 2)
t = np.arange(0, 12., 0.01)  # 横坐标的数据列表，每个0.01绘制一个点
rectwav = []  # 用来存储纵坐标值的列表

# i表示第i个线段，每个线段对应一个二进制的四位组合s0s1s2s3。每个线段的长度为2，是基带信号每个信号长度0.5的四倍
for i in range(l4):
    b = y2[i]  # 取出第i组四位数组合s0s1s2s3
    str4Bits = str(b).strip('[').strip(']').replace(' ', '')  # 将列表中的4个比特转换为字符串并且去掉[ ] 和空格
    complexWave = spots[str4Bits]  # 根据四个比特的字符串对应到字典中的复数，得到横坐标和纵坐标的幅度，I Q的幅度值
    xWave = complexWave.real  # 取出横坐标的值
    yWave = complexWave.imag  # 取出纵坐标的值

    # 在t数组中第i段横坐标的点数，此处每个段的波形长度应该是0.5的4倍，也就是2
    t_tmp = t[(i * 200):((i + 1) * 200)]
    xI_tmp = xWave * np.ones(200)  # 200个横坐标的幅度值
    yQ_tmp = yWave * np.ones(200)  # 200个纵坐标的幅度值
    # 将幅度分别与两个正交载波相乘求和
    wav_tmp = xI_tmp * np.cos(2 * np.pi * 5 * t_tmp) - yQ_tmp * np.sin(2 * np.pi * 5 * t_tmp)
    rectwav.append(wav_tmp)  # 将调制后的点加到总的波形列表中

# 绘制调制后的波形
plt.plot(t, np.array(rectwav).flatten())
plt.xlim(0, 12)
plt.ylim(-5, 5)

plt.tight_layout()
plt.show()

通过波形图可以观察到16QAM每个码元对应4个比特，不同比特组在振幅和相位上都有不同变化。