LDA和SVM练习
LDA和SVM练习
- 一、LDA
- 二、LDA的代码实现(使用sklearn)
- 三、SVM
- 四、SVM的代码实现(月亮数据集)
-
- 1. 使用线性核
- 2. 多项式核
- 3. 高斯核
- 五、SVM的代码实现(鸢尾花数据集)
- 六、总结
- 参考
一、LDA
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
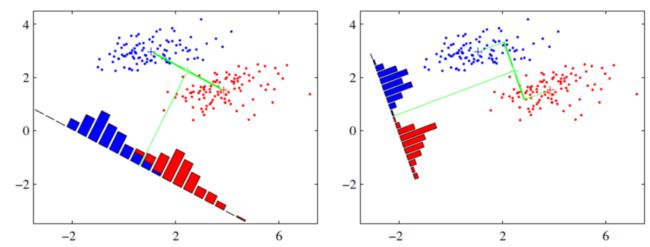
假设我们有两类数据 分别为红色和蓝色,如下图所示,这些数据特征是二维的,我们希望将这些数据投影到一维的一条直线,让每一种类别数据的投影点尽可能的接近,而红色和蓝色数据中心之间的距离尽可能的大。
上图中国提供了两种投影方式,哪一种能更好的满足我们的标准呢?从直观上可以看出,右图要比左图的投影效果好,因为右图的黑色数据和蓝色数据各个较为集中,且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了,当然在实际应用中,我们的数据是多个类别的,我们的原始数据一般也是超过二维的,投影后的也一般不是直线,而是一个低维的超平面。
二、LDA的代码实现(使用sklearn)
训练数据集:
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as lda#导入LDA算法
from sklearn.datasets._samples_generator import make_classification #导入分类生成器
import matplotlib.pyplot as plt #导入画图用的工具
import numpy as np
import pandas as pd
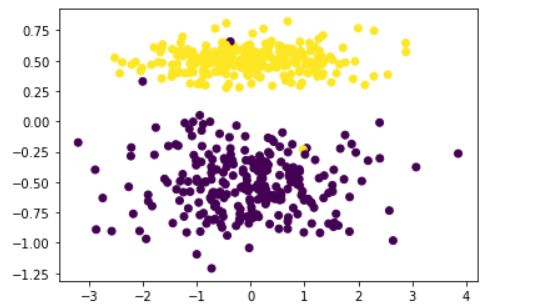
x,y=make_classification(n_samples=500,n_features=2,n_redundant=0,n_classes=2,n_informative=1,n_clusters_per_class=1,class_sep=0.5,random_state=100)
"""
n_features :特征个数= n_informative() + n_redundant + n_repeated
n_informative:多信息特征的个数
n_redundant:冗余信息,informative特征的随机线性组合
n_repeated :重复信息,随机提取n_informative和n_redundant 特征
n_classes:分类类别
n_clusters_per_class :某一个类别是由几个cluster构成的
"""
plt.scatter(x[:,0],x[:,1], marker='o', c=y)
plt.show()
x_train=x[:60, :60]
y_train=y[:60]
x_test=x[40:, :]
y_test=y[40:]
将数据集以6:4的比例分为训练集和测试集,训练:
#分为训练集和测试集,进行模型训练并测试
x_train=x[:300, :300]
y_train=y[:300]
x_test=x[200:, :]
y_test=y[200:]
lda_test=lda()
lda_test.fit(x_train,y_train)
predict_y=lda_test.predict(x_test)#获取预测的结果
count=0
for i in range(len(predict_y)):
if predict_y[i]==y_test[i]:
count+=1
print("预测准确个数为"+str(count))
print("准确率为"+str(count/len(predict_y)))
三、SVM
支持向量机(support vector machines)是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。由简至繁的模型包括:
当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机;
四、SVM的代码实现(月亮数据集)
1. 使用线性核
导入包并展示数据:
# 导入月亮数据集和svm方法
#这是线性svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import StandardScaler
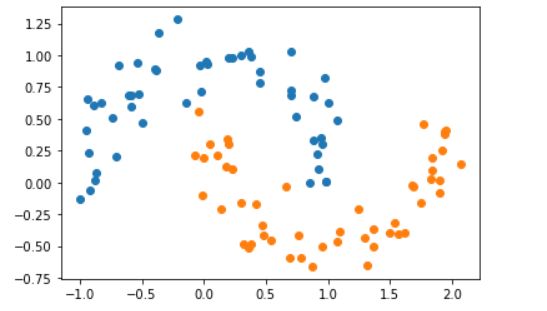
data_x,data_y=datasets.make_moons(noise=0.15,random_state=777)#生成月亮数据集
# random_state是随机种子,nosie是方
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别,并且只取前两个特征
plt.show()
进行标准化训练并画图:
scaler=StandardScaler()# 标准化
scaler.fit(data_x)#计算训练数据的均值和方差
data_x=scaler.transform(data_x) #再用scaler中的均值和方差来转换X,使X标准化
liner_svc=LinearSVC(C=1e9,max_iter=100000)#线性svm分类器,iter是迭达次数,c值决定的是容错,c越大,容错越小
liner_svc.fit(data_x,data_y)
# 边界绘制函数
def plot_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
# meshgrid函数是从坐标向量中返回坐标矩阵
x_new=np.c_[x0.ravel(),x1.ravel()]
y_predict=model.predict(x_new)#获取预测值
zz=y_predict.reshape(x0.shape)
custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0,x1,zz,cmap=custom_cmap)
#画图并显示参数和截距
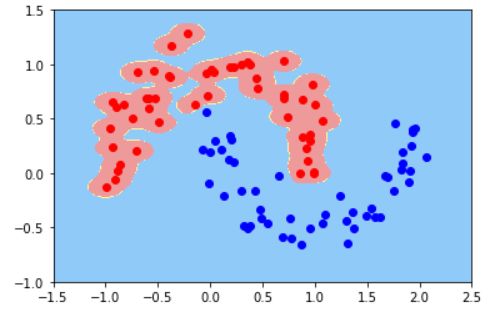
plot_decision_boundary(liner_svc,axis=[-3,3,-3,3])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(liner_svc.coef_)
print('模型截距')
print(liner_svc.intercept_)
2. 多项式核
# 导入月亮数据集和svm方法
#这是多项式核svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from sklearn.pipeline import Pipeline #导入python里的管道
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler,PolynomialFeatures #导入多项式回归和标准化
data_x,data_y=datasets.make_moons(noise=0.15,random_state=777)#生成月亮数据集
# random_state是随机种子,nosie是方
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1])
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1])
data_x=data_x[data_y<2,:2]#只取data_y小于2的类别,并且只取前两个特征
plt.show()
def PolynomialSVC(degree,c=10):#多项式svm
return Pipeline([
# 将源数据 映射到 3阶多项式
("poly_features", PolynomialFeatures(degree=degree)),
# 标准化
("scaler", StandardScaler()),
# SVC线性分类器
("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42,max_iter=10000))
])
# 进行模型训练并画图
poly_svc=PolynomialSVC(degree=3)
poly_svc.fit(data_x,data_y)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])#绘制边界
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(poly_svc.named_steps['svm_clf'].coef_)
print('模型截距')
print(poly_svc.named_steps['svm_clf'].intercept_)
3. 高斯核
## 导入包
from sklearn import datasets #导入数据集
from sklearn.svm import SVC #导入svm
from sklearn.pipeline import Pipeline #导入python里的管道
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler#导入标准化
def RBFKernelSVC(gamma=1.0):
return Pipeline([
('std_scaler',StandardScaler()),
('svc',SVC(kernel='rbf',gamma=gamma))
])
svc=RBFKernelSVC(gamma=100)#gamma参数很重要,gamma参数越大,支持向量越小
svc.fit(data_x,data_y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')#画点
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
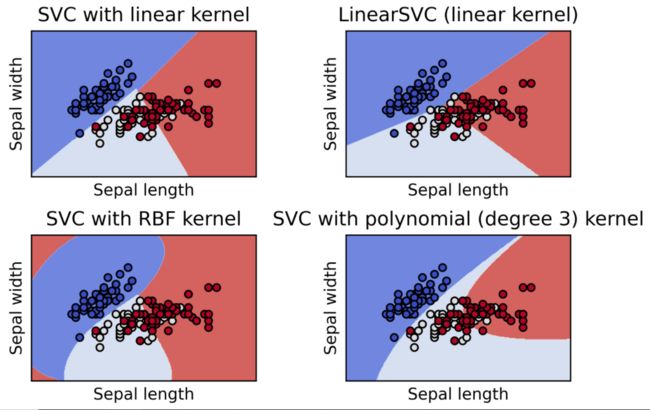
五、SVM的代码实现(鸢尾花数据集)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# 定义网格函数
def make_meshgrid(x, y, h=.02):
"""Create a mesh of points to plot in
Parameters
----------
x: data to base x-axis meshgrid on
y: data to base y-axis meshgrid on
h: stepsize for meshgrid, optional
Returns
-------
xx, yy : ndarray
"""
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))
return xx, yy
# 绘制填充颜色的二维等高线图_
def plot_contours(ax, clf, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Parameters
----------
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
# np.c_中的c是column的缩写,是按列叠加两个矩阵的意思,就是把两矩阵左右相加
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
# import some data to play with
iris = datasets.load_iris()
# Take the first two features. We could avoid this by using a two-dim dataset
X = iris.data[:, :2]
y = iris.target
# we create an instance of SVM and fit out data. We do not scale our data since we want to plot the support vectors
C = 1.0 # SVM regularization parameter
models = (svm.SVC(kernel='linear', C=C),
svm.LinearSVC(C=C, max_iter=10000),
svm.SVC(kernel='rbf', gamma=0.7, C=C),
svm.SVC(kernel='poly', degree=3, gamma='auto', C=C))
models = (clf.fit(X, y) for clf in models)
# title for the plots
titles = ('SVC with linear kernel',
'LinearSVC (linear kernel)',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel')
# Set-up 2x2 grid for plotting.
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
plt.rcParams['savefig.dpi'] = 600 #图片像素
plt.rcParams['figure.dpi'] = 600 #分辨率
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
for clf, title, ax in zip(models, titles, sub.flatten()):
plot_contours(ax, clf, xx, yy,cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
六、总结
线性判别的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,异样样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的直线上,再根据投影点的位置来确定新样本的类别。
参考
线性判别分析LDA原理总结
LDA与SVM实践(python实现)
线性判别准则与线性分类