并行计算-稠密矩阵计算复习（待续--待补一块内容和Cannon，DNS，Fox算法）

基本的矩阵乘法分析

对于矩阵乘法运算，代码写得多的人一定感觉亲切且熟悉。
一定是i，j，k三重循环，时间复杂度高达O(n³)。
那么学习过strassen矩阵链乘法的应该知道复杂度能降到O(n^2.8)。

基于并行计算的矩阵乘法运算

其实感觉并行计算和分治的思想有相似的地方，都是不断划分成小问题后进行综合求解。

矩阵划分方式
既然我们知道要对大问题进行划分，那么划分方法必然是值得讨论的一环。

带状划分
1.块带状划分
2.循环带状划分
3.块状循环划分

由上图可知，块状划分是我们一开始就算好的。
比如上图有4个Processor（处理器），矩阵大小是16 × 16，那么一块就可以是：
4 × 16的子矩阵或者可以是16 × 4的子矩阵，无非是按照行或列划分的不同之处。
这种划分优点在于简单易实现代码较为容易，缺点也很明显，如果不能平均划分的话最后一个处理器会处理较多的数据。
比如32个处理器，60 × 60的矩阵，前31个处理器每个处理1行，那么最后一个就得处理29行！！这显然对于最后时间影响是很大的。

循环划分显然解决了上面块状划分的缺点，其思想就是（假如有4个处理器）：第1行给第一个处理器处理，第2行给第二个处理器……到第5行后又给到第一个处理器处理。这样一来，那么即使是处理最多任务数的处理器也只是比其余的多出一个任务而已。

块状循环划分就是两者的综合，比如以3行为一次的话，那么第13行开始的后三行又交还给第一个处理器进行运算（假设是4个处理器）。

这儿……没代码，没写过。【可能会补】

棋盘划分
1.块棋盘划分
2.循环棋盘划分
3,循环块状棋盘划分

从上图看很清晰，块状划分就是这么多2 × 2的子矩阵。
循环划分，0行-3行按序往下处理，到4行时又回交给第一行的处理器处理。感觉语言描述不清楚，看图还是好理解的。

矩阵转置

网孔上的矩阵转置
当p = n²时，通信方式如下。对角线上的数据显然是不用改变的，其余的，比如P1，发送给P5再给P4。P4就是先发送给P0再给P1，完成交换。

当然了很多情况下我们的处理器数远远达不到这么多，那么示意图如下所示（假设是 n × n的矩阵，处理器矩阵是 p^1/2 × p^1/2）：

这种情况下的矩阵转置我们分两步走，第一步同 p = n²，只不过交换的元素是一个子矩阵而不像上面就是单纯的一个元素，也就是我们的图a。
第二步是子矩阵内部的对角交换，也就是图b。
可以自行模拟试试看，是不是真的转过来了。

对此我们要熟悉其时间。不然怎么知道并行计算比串行好在哪？
这里先不进行对通信时间分析计算的仔细复习，先利用一下结论即可。

下图就是存储转发(SF)的时间计算公式。

注：其中，ts是启动时间不可省略，tw是单个字的传输时间，显然的m就是信包长度，th是延迟时间，l是链路长度。

a图中我们易知最长的链路长度就是从右上角到左下角，共2×p^1/2链路长度。我们忽略th延迟时间，m作为信包长度就是我们的一个子块矩阵的大小，就是n²/p。
而在b图中我们进行矩阵内部的转置，假设成对元素局部交换取单位时间，那么现在子矩阵大小是n²/p，又因为我们只交换一半元素，所以就是1/2 × n²/p。
把上述两部分时间相加自然就得到下面的结论了。

超立方上的矩阵转置

带状划分的矩阵转置

矩阵向量乘法

对于单处理机来讲，这个算法的效率较好分析。
第一重循环控制矩阵的行，第二重循环就是控制矩阵的列也就是向量的下标。
好，那么很容易得出时间复杂度为O(n²)。

带状划分的矩阵向量乘法

具体思路如下图所示：
每个处理器除了拥有当前矩阵的一行，还拥有x[i]即向量的第i个元素。
那么我们第一步要做的就是将向量元素进行一个广播操作，是多对多播送，如b图所示，那么矩阵中的每个元素都会得到自己要乘的目标！
c图就是简单的乘法操作，d图就是一个求和归约操作。
[单处理器的归约求和，不能直接套O(logn)的并行归约时间复杂度！]。
此种方式通信和计算的时间复杂度都是O(n)，

上述是p == n的情况下，加入p < n的话无非就是每个处理器处理n / p行而已。

超立方的矩阵向量乘法
超立方形式的网络，进行多到多播送，先直接套用计算结果：
参数含义和上面解释过的是一样的，具体是个什么意思还是先不赘述，后面复习第二章时会一个个推导过来。哦对了，p就是处理器数

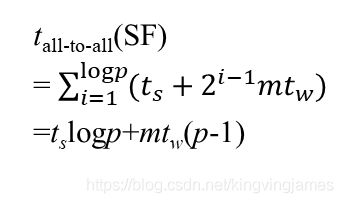
现在我们的m作为字长就是我们需要广播的n/p个向量元素，带入即可。
试想当p足够大时，p - 1近似就是p，那么得到的解就是：

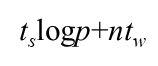
每个处理器管理的子矩阵大小是 n / p × n，所以实际上还要花费 n²/p的时间用于乘-加运算。所以得到超立方上带状划分矩阵向量计算时间为：

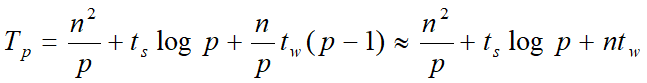
网孔上的矩阵向量乘法
仍旧先利用一个结论：

同样是基于此结论，进行近似操作和乘-加操作时间求和得到的结果如下：

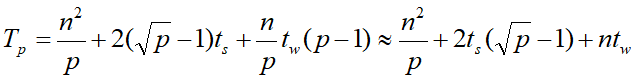
棋盘划分的矩阵向量乘法

其操作示意图是如下所示的：

上图是假设p == n²情况的。
我们首先需要一次一对一的通信将向量元素放到矩阵的主对角线上。
然后和上面的带状一致进行一次一对多的通信将向量元素都广播出去。
c图做得就是乘-加运算和单点累积。此步操作时间为O(n)但对于超立方来说是O(logn)，所以最后：
在网孔上的时间为O(n)，超立方上的时间就是O(logn)。

再考虑 p < n²的情况：
仍旧是将处理器矩阵视为是 p^1/2 × p^1/2的矩阵，每个处理器存放 n / p^1/2 × n / p^1/2大小的矩阵。
处理器矩阵最后一列存放对应的向量元素。
第一步：
对准操作，利用CT选路法进行一对一的传播，时间如下：
只需把m用 n / p^1/2带入，l则用最长链路长度p^1/2带入。

第二步：
按列进行一对多播送。
同样，m用n / p^1/2替换。
以下公式是由矩阵中的一个元素广播给所有！现在我们仅需列广播，仅需此的1/2
即可！！最后加的时候别搞错就行！

第三步：
单点累积操作。
这一步的操作和上一步的时间是一样的也可以视为将自己的值广播给其他处理器以供加法操作。

最后不能忘了乘-加运算的时间，如果一次视为单位时间，那么此时子矩阵大小n/p²直接就是运算时间。

所以最后二维网孔上CT选路的总时间为：

当然也可以采用SF选路方式，最后的答案如下：

矩阵乘法

ATTENTION!这里是大头！
以下是自己简单的一份带状划分的矩阵乘法Cpp代码，仅供参考，代码解释跟在代码后面。此分块比较简单，因为有一个矩阵没被分块。

#include "mpi.h"
#include 
#include 
using namespace std;
int main(int argv, char *argc[])
{
     
	const int n = 1000;
	int rank, p;
	MPI_Init(&argv, &argc);
	MPI_Comm_rank(MPI_COMM_WORLD, &rank);
	MPI_Comm_size(MPI_COMM_WORLD, &p);
	MPI_Status status;
	int NUM = floor(1000.0 / p);    // 每个处理器要处理的行数（不一定完全除尽，比如64个处理器。于是会先另NUM = 15， 1000 - 63 × 15 = 55剩下的任务全部令P0完成）
	double* buff = new double[NUM * n + 100];   // 接受方处理器的缓冲区
	double* ans = new double[NUM * n + 100];    // 计算返回值　
	double* matrix = new double[n * n];         // matrix用于接收A × B中的B矩阵
	if (rank == 0)
	{
     
		double(*A)[n] = new double[n][n];
		double(*B)[n] = new double[n][n];
		double(*C)[n] = new double[n][n];
		double(*D)[n] = new double[n][n];
		for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
		{
     
			A[i][j] = rand()*1.0 / RAND_MAX;
			B[i][j] = rand()*1.0 / RAND_MAX;
		}
		if (p == 1)
		{
     
			double tb, te;
			tb = MPI_Wtime();
			for (int i = 0; i < n; i++)
			{
     
				for (int j = 0; j < n; j++)
				{
     
					C[i][j] = 0;
					for (int k = 0; k < n; k++)
						C[i][j] += A[i][k] * B[k][j];
				}
			}
			te = MPI_Wtime();
			cout << "time is " << te - tb << "s" << endl;
		}
		else{
     
			double ta, tb;
			ta = MPI_Wtime();
//使用广播机制，把右乘的B矩阵广播到其余的所有进程
			MPI_Bcast(B[0], n * n, MPI_DOUBLE, 0, MPI_COMM_WORLD);			
for (int i = 1; i < p; i++){
     
				MPI_Send(A[(i - 1) * NUM], NUM * n, MPI_DOUBLE, i, 10, MPI_COMM_WORLD);   // 消息传递 行头 + 处理个数（行数 * 列数） 
			}
			for (int i = 1; i < p; i++){
     
				MPI_Recv(ans, NUM * n, MPI_DOUBLE, i, 20, MPI_COMM_WORLD, &status);// 得到NUM行的计算结果
				int k = 0;  // k用于计数接受到的答案ans的行数，因为ans始终是NUM行，跟随C的写入逐行递增。
// 由于处理器从 1～p – 1依次处理NUM行，从第0行开始。所以j的循环如下
				for (int j = (i - 1) * NUM; j < i * NUM; j++){
     
					for (int l = 0; l < n; l++){
     
						C[j][l] = ans[k * n + l];
					}
					k++;
				}
			}
// 由主进程P0来处理从（p-1）×NUM行直到最后一行的数据
			for (int i = (p - 1) * NUM; i < n; i++){
     
				for (int j = 0; j < n; j++){
     
					C[i][j] = 0;
					for (int k = 0; k < n; k++){
     
						C[i][j] += A[i][k] * B[k][j];
					}
				}
			}
			tb = MPI_Wtime();
			cout << "parrallel time is " << tb - ta << "s" << endl;
		}
		
// tc, tb用于记录串行的时间， 串行运行的结果矩阵存储在D中
		double tc, td;
		tc = MPI_Wtime();
		for (int i = 0; i < n; i++)
		{
     
			for (int j = 0; j < n; j++)
			{
     
				D[i][j] = 0;
				for (int k = 0; k < n; k++)
					D[i][j] += A[i][k] * B[k][j];
			}
		}
		td = MPI_Wtime();
		cout << "time is " << td - tc << "s" << endl;

		// 用于比较的测试代码，比较简单就不赘述
		bool flag = true;
		for (int i = 0; i < n; i++){
     
			for (int j = 0; j < n; j++){
     
				if (C[i][j] != D[i][j]){
     
					cout << i << " " << j << endl;
					cout << C[i][j] << " " << D[i][j] << endl;
					flag = false;
					break;
				}
			}
			if (!flag)
				break;
		}
		cout << boolalpha << flag << endl;
		delete[] A;
		delete[] B;
		delete[] C;
		delete[] D;
		
	}
//由于以上二维矩阵的创建方式是连续的，可用一维矩阵来接受
	else{
     
		MPI_Bcast(matrix, n * n, MPI_DOUBLE, 0, MPI_COMM_WORLD);
		MPI_Recv(buff, n * NUM, MPI_DOUBLE, 0, 10, MPI_COMM_WORLD, &status);
// matrix[k*n+j]相当于在二维矩阵中取B[k][j],buff[i*n+k]实际上就是A[i][k]
		for (int i = 0; i < NUM; i++){
     
			for (int j = 0; j < n; j++){
     
				ans[i * n + j] = 0;
				for (int k = 0; k < n; k++){
     
					ans[i * n +j] += buff[i * n + k] * matrix[k * n + j];
				}
			}
		}
		MPI_Send(ans, NUM * n, MPI_DOUBLE, 0, 20, MPI_COMM_WORLD);
	}
	MPI_Finalize();
	return 0;
}
代码解释：
在改变原提供代码不变的基础上进行添加。
首先根据进程个数划分每个进程要处理的行数NUM。

如：
32个进程，1000行，则每个进程需要处理31.25，显然浮点是不合适的，于是取31。
这样会导致，除了主进程以外的31个进程，每人处理31行，共961行，则剩下的39行全部由P0主进程完成！


主进程会把需要右乘的矩阵B（计算A × B的结果）用MPI_Bcast广播机制令其余的进程也都能接收到。
由于据上所述每个处理器处理NUM行，则如P1处理器，则是从0～NUM-1行的数据。
所以Send消息传递给每个处理器都是从(i - 1)*NUM行首地址开始传，共NUM × n个数据。

（由于源代码中的二维矩阵的创建方式是连续的所以换做一维矩阵接收）
其余进程负责计算，要先接受A中的NUM行数据和整个B矩阵。
把两个一维的重新想象为二维的，对buff中的NUM行，每行都去乘上完整的B矩阵。
得到的ans实际上就是答案。
然后把ans放回。

主进程中要重新进行拼装。
同样是根据第i个进程负责的是第（i - 1）×NUM～i×NUM行这个规律进行填充。
值得注意的是主进程收到的答案ans始终只有NUM行，我们需要用一个递增的k（表示ans的行号）来跟进填充。

剩下的没被计算完的行数全部由P0负责完成！

并行分块算法
要写的话实在太多直接copy老师的ppt了，最重要的还是理解啦。

比如一个分好块的矩阵长这样：
就是上面说的P_i,j处理器保存的是A和B的子块。
但这张图不好的地方就在于每个子矩阵刚好只有一个元素了就是p == n²，我们上面讨论的情况更加具有普适性。
子矩阵大小应该是 n / p^1/2 × n / p^1/2。

好了现在需要知道整个乘法流程怎么走，缺什么才能得到正确答案。
【这样才可以确定通信的内容】

比如我们要求C_{0, 0}，以上图为示，我们需要知道第一行处理器的所有A元素和第一列处理器的所有B元素，然后对应相乘求和得到第一个子块的答案！

正因如此，我们才需要算法中的第一步通信！即A矩阵的行方向上的多对多通信和B矩阵的列方向上的多对多通信。

乘加运算是比较好理解的，不再赘述。

下式是超立方多对多通信的解：
当然了这里需要按需进行一些修改，不能是logp，得是1/2logp（因为一行只有p^1/2个处理器），m的话就是n²/p大小，而最后显然是需要乘上2，因为A和B都需要通信。

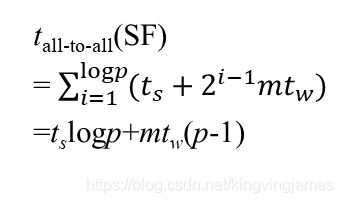
最后还需要加上计算时间，因为子块与子块的矩阵运算仍旧是通过串行来完成的，又因为子矩阵边为n/p_1/2，所以自然是其3次方，又因为需要p_1/2块子矩阵累加才会得到最终解所以还要乘上这个数！

对于二维网孔分析是类似的，如下所示：