李沐《动手学深度学习》 笔记（二）用pytorch实现线性回归

有关线性回归的数学基础，可以看这里linear regression，书上讲的很清楚~

值得一提的是，线性回归问题是有全局最优解的

解析解为：

但这里采用迭代法进行优化

稍微改了改代码，实现了部分数据的可视化

 

导入需要的包 

import torch
import matplotlib.pyplot as plt
import numpy as np
from torch.utils import data
from d2l import torch as d2l

第一步，获取数据集

true_w = torch.tensor([2, -3.4])
true_b = torch.tensor(4.2)
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

synthetic_data函数说明

这里也可以用d2l.synthetic_data？或者d2l.synthetic_data？？来查询函数相关信息

如果用两个问号，可以查看函数的具体实现代码

help(d2l.synthetic_data)

 查看输入特征

print(features.shape)
print(labels.shape)
plt.plot(features[:, 0], features[:, 1], '.')

在三维坐标系中查看该数据集 

from mpl_toolkits.mplot3d import Axes3D
a = torch.cat([features, labels], axis=1)
fig = plt.figure(figsize=(12, 8))
ax = Axes3D(fig)
ax.scatter(a[:,0], a[:, 1], a[:, 2])

 

第二步，读取数据集，建立数据迭代器

data_xy = (features, labels)
dataset = data.TensorDataset(*data_xy)
data_iter = data.DataLoader(dataset, batch_size=16, shuffle=True)

第三步，搭建网络，初始化网络参数

from torch import nn
net = nn.Sequential(nn.Linear(2, 1))
net[0].weight.data.normal_(0, 0.02)
net[0].bias.data.fill_(0)

第四步，定义损失函数

loss = nn.MSELoss()

第五步，定义优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.01)

第六步，开始训练

epochs_num = 3
for epoch in range(epochs_num):
    for x, y in data_iter:
        l = loss(net(x), y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print('epoch:{}, loss:{}'.format(epoch+1, l))

第七步，训练结果可视化

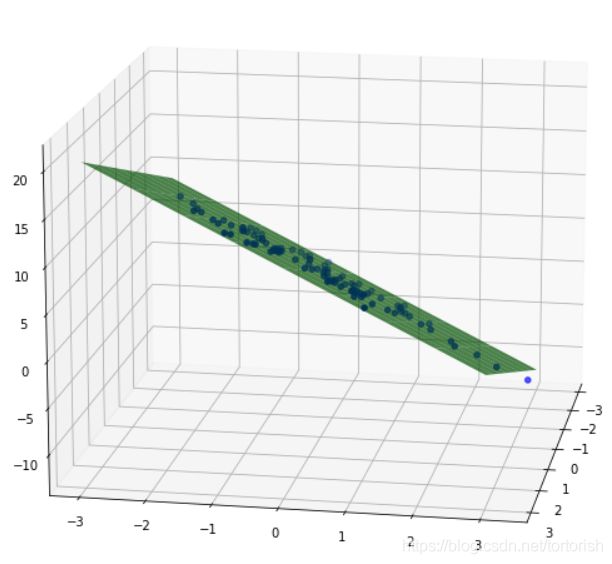
fig = plt.figure(figsize=(10, 6))
ax = Axes3D(fig)
ax.scatter(features[0:100, 0], features[0:100, 1], labels[0:100], color='blue')
x = np.linspace(-3, 3, 9)
y = np.linspace(-3, 3, 9)
X, Y = np.meshgrid(x, y)
ax.plot_surface(X=X,
    Y=Y,
    Z=1.9992*X-Y*3.4001+4.1988,
    color='green',
    alpha=0.7
    )
ax.view_init(elev=15,
             azim=10)

绿色的平面就是得到的结果，由于数据量较大且网络参数少，所以训练三个epoch以后，平面就能很好的拟合原始的特征！