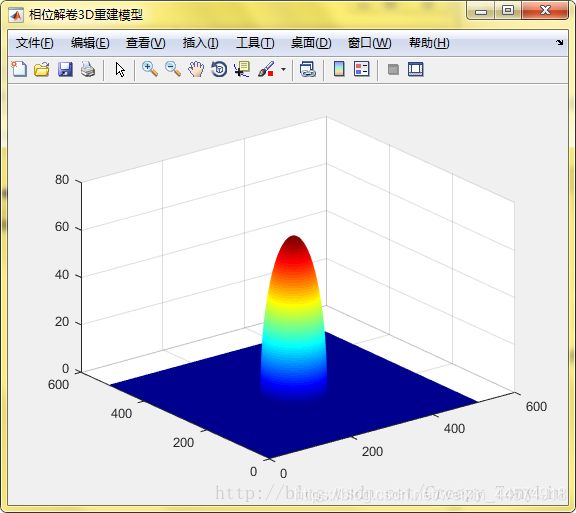
基于结构光的相移法三维重建

提笔先致谢!
基于结构光的相移法三维重建
由于正在学习条纹结构光扫描相关知识，就发现了这篇很棒的博客，特此分享，并致谢原作者：（博客园）创造卓越人生 。

一、基本原理：

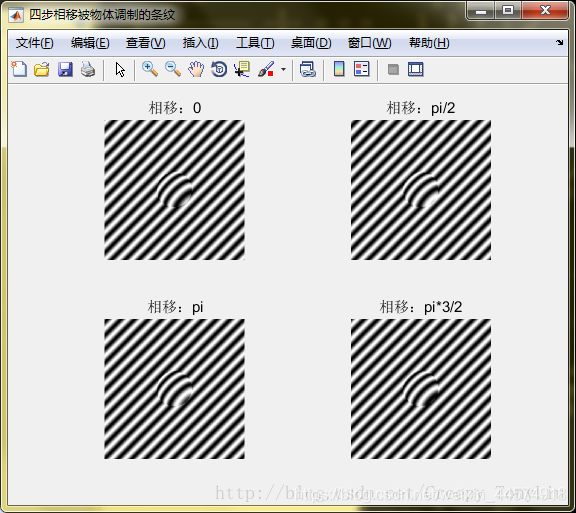
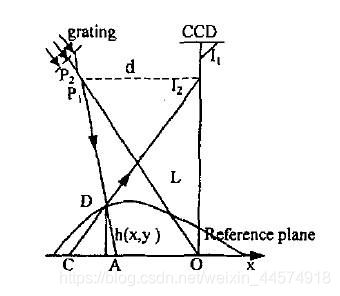
正弦条纹打在三维物体上，CCD记录到的条纹由于受到三维物体高度的调制而发生扭曲，扭曲的条纹（deformed fringe）实质上为原始条纹在物体具有高度存在的位置有了附加相位，各点的相位表现为由CCD图像采集获得的被调制的条纹数字图像的灰度值。通过扭曲的条纹和原始条纹比对计算得出相位变化值。

又已知投影仪、CCD和物体的具体位置和之间的距离，利用数学关系可求出对应点的高度值，实现3D重建。公式推导如下：（下图来自[1]）

二、四步相移法

获得正确的相位值并计算出相位差是得到物体真实高度信息并进行3D重建的关键。

在利用CCD进行数字采集过程中，由于环境等各种因素的影响，以及物体在空间上对光的反射程度和与CCD距离不同，不能够得到理想的均匀而又高对比度的条纹，也就不能得到最真实的相位信息。

运用四步相移法处理此问题（此方法参考[1]）,过程分析如下：

式中 R(x,y) 表示所测物体表面的不均匀反射率，A(x,y) 是背景强度，B(x,y)/A(x,y) 表示的是光栅条纹的对比度。∅(x,y) 是相位值。

考虑到以上引入的多个外部影响因子，利用四步相移法分别记录四次初相不同的正弦条纹和被调制的条纹（每个相差π/2），联立即可得到消去外部因子的真实相位值。

表达式如下：

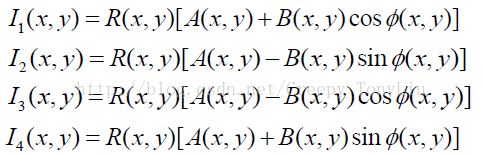
分别为初相等于0、π/2、π 和 3π/2 的条纹表达式，由三角函数变换可分别化成上式
联立解得

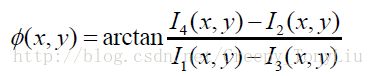
可以看到A、B、R三个外部因子被消去，留下相位的正切值。利用反正切函数即可求出相位分布。

三、包裹相位处理（相位展开/相位解卷）

1、 相位包裹的含义：

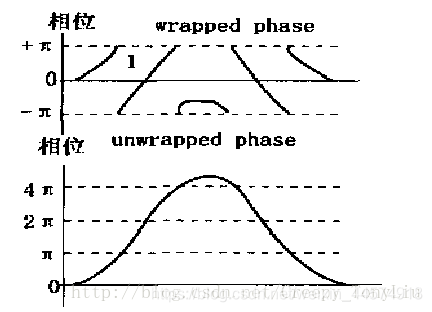
如图所示（图片来自[1]），下图为真实相位值，上图为被包裹的相位。即不在反正切函数(-π,π)的主值区间内的相位值被加上或减去n个2π（n为整数），使其值被调整了主值区间(-π,π)内，称为相位包裹。被包裹的相位（wrapped phase）并不是真正的相位信息，需要进行相位展开，还原出其原始的相位值。
此处有另一个重点，数学中常用的反正切函数是二象限的反正切函数，值域仅是(-π/2,π/2)，而此处我们运用的反正切函数是四象限的反正切函数，值域是(-π,π)。区别如下：
二象限反正切函数（matlab中函数名为atan）输入参数为正切值，返回正切值仅有两个第一第四两个象限的角度值，即(-π/2,π/2)。而四象限反正切函数（matlab中函数名为atan2）输入参数为y和x，返回正切值包括四个象限，即(-π,π)。

四象限反正切考虑到正切值的由来是两个量的商，多考虑了x为负时的另一种情况，即可以将值域扩展一倍，延长到(-π,π)。

表达式如下：（表达式来自Wikipedia）



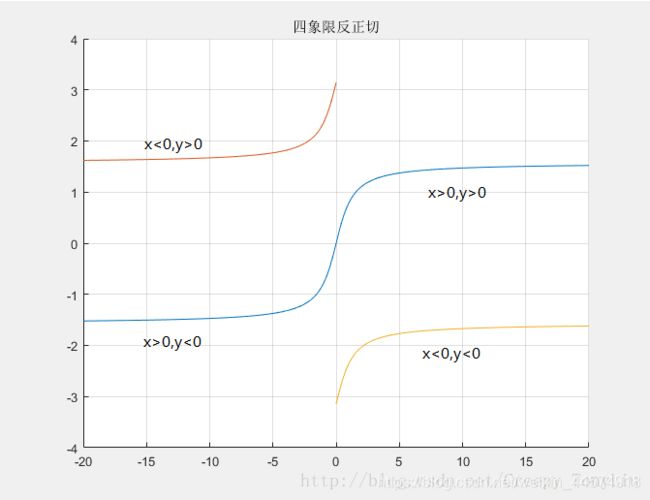
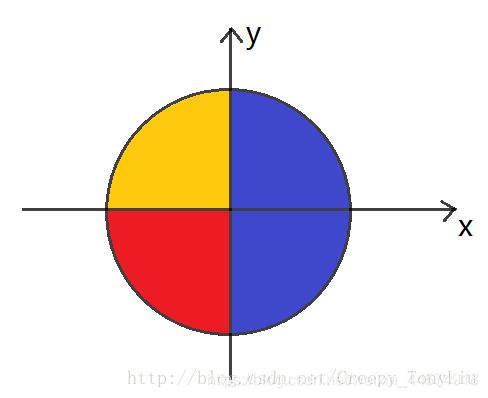
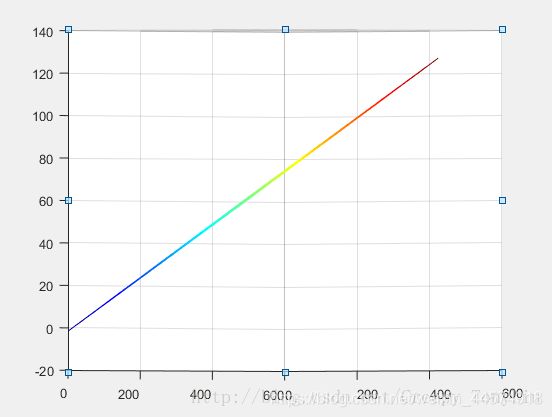
上图为本人用matlab粗略汇出的四象限反正切函数曲线，各条曲线颜色对应下图圆中角所在的区域。

2、解卷/相位展开/相位解包裹操作（phase unwrapping）
上面讲述的相位包裹表现为相位在主值区间内增加到超过主值区间的上限的时候，即超过π时，将发生跳变，也就是说继续增加相位值会跳变到-π。在整体提取的图像中沿着相位增加的方向表现为锯齿波的形状。如下图为没有被物体调制过的条纹沿着条纹的方向横截，

被包裹的相位图：

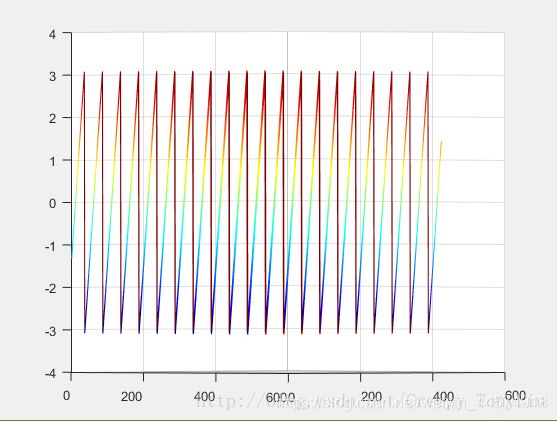
相位展开最根本的思想就是找出相位发生跳变的地方，补上被减去的n个2π，使跳变出相位值和周围的值变得连续、平滑。方法很多，请参考[1]，文中详细讲解质量法。
本次使用matlab仿真直接使用了matlab中相位解卷函数unwrap(P,tol,1)。其中P为执行相位解卷的向量或矩阵；tol为相位跳变限度（jump tolerance），即差值大于tol被判定为发生跳变，默认为pi，此处我使用的时候填pi；第三个参数表示进行相位解卷操作的维度，向量只有一个维度，矩阵有两个维度，则1表示行解卷，2表示列解卷。上一张图相位展开完成后相位分布如下图，
可以看到不存在跳变（锯齿）。

四、傅里叶变换法还原相位

运用此方法不进行相位解卷便可以获得真实的相位信息。原理如下：（此方法和原理公式来自[2]）

被包裹的相位表示为

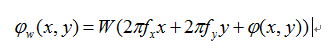
其中φ(x,y)为真实的相位信息，fx和fx标志条纹频率。
将被包裹的相位表示成复数形式

二维傅里叶变换

频移后进行逆傅里叶变换

求复数表示的相位的相角即可得到真实相位值

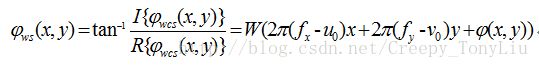
两次傅里叶变换亦可以应用傅里叶变换的频移性质实现：

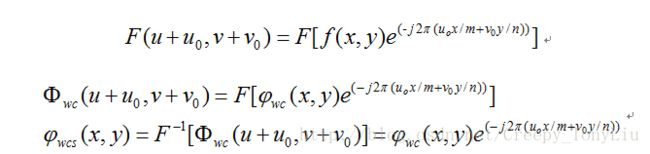
此方法就是利用傅里叶变换频移实现滤波操作，滤掉条纹部分的信息。[2]对该方法提高精度的一些办法进行了阐述，具体参考原文。
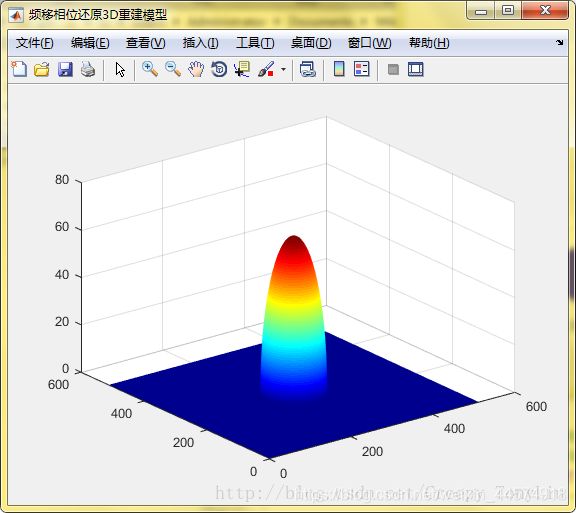
此方法虽然可以直接得到相位信息而不需要进行解卷，且精度较高，但是因为没有解卷，若物体高度换算大于2π的相位差，则或出现重建变形，较高部分凹陷下去的情况。

五、matlab仿真结果

**

仿真基本可以重建出半球的形状。半球最高点高度理论上应该是半径的长度，由于计算所用的正弦波周期是通过离散傅里叶变换频谱峰值提取出的频率，提取出的频率存在误差。

参考文献：

[1] 潘玉玲. 相移法三维测量系统[D]. 重庆大学, 2013.

[2] Du G, Wang M, Zhou C, et al. Improved method for phasewraps reduction in profilometry[J]. 2016.

六、仿真matlab代码

function my_3D_reconstruction

u = pi/25;
v = pi/25; % 给定初始条纹角频率
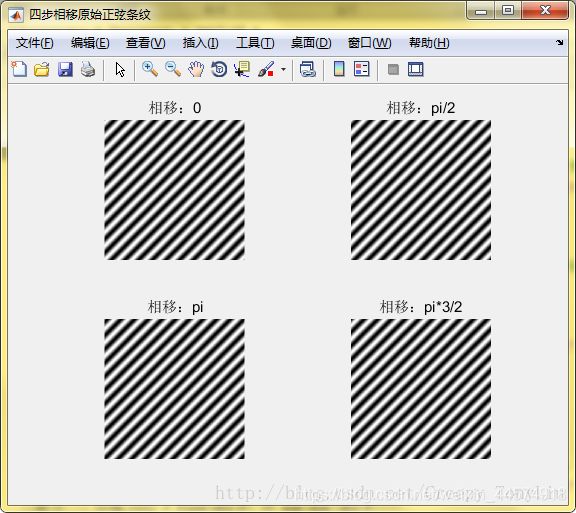
fringe1 = sin_wave(u,v,0);
fringe2 = sin_wave(u,v,pi/2);
fringe3 = sin_wave(u,v,pi);
fringe4 = sin_wave(u,v,pi3/2);
figure(1);
set(gcf,‘Name’,‘四步相移原始正弦条纹’,‘NumberTitle’,‘off’);
subplot(221);imshow(fringe1);title(‘相移：0’);
subplot(222);imshow(fringe2);title(‘相移：pi/2’);
subplot(223);imshow(fringe3);title(‘相移：pi’);
subplot(224);imshow(fringe4);title('相移：pi3/2’);

h = halfball(65,256,256); % 半径150mm 球心坐标（256,256）仿真假设一个像素为1mm
figure(2);
surf(h);
colormap(jet);
set(gcf,‘Name’,‘原半球物体’,‘NumberTitle’,‘off’);
shading interp;

D = 155;
L = 660;
T = 50/sqrt(2); % 参数单位 mm
delta_phi = 2piDh./(L-h)/T; % T为正弦条纹的空间周期
deformed_fringe1 = fringe_modulation(u,v,0,delta_phi); % 生成四步相移的被调制条纹
deformed_fringe2 = fringe_modulation(u,v,pi/2,delta_phi);
deformed_fringe3 = fringe_modulation(u,v,pi,delta_phi);
deformed_fringe4 = fringe_modulation(u,v,pi3/2,delta_phi);
figure(4);set(gcf,‘Name’,‘四步相移被物体调制的条纹’,‘NumberTitle’,‘off’);
subplot(221);imshow(deformed_fringe1);title(‘相移：0’);
subplot(222);imshow(deformed_fringe2);title(‘相移：pi/2’);
subplot(223);imshow(deformed_fringe3);title(‘相移：pi’);
subplot(224);imshow(deformed_fringe4);title(‘相移：pi*3/2’);

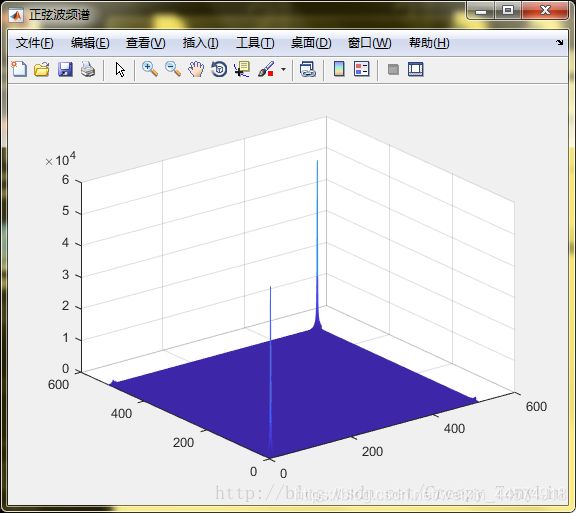
F = fft2(fringe1-0.5); % 傅里叶变换检测峰值提取正弦条纹的空间频率fx、fy
figure(3);
mesh(abs(F));
set(gcf,‘Name’,‘正弦波频谱’,‘NumberTitle’,‘off’);
[row,col] = find(abs(F) == max(max(abs(F))));
fx = (row(1)-1)/512;
fy = (col(1)-1)/512;
Tx = fx^(-1);
Ty = fy^(-1); % 提取出正弦条纹的频率,换算成空间周期
T1 = Tx*Ty/sqrt(Tx^2+Ty2);

wrapped_phase = atan2((deformed_fringe4-deformed_fringe2),(deformed_fringe1-deformed_fringe3));
original_phase = atan2((fringe4-fringe2),(fringe1-fringe3));
%相位包裹的被调制的条纹和原始条纹计算

%----------傅里叶变换频移法还原相位------------------------------------------
k = exp(1iwrapped_phase);
[x,y] = meshgrid(1:512,1:512);
k = k.exp(-21ipi*(fxx+fyy));
k = atan2(imag(k),real(k));

f = exp(1ioriginal_phase);
[x,y] = meshgrid(1:512,1:512);
f = f.exp(-21ipi*(fxx+fyy));
f = atan2(imag(f),real(f));

p = k-f;
high = LT1p./(2piD+T*p);
figure(6);
set(gcf,‘Name’,‘频移相位还原3D重建模型’,‘NumberTitle’,‘off’);
surf(high);
colormap(jet);
shading interp;
%--------------------------------------------------------------------------
%-----------相位展开还原相位------------------------------------------------
unwrapped_org= unwrap(original_phase,pi,2); % 衬底列解卷
unwrapped_org= unwrap(unwrapped_org,pi); % 衬底行解卷

unwrapped_phase= unwrap(wrapped_phase,pi,2); % 物体列解卷
unwrapped_phase= unwrap(unwrapped_phase,pi); % 物体行解卷

delta = unwrapped_phase-unwrapped_org; % 相位差
H = LT1delta./(2piD+T*delta); % 计算高度
figure(5);
set(gcf,‘Name’,‘相位解卷3D重建模型’,‘NumberTitle’,‘off’);
surf(H);
colormap(jet);
shading interp;
%--------------------------------------------------------------------------

function output = halfball(r,x,y) % 半球绘制函数
temp = zeros(512);
for m = 1:512
for n = 1:512
if((m-x)^2 + (n-y)^2 < r^2)
temp(m,n) = sqrt(r^2 - (x-m)^2 - (y-n)^2);
end
end
end
output = temp;
end

function output = fringe_modulation(u,v,phi,delta_phi) % 物体产生相移条纹函数(x频率，y频率，原条纹初相，相移量)
for a = 1:512
for b = 1:512
img(a,b) = (1+sin(ua+vb+delta_phi(a,b)+phi))/2;
end
end
output = img;
end

function output = sin_wave(u,v,phi) % u、v为角频率,phi为初相
for m = 1:512
for n = 1:512
temp(m,n) = (1+sin(um+vn+phi))/2;
end
end
output = temp;
end
end