数值计算：高斯-勒朗德积分公式

高斯-勒朗德积分公式

高斯-勒朗德积分原理参考《数值分析》第五版P188

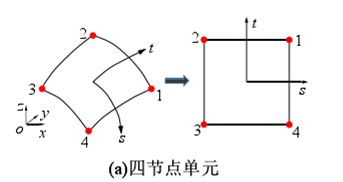
需求：给定空间平面\(S\)四个点的坐标\(Q_1(x,y,z),Q_2(x,y,z),Q_3(x,y,z),Q_4(x,y,z)\)，已知函数\(f(x,y,z)\)，求利用数值方法求解积分：\(\iint_Sf(x,y,z)\text dS\)。

解决方法：采用高斯-勒朗德积分方法进行求解。

---

计算步骤：

1. 转换坐标至参数坐标系，计算高斯点
2. 计算积分

坐标变换

\((x,y,z)\)与\((s,t,0)\)分别表示总体t坐标系与转换之后的参数坐标系，通过在单元内引入合适的形函数（又称插值函数）\(N_k(s, t)(k=1, 2,...,NE)\)并进行如下坐标变换：

\[\begin{align}(x,y,z)=\sum_{k=1}^{NE}N_k(s,t)(x_k,y_k,z_k) \quad s,t\in[-1,1]\end{align} \]

可以将物理空间\((x,y,z)\)的空间四边形单元转化为参数空间\((s,t,0)\)中的正方形单元，\(NE\)与\((x_k,y_k,z_k)\)分别代表单元节点数与第\(k\)个节点的坐标。在单元内，形函数\(N_k(s,t)\)应该满足以下两个条件：

\[\begin{align} N_k(s,t)&=\begin{cases} 1&在节点k上\\ 0&在其他节点上 \end{cases}\\ \sum_{k=1}^{NE}N_k(s,t)&=1 \end{align} \]

待定系数法，求解得到四节点形函数为

\[\begin{cases} N_1(s,t)=0.25(1+s)(1+t)\\ N_2(s,t)=0.25(1-s)(1+t)\\ N_3(s,t)=0.25(1-s)(1-t)\\ N_4(s,t)=0.25(1+s)(1-t) \end{cases}\\ \]

四节点等参单元的形函数是关于 $s, t \(的线性函数，而九节点等参单元的形函数是关于\) s, t $的二次函数。

积分坐标系转换

\[\begin{equation} \begin{aligned} \iint_{S_{}}f(x,y,z)\text dS(x,y,z)&=\iint_{S_{0}}f(s,t,0)|J(s,t)|\text dS(s,t,0)\\ &=\sum_{i=0}^{n}\sum_{j=0}^{n}A_iA_jf(s_i,t_j,0)|J(s_i,t_j)|\\ \end{aligned} \end{equation} \]

其中\(|J(s,t)|\)为\(Jacobi\)行列式

\[|J(s,t)|=\left| \frac{\boldsymbol r}{\partial s}\cross\frac{\boldsymbol r}{\partial t}\ \right | \]

式中\(\boldsymbol r=(x,y,z)\)与\(s,t\)的关系可以写作

\[\boldsymbol r=(x,y,z)=\sum_{k=1}^{NE}N_k(s,t)(x_k,y_k,z_k) \]

至此已经完成高斯勒朗德积分法的求解主要步骤。

另外，可将系数与函数值分离（避免多次计算高斯点），预先求解每个空间四边形面的高斯点位置与系数（系数与高斯点对应系数与坐标变换Jacobi系数矩阵相关）

测试实例

实例1

某二重积分

\[\int_{1.4}^{2}\int_{1}^{1.5} \text{ln}(x+2y)dydx\approx 0.42955453 \]

变换为区域\(R=\{(s,t)|-1\le s,t\le 1\}\)

\[s=\frac{1}{0.6}(2x-3.4),t=\frac{1}{0.5}(2y-2.5)\\ x=0.3s+1.7,y=0.25t+1.25 \]

\(n=2\)时的高斯积分节点与系数

\(i\)	0	1	2
\(s_i,t_i\)	\(-0.774596662\)	\(0\)	\(0.774596662\)
\(A_i\)	\(\frac{5}{9}\)	\(\frac{8}{9}\)	\(\frac{5}{9}\)

计算结果

%demo
clc;clear
Q=[1.4    1      0;
   2      1      0;
   2      1.5    0;
   1.4    1.5    0];

n=2;
[Gauss_P_A] = GetGaussPoint(Q,n);
P0=[0,0,3];
Func=@(Q) log(Q(1)+2*Q(2));
res=0;
for i=1:1:n*n
    res=res+Func(Gauss_P_A(i,1:3))*Gauss_P_A(i,4)*Gauss_P_A(i,5);
end
res

实例2

计算如下积分式：

clc;clear
Q=[0    0   0;
    1    0   0;
    1    1   0;
    0    1   0];
for n=1:1:4
    % n=2;
    [Gauss_P_A] = GetGaussPoint(Q,n);
    P0=[0,0,1];
    Func=@(Q) norm(Q-P0);
    res=0;
    for i=1:1:n*n
        res=res+Func(Gauss_P_A(i,1:3))*Gauss_P_A(i,4)*Gauss_P_A(i,5);
    end
    re(n)=res;
end

plot(1:1:n,re,'o');

n	积分数值
0	1.224744871391589
1	1.280924113061923
2	1.280797365089580
3	1.280788916595401

实例3

\[\frac{1}{r(P,Q)}=\frac{1}{\sqrt{(x_P-x_Q)^2+(y_P-y_Q)^2+(z_P-z_Q)^2}} \]

对\(P\)的全导数

\[\begin{align} \nabla{G(P,Q)}&=\nabla{\frac{1}{r(P,Q)}}\\&=-\frac{1}{r^3}(x_P-x_Q,y_P-y_Q,z_P-z_Q)\\&=-\frac{1}{r^3}(P-Q) \end{align} \]

GetGaussPoint.m

function [Gauss_P_A] = GetGaussPoint(Q,n)
%GETGAUSSPOINT 计算高斯点
%输入:Q面元点四个点(4*3),高斯点阶数n
%输出:Gauss_P_A:[高斯点位置,高斯点系数];
Nk1=@(s,t)0.25*(1+s)*(1+t);
Nk2=@(s,t)0.25*(1-s)*(1+t);
Nk3=@(s,t)0.25*(1-s)*(1-t);
Nk4=@(s,t)0.25*(1+s)*(1-t);

Nk1_s=@(s,t)0.25*( 1)*(1+t);
Nk2_s=@(s,t)0.25*(-1)*(1+t);
Nk3_s=@(s,t)0.25*(-1)*(1-t);
Nk4_s=@(s,t)0.25*( 1)*(1-t);

Nk1_t=@(s,t)0.25*(1+s)*( 1);
Nk2_t=@(s,t)0.25*(1-s)*( 1);
Nk3_t=@(s,t)0.25*(1-s)*(-1);
Nk4_t=@(s,t)0.25*(1+s)*(-1);

%高斯点对应系数
Gauss_Loc{1,1}=[+0,2];
Gauss_Loc{2,1}=[+0.577350300000000,1;
                -0.577350300000000,1];
Gauss_Loc{3,1}=[+0.774596700000000,0.555555600000000;
                -0,                0.888888900000000;
                -0.774596700000000,0.555555600000000];
Gauss_Loc{4,1}=[+0.861136300000000,0.347854800000000;
                +0.339981000000000,0.652145200000000;
                -0.339981000000000,0.652145200000000;
                -0.861136300000000,0.347854800000000];

The_Gauss=Gauss_Loc{n,1};
[Num,~]=size(The_Gauss);
Gauss_P_A=zeros(Num*Num,5);
count=1;
for i=1:1:Num
    for j=1:1:Num
        P_Loc=[The_Gauss(i,1),The_Gauss(j,1)];
        Gauss_P_A(count,1:3)=L2G(P_Loc);
        J=Jacobi(P_Loc);
        Gauss_P_A(count,4)=The_Gauss(i,2)*The_Gauss(j,2);
        %Jacobi系数
        Gauss_P_A(count,5)=J;
        count=count+1;
    end
end

    function Glo=L2G(Loc)
        Glo=Nk1(Loc(1),Loc(2))*Q(1,:)+...
            Nk2(Loc(1),Loc(2))*Q(2,:)+...
            Nk3(Loc(1),Loc(2))*Q(3,:)+...
            Nk4(Loc(1),Loc(2))*Q(4,:);
    end

    function J=Jacobi(Loc)
        s=Nk1_s(Loc(1),Loc(2))*Q(1,:)+...
            Nk2_s(Loc(1),Loc(2))*Q(2,:)+...
            Nk3_s(Loc(1),Loc(2))*Q(3,:)+...
            Nk4_s(Loc(1),Loc(2))*Q(4,:);
        t=Nk1_t(Loc(1),Loc(2))*Q(1,:)+...
            Nk2_t(Loc(1),Loc(2))*Q(2,:)+...
            Nk3_t(Loc(1),Loc(2))*Q(3,:)+...
            Nk4_t(Loc(1),Loc(2))*Q(4,:);
        J=norm(cross(s,t));
    end
end