人工智能基础复习3——知识与推理
07 Logical agents
一些建模范式
- 基于状态的模型:搜索问题,博弈
- 应用:路径搜索,玩游戏等
- 考虑状态、行动和代价
- 基于变量的模型:CSPs,贝叶斯网络
- 应用:调度、医疗诊断等
- 考虑状态和潜力
- 基于逻辑的模型: 命题逻辑、一阶逻辑
- 应用:定理证明、验证、推理
- 考虑逻辑公式和推理规则
- 基于状态的模型:搜索问题,博弈
- 应用:路径搜索,玩游戏等
- 考虑状态、行动和代价
- 基于变量的模型:CSPs,贝叶斯网络
- 应用:调度、医疗诊断等
- 考虑状态和潜力
- 基于逻辑的模型: 命题逻辑、一阶逻辑
- 应用:定理证明、验证、推理
- 考虑逻辑公式和推理规则
动机:聪明的个人助理
目录
- 逻辑智能体:基于知识的智能体
- 知识和推理的重要性
- 部分可观察的环境
- 自然语言理解
- 基于知识的智能体的灵活性
- 逻辑智能体:基于知识的智能体
- 知识和推理的重要性
- 部分可观察的环境
- 自然语言理解
- 基于知识的智能体的灵活性
逻辑的两个目标
- 代表世界的知识
- 推理知识
- 代表世界的知识
- 推理知识
Outline
- 基于知识的Agent
- Wumpus 世界
- 关于基于知识的智能体运转的例子
- 普遍的逻辑:逻辑和蕴涵
- 命题逻辑
- 等价、合法性和可满足性
- 推理规则与定理证明
- 前向链接
- 反向链接
- 归结
- 基于知识的Agent
- Wumpus 世界
- 关于基于知识的智能体运转的例子
- 普遍的逻辑:逻辑和蕴涵
- 命题逻辑
- 等价、合法性和可满足性
- 推理规则与定理证明
- 前向链接
- 反向链接
- 归结
知识库
- 知识库=形式语言中的句子集
- 将新语句添加到知识库——建立Agent(或其他系统)的声明方法:告诉(TELL)它需要知道什么
- 查询目前所知内容——它可以询问(ASK)自己需要做什么—答案应该从KB里面找
- Agents可以从知识层上观察,即它们知道什么而不管怎么实现的;或者在实现层,即KB中的数据结构和操纵它们的算法
一个简单的基于知识的Agent
- 知识库=形式语言中的句子集
- 将新语句添加到知识库——建立Agent(或其他系统)的声明方法:告诉(TELL)它需要知道什么
- 查询目前所知内容——它可以询问(ASK)自己需要做什么—答案应该从KB里面找
- Agents可以从知识层上观察,即它们知道什么而不管怎么实现的;或者在实现层,即KB中的数据结构和操纵它们的算法
一个简单的基于知识的Agent
function KB-AGENT(percept) returns an action
static: KB,a knowledge base
t,a counter,initially 0,indicating time
TELL(KB
- TELL->ASK->TELL
- 表示语言的细节隐含于MAKE-PERCEPT-SENTENCE和MAKE-ACTION-QUERY中
- 推理机制的细节隐藏于TELL和ASK中
- Agent必须能够:
- 表示状态和行为
- 加入新的感知信息
- 更新关于世界的状态表示
- 推导关于世界的隐藏信息
- 推导应采取的合适的行为
- 表示语言的细节隐含于MAKE-PERCEPT-SENTENCE和MAKE-ACTION-QUERY中
- 推理机制的细节隐藏于TELL和ASK中
- Agent必须能够:
- 表示状态和行为
- 加入新的感知信息
- 更新关于世界的状态表示
- 推导关于世界的隐藏信息
- 推导应采取的合适的行为
Wumpus世界的PEAS描述
- 性能度量:金子+100,死亡-1000,每一步-1,用箭-10
- 环境:4×4网格,智能体初始在[1,1],面向右方,金子和wumpus在[1,1]之外随机均匀分布,[1,1]之外的任意方格是陷阱的概率是0.2
- 执行器:左转,右转,前进,捡起,射箭
- 智能体可向前、左转或右转
- 智能体如果进入一个有陷阱或者活着的wumpus的方格,将死去。
- 如果智能体前方有一堵墙,那么向前移动无效
- Grab:捡起智能体所在方格中的一个物体
- Shoot:向智能体所正对方向射箭(只有一枝箭)
- 传感器:
- Smell:在wumpus所在之外以及与之直接相邻的方格内,智能体可以感知到臭气。
- Breeze:在与陷阱直接相邻的方格内,智能体可以感知到微风。
- Glitter(发光):在金子所处的方格内,智能体可以感知到闪闪金光。
- 当智能体撞到墙时,它感受到撞击。
- 当wumpus被杀死时,它发出洞穴内任何地方都可感知到的悲惨嚎叫。
- 以5个符号的列表形式将感知信息提供给智能体,例如(stench,breeze,none,none,none).
- 性能度量:金子+100,死亡-1000,每一步-1,用箭-10
- 环境:4×4网格,智能体初始在[1,1],面向右方,金子和wumpus在[1,1]之外随机均匀分布,[1,1]之外的任意方格是陷阱的概率是0.2
- 执行器:左转,右转,前进,捡起,射箭
- 智能体可向前、左转或右转
- 智能体如果进入一个有陷阱或者活着的wumpus的方格,将死去。
- 如果智能体前方有一堵墙,那么向前移动无效
- Grab:捡起智能体所在方格中的一个物体
- Shoot:向智能体所正对方向射箭(只有一枝箭)
- 传感器:
- Smell:在wumpus所在之外以及与之直接相邻的方格内,智能体可以感知到臭气。
- Breeze:在与陷阱直接相邻的方格内,智能体可以感知到微风。
- Glitter(发光):在金子所处的方格内,智能体可以感知到闪闪金光。
- 当智能体撞到墙时,它感受到撞击。
- 当wumpus被杀死时,它发出洞穴内任何地方都可感知到的悲惨嚎叫。
- 以5个符号的列表形式将感知信息提供给智能体,例如(stench,breeze,none,none,none).
Wumpus世界的表征
- 可观察的:不,只是部分感知
- 确定的:是的,结果完全确定
- 片段的:不,在行动水平上是连续的
- 静态的:是的,Wumpus和陷阱不移动
- 离散的:是的
- 单个Agent的:是的,Wumpus本质上是一种自然特征
探索wumpus世界
- 可观察的:不,只是部分感知
- 确定的:是的,结果完全确定
- 片段的:不,在行动水平上是连续的
- 静态的:是的,Wumpus和陷阱不移动
- 离散的:是的
- 单个Agent的:是的,Wumpus本质上是一种自然特征
探索wumpus世界
图略
普遍的逻辑
- 逻辑是一种形式语言,可以表示能得出结论的信息
- 语法(Syntax)定义了语言中的句子
- 语义(Semantics)定义了句子的意思,即语义定义了每个语句关于每个可能世界的真值
蕴涵
- 蕴涵意为一个语句逻辑上跟随另一个语句而出现:KB |=α
- 知识库KB蕴涵句子α当且仅当在KB为真的每个世界中,α也为真
- 蕴涵是句子间的关系,其基于语义
Models模型
- 当需要精确描述时,用术语模型取代“可能世界”
- “m是α的一个模型”表示语句α在模型m中为真
- M(α)是α的所有模型的集合,则KB|=α当且仅当M(KB)∈M(α),在KB为真的所有模型中α为真
wumpus世界中的蕴含
- 考虑相邻的方格是否包含陷阱
- KB = wumpus-world rules + observations
- α1 = “[1,2]安全“,KB|=α1,通过模型检验证明
- 在KB为真的每个模型中,α1也为真,因此KB|=α1
- α2 = “[2,2]安全“,KB≠α2
- 在KB为真的某些模型中,α为假,因此KB≠α2
- 逻辑是一种形式语言,可以表示能得出结论的信息
- 语法(Syntax)定义了语言中的句子
- 语义(Semantics)定义了句子的意思,即语义定义了每个语句关于每个可能世界的真值
蕴涵
- 蕴涵意为一个语句逻辑上跟随另一个语句而出现:KB |=α
- 知识库KB蕴涵句子α当且仅当在KB为真的每个世界中,α也为真
- 蕴涵是句子间的关系,其基于语义
Models模型
- 当需要精确描述时,用术语模型取代“可能世界”
- “m是α的一个模型”表示语句α在模型m中为真
- M(α)是α的所有模型的集合,则KB|=α当且仅当M(KB)∈M(α),在KB为真的所有模型中α为真
wumpus世界中的蕴含
- 考虑相邻的方格是否包含陷阱
- KB = wumpus-world rules + observations
- α1 = “[1,2]安全“,KB|=α1,通过模型检验证明
- 在KB为真的每个模型中,α1也为真,因此KB|=α1
- α2 = “[2,2]安全“,KB≠α2
- 在KB为真的某些模型中,α为假,因此KB≠α2
Inference推理
- 如果推理算法i可以根据KB导出α,我们表示为:KB|-iα,读为“i从KB导出α“
- KB的所有推论集合是一个干草堆,α是针,蕴含=干草堆里的针,推理=找到它
- 可靠性——只导出语义蕴涵句:i是可靠的,若对任意KB|-iα真,则KB|-α也真
- 完备性——可以生成任一蕴涵句:i是完备的,如果对任意KB|-α,则KB|-iα也真
命题逻辑:Syntax语法
- 命题逻辑是最简单的逻辑——阐明基本思想
- 原子语句:命题符号P1,P2等是句子,代表一个或为真或为假的命题
- 复合句:
- 如果S是一个句子,则┐S也是一个句子(negation非,否定式)
- 如果S1和S2是句子,则S1∧S2是句子(conjunction与,合取式)
- 如果S1和S2是句子,则S1∨S2是句子(disjunction或,析取式)
- 如果S1和S2是句子,则S1=>S2是句子(implication蕴涵,蕴涵式)
- 如果S1和S2是句子,则S1<=>S2是句子(biconditional当且仅当,双向蕴涵式)
- 如果推理算法i可以根据KB导出α,我们表示为:KB|-iα,读为“i从KB导出α“
- KB的所有推论集合是一个干草堆,α是针,蕴含=干草堆里的针,推理=找到它
- 可靠性——只导出语义蕴涵句:i是可靠的,若对任意KB|-iα真,则KB|-α也真
- 完备性——可以生成任一蕴涵句:i是完备的,如果对任意KB|-α,则KB|-iα也真
命题逻辑:Syntax语法
- 命题逻辑是最简单的逻辑——阐明基本思想
- 原子语句:命题符号P1,P2等是句子,代表一个或为真或为假的命题
- 复合句:
- 如果S是一个句子,则┐S也是一个句子(negation非,否定式)
- 如果S1和S2是句子,则S1∧S2是句子(conjunction与,合取式)
- 如果S1和S2是句子,则S1∨S2是句子(disjunction或,析取式)
- 如果S1和S2是句子,则S1=>S2是句子(implication蕴涵,蕴涵式)
- 如果S1和S2是句子,则S1<=>S2是句子(biconditional当且仅当,双向蕴涵式)
命题逻辑:Semantics语义
- 模型简单的固定了每个命题符号的真值
- 5种逻辑连接符的真值表
Wumpus世界的句子
- 如果[i,j]有陷阱则Pi,j是真,如果[i,j]有微风则Bi,j是真,陷阱导致相邻方格的微风。
- B1,1<=>(P1,2vP2,1)
- B2,1<=>(P1,1vP2,2vP3,1)
- 一个方格有微风当且仅当相邻方格有陷阱
通过枚举推理
- 对于所有模型的深度优先枚举是可靠的和完备的
- 模型简单的固定了每个命题符号的真值
- 5种逻辑连接符的真值表
Wumpus世界的句子
- 如果[i,j]有陷阱则Pi,j是真,如果[i,j]有微风则Bi,j是真,陷阱导致相邻方格的微风。
- B1,1<=>(P1,2vP2,1)
- B2,1<=>(P1,1vP2,2vP3,1)
- 一个方格有微风当且仅当相邻方格有陷阱
通过枚举推理
- 对于所有模型的深度优先枚举是可靠的和完备的
function TT-ENTAILS?(KB,a) returns true or false
inputs:KB,the knowledge base,a sentence in propositional logic a,the query,a sentence in propositional logic
symbols←a list of the proposition symbols in KB and a
return TT-CHECK-ALL(KB,a,symbols,[])
function TT-CHECK-ALL(KB,a,symbols,model) returns true or false
if EMPTY?(symbols)then
if PL-TRUE?(KB,model)then return PL-TRUE?(a,model)
else return true
else do
P←FIRST(symbols);rest←REST(symbols)
return TT-CHECK-ALL(KB,a,restEXTEND(P,true,model)) and TT-CHECK-ALL(KB,a,rest,EXTEND(P,false,model))
逻辑等价
- 两个句子是逻辑等价的:α=β 当且仅当α|=β and β|=α
- ∧的可交换性、结合律,∨的可交换性、结合律,双重否定消去,逆否命题,蕴涵消去,双向蕴涵消去,摩根律,摩根律,∧对∨的分配率,∨对∧的分配率
合法性与可满足性
- 一个句子是合法的如果对于所有的模型,它都是真值
- 合法性通过演绎定理与推理联系:KB|=α 当且仅当(KB|=α)是合法的
- 一个句子是可满足的如果对于部分模型它是真值
- 一个句子是不可满足的如果它在任何模型中都不为真
- 可满足性根据下列规则与推理联系:KB|=α当且仅当(KB∧┐α)是不可满足的,即通过归谬,反证法来证明α:假定α为假,并证明这将推导出和已知公理KB的一个矛盾
证明方法
- 证明方法分为两种:
- 推理规则的应用:
- 从旧的句子中产生新的合法的(可靠的)句子,证明=推理规则的应用序列,寻找证明的过程与搜索问题中寻找解的过程非常类似:定义后继函数以便生成推理规则所有可能的应用。
- 通常需要将句子转换成范式
- 模型检查:
- 枚举真值表
- 改进的回溯
- 模型空间中的启发式搜索(可靠但不完备)
前向链接和反向链接
- 两个句子是逻辑等价的:α=β 当且仅当α|=β and β|=α
- ∧的可交换性、结合律,∨的可交换性、结合律,双重否定消去,逆否命题,蕴涵消去,双向蕴涵消去,摩根律,摩根律,∧对∨的分配率,∨对∧的分配率
合法性与可满足性
- 一个句子是合法的如果对于所有的模型,它都是真值
- 合法性通过演绎定理与推理联系:KB|=α 当且仅当(KB|=α)是合法的
- 一个句子是可满足的如果对于部分模型它是真值
- 一个句子是不可满足的如果它在任何模型中都不为真
- 可满足性根据下列规则与推理联系:KB|=α当且仅当(KB∧┐α)是不可满足的,即通过归谬,反证法来证明α:假定α为假,并证明这将推导出和已知公理KB的一个矛盾
证明方法
- 证明方法分为两种:
- 推理规则的应用:
- 从旧的句子中产生新的合法的(可靠的)句子,证明=推理规则的应用序列,寻找证明的过程与搜索问题中寻找解的过程非常类似:定义后继函数以便生成推理规则所有可能的应用。
- 通常需要将句子转换成范式
- 模型检查:
- 枚举真值表
- 改进的回溯
- 模型空间中的启发式搜索(可靠但不完备)
- 霍恩形式(限定)
- KB = conjunction (与) of Horn clauses 霍恩子句
- 霍恩子句= 命题符号,或符号连接=>符号
- 分离规则,肯定前件的假言推理:
- 对于霍恩KBs来说是完备的
前向链接
- 从知识库中的已知事实(正文字)开始。如果蕴涵的所有前提已知,那么把它的结论加到已知事实集。持续这一过程,直到询问q被添加或者直到无法进行更进一步的推理
- 算法:
function PL-FC-ENTAILS?(KB,q)returns true or false
inputs:KB,the knowledge base,a set of propositional Horn clauses q,the query,aproposition symbol
local variables:count,a table,indexed by clause,initially the number of premises inferred,a table, indexed by symbol,each entry initially false agenda,a list of symbols,initially the symbols known in KB
while agenda is not empty do
p←POP(agenda)
unless inferred[p] do
inferred[p]←true
for each Horn clause c in whose premise p appears do
decrement count[c]
if count[c] = 0 then do
if HEAD[c]=q then return true
PUSH(HEAD[c],agenda)
return false
性质:
- 对于Horn KB,前向链接是
- 可靠的:每个推理本质上是分离规则的一个应用
- 完备的:每个被蕴涵的原子语句都将得以生成
完备性证明
FC可推出每个被KB蕴涵的原子语句
1. FC到达不动点以后,不可能再出现新的推理。
2. 考察inferred表的最终状态,参与推理过程的每个符号为true,其他为false。把该推理表看做一个逻辑模型m
3. 原始KB中的每个确定子句在该模型m中都为真
证明:假设某个子句a1∧...∧ak=>b 在m中为false,那么 a1∧...∧ak 在m中为true,b在m中为false,与算法已经到达一个不动点相矛盾。
4. m是KB的一个模型
5. 如果KB|=q,q在KB的所有模型中必须为真,包括m
6. q在m中为真->在inferred表中为真->被FC算法推断出来
后向链接
- 从查询q反向进行:
- 通过BC证明q,检查是否q已知为真,寻找知识库中那些以q为结论的蕴涵,证明其中一个蕴涵的所有前提为真
- 避免循环:检查是否有新的目标已经在目标栈上
- 避免重复工作:检查是否有新的目标
- 已经被证明为真,或者
- 已经失败
后向链接图略。
- 对于Horn KB,前向链接是
- 可靠的:每个推理本质上是分离规则的一个应用
- 完备的:每个被蕴涵的原子语句都将得以生成
完备性证明
FC可推出每个被KB蕴涵的原子语句
1. FC到达不动点以后,不可能再出现新的推理。
2. 考察inferred表的最终状态,参与推理过程的每个符号为true,其他为false。把该推理表看做一个逻辑模型m
3. 原始KB中的每个确定子句在该模型m中都为真
证明:假设某个子句a1∧...∧ak=>b 在m中为false,那么 a1∧...∧ak 在m中为true,b在m中为false,与算法已经到达一个不动点相矛盾。
4. m是KB的一个模型
5. 如果KB|=q,q在KB的所有模型中必须为真,包括m
6. q在m中为真->在inferred表中为真->被FC算法推断出来
后向链接
- 从查询q反向进行:
- 通过BC证明q,检查是否q已知为真,寻找知识库中那些以q为结论的蕴涵,证明其中一个蕴涵的所有前提为真
- 避免循环:检查是否有新的目标已经在目标栈上
- 避免重复工作:检查是否有新的目标
- 已经被证明为真,或者
- 已经失败
后向链接图略。
前向 vs. 后向链接
- FC是数据驱动的,自动化,无意识处理,如物体识别,路径决策;可能会进行许多和目标不相关的工作
- BC是目标指导的,适合问题求解,如:我的钥匙在哪里?我怎么进展PHD项目?
- BC的复杂度可以远远小于KB大小的线性
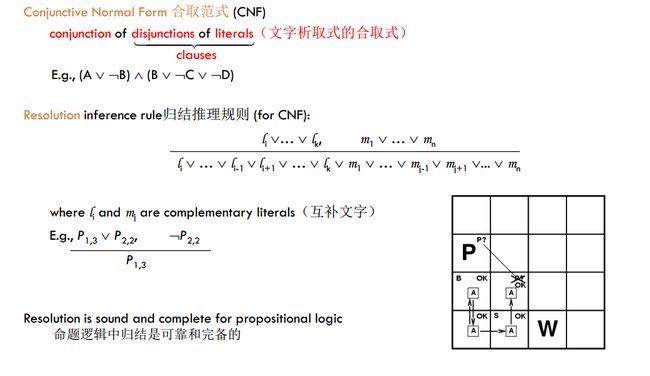
Resolution归结
- 合取范式(CNF):文字析取式的合取式
- 归结推理规则(for CNF):
- CNF的转换
- 归结算法
- 回忆:KB操作归结为可满足性,KB|=α当且仅当(KB∧┐α)是不可满足的
- 算法:基于归结的推理
- 转换所有式子为CNF
- 重复使用归结规则
- 如果推导失败,返回不可满足性
- 反证法,即证明KB∧α不可满足:

- FC是数据驱动的,自动化,无意识处理,如物体识别,路径决策;可能会进行许多和目标不相关的工作
- BC是目标指导的,适合问题求解,如:我的钥匙在哪里?我怎么进展PHD项目?
- BC的复杂度可以远远小于KB大小的线性
Resolution归结
- 合取范式(CNF):文字析取式的合取式
- 归结推理规则(for CNF):

- CNF的转换
- 归结算法
- 回忆:KB操作归结为可满足性,KB|=α当且仅当(KB∧┐α)是不可满足的
- 算法:基于归结的推理
- 转换所有式子为CNF
- 重复使用归结规则
- 如果推导失败,返回不可满足性
- 反证法,即证明KB∧α不可满足:
function PL-RESOLUTION(KB,a)returns true or false
inputs:KB,the knowledge base,a sentence in propositional logic a,the query,a sentence in propositional logic
clauses←the set of clauses in the CNF representation of KB∧┐a
new←{}
loop do
for each Ci,Cj in clauses do
resolvents←PL-RESOLVE(Ci,Cj)
if resolvents contains the empty clause then return true
new←new∪resolvents
if new∈clauses then return false
clauses←clauses∪new
比较
- Horn子句 任何子句
- 演绎推理 归结
- 线性时间 指数时间
- 少的表现 更多表现
总结
- 逻辑Agents将推理应用到知识库中,以获得新的信息和作出决定
- 逻辑的基本概念:
- 语法:命题的形式结构
- 语义:句子模型的真值
- 蕴涵:给定一个命题,则另一个命题为真
- 推理:从一个命题推出另一个命题
- 可靠性:派生只产生蕴涵句
- 完备性:派生可以产生所有蕴涵句
- Wumpus世界需要代表部分的能力和否定的信息,原因的情况下等……
- 前向、后向链接是线性时间的,对Horn子句是完备的,对命题逻辑的推理是完备的
- 命题逻辑缺乏表现力
- 逻辑Agents将推理应用于知识库来推导新的信息及作出决策
- 基本的逻辑概念:
- 语法:命题的形式结构
- 语义:命题wrt模型的真值
- 蕴涵:给定一个命题,另一个命题为真
- 推理:从一个命题推导出另一个命题
- 可靠性:只推理出蕴涵命题
- 完备性:推理出所有的蕴涵命题
- 前向、后向链接对于Horn子句是线性时间的、完备的,对于命题逻辑的归结是完备的
- 命题逻辑缺乏表现力
- Horn子句 任何子句
- 演绎推理 归结
- 线性时间 指数时间
- 少的表现 更多表现
总结
- 逻辑Agents将推理应用到知识库中,以获得新的信息和作出决定
- 逻辑的基本概念:
- 语法:命题的形式结构
- 语义:句子模型的真值
- 蕴涵:给定一个命题,则另一个命题为真
- 推理:从一个命题推出另一个命题
- 可靠性:派生只产生蕴涵句
- 完备性:派生可以产生所有蕴涵句
- Wumpus世界需要代表部分的能力和否定的信息,原因的情况下等……
- 前向、后向链接是线性时间的,对Horn子句是完备的,对命题逻辑的推理是完备的
- 命题逻辑缺乏表现力
08 First order logic
Last chapter- 逻辑Agents将推理应用于知识库来推导新的信息及作出决策
- 基本的逻辑概念:
- 语法:命题的形式结构
- 语义:命题wrt模型的真值
- 蕴涵:给定一个命题,另一个命题为真
- 推理:从一个命题推导出另一个命题
- 可靠性:只推理出蕴涵命题
- 完备性:推理出所有的蕴涵命题
- 前向、后向链接对于Horn子句是线性时间的、完备的,对于命题逻辑的归结是完备的
- 命题逻辑缺乏表现力
Outline
- 为什么 FOL
- FOL的语法和语义
- 使用FOL
- FOL的知识工程
- FOL的语法和语义
- 使用FOL
- FOL的知识工程
命题逻辑的优点
- 命题逻辑是陈述性的
- 知识和推理分开,而且推理完全不依赖于领域
- 对比:程序设计语言——过程性语言
- 缺乏从其他事实派生出事实的通用机制
- 对数据结构的更新通过一个领域特定的过程来完成
- 命题逻辑允许不完全、分离的、否定的信息(不像大多数数据结构和数据库)
- 命题逻辑是合成性的:
- 语句的含义是它的各部分含义的一个函数
- 命题逻辑的含义是独立于内容的
- 不像自然语言,含义依赖于内容
命题逻辑的缺点
- 命题逻辑有非常有限的表达能力
- 不像自然语言
- 不能表达“陷阱导致相邻方格的微风”,只能使用B1,1<=>(P1,2 V P2,1)
- 对象和关系:命题拥有更多的内部结构
- 量词和变词:所有的量词都适用于每个人,不想把它们全部列举出来
一阶逻辑
- 采用命题逻辑的基础——陈述式、上下文无关和合成语义,并借用自然语言的思想
- 命题逻辑假设世界包含事实,而一阶逻辑(类似于自然语言)假设世界包含:
- 对象:人,房子,数字,颜色,棒球赛,战争等
- 关系:红色,圆的,质数等
- 函数:比……更,加上等
- 谓词用来描述个体(可以独立存在的事物)之间的关系或属性
逻辑综合
- 命题逻辑是陈述性的
- 知识和推理分开,而且推理完全不依赖于领域
- 对比:程序设计语言——过程性语言
- 缺乏从其他事实派生出事实的通用机制
- 对数据结构的更新通过一个领域特定的过程来完成
- 命题逻辑允许不完全、分离的、否定的信息(不像大多数数据结构和数据库)
- 命题逻辑是合成性的:
- 语句的含义是它的各部分含义的一个函数
- 命题逻辑的含义是独立于内容的
- 不像自然语言,含义依赖于内容
命题逻辑的缺点
- 命题逻辑有非常有限的表达能力
- 不像自然语言
- 不能表达“陷阱导致相邻方格的微风”,只能使用B1,1<=>(P1,2 V P2,1)
- 对象和关系:命题拥有更多的内部结构
- 量词和变词:所有的量词都适用于每个人,不想把它们全部列举出来
一阶逻辑
- 采用命题逻辑的基础——陈述式、上下文无关和合成语义,并借用自然语言的思想
- 命题逻辑假设世界包含事实,而一阶逻辑(类似于自然语言)假设世界包含:
- 对象:人,房子,数字,颜色,棒球赛,战争等
- 关系:红色,圆的,质数等
- 函数:比……更,加上等
- 谓词用来描述个体(可以独立存在的事物)之间的关系或属性
逻辑综合
语言 本体论约定(世界中存在的) 认识论约定(智能体对事实所相信的内容)
命题逻辑 事实 真/假/未知
一阶逻辑 事实、对象、关系 真/假/未知
时序逻辑 事实、对象、关系、时间 真/假/未知
概率逻辑 事实 信度∈[0,1]
命题逻辑 事实 真/假/未知
一阶逻辑 事实、对象、关系 真/假/未知
时序逻辑 事实、对象、关系、时间 真/假/未知
概率逻辑 事实 信度∈[0,1]
一阶逻辑的模型:Example
FOL的语法:基本元素
- 常量:KingJohn,2,USTC,...
- 谓词:Brother,>,...
- 函数:Sqrt,LeftLegOf,...
- 连接词:┐,=>,∧,∨,<=>
- 等词: =
- 量词:∀,∃
FOL的语法:基本元素
- 常量:KingJohn,2,USTC,...
- 谓词:Brother,>,...
- 函数:Sqrt,LeftLegOf,...
- 连接词:┐,=>,∧,∨,<=>
- 等词: =
- 量词:∀,∃
原子语句
- 项 = function(term1,...,termn) 或常量或变量
- 原子语句 = Predicate(term1,...,termn) 或 term1=term2
- 项 = function(term1,...,termn) 或常量或变量
- 原子语句 = Predicate(term1,...,termn) 或 term1=term2
复合语句
- 复合语句是由原子语句用连接词构成的
¬S, S1 ∧ S2, S1 ∨ S2, S1 ⇒ S2, S1 ⇔ S2
- E.g. Sibling(KingJohn,Richard) ⇒ Sibling(Richard,KingJohn)
>(1,2) ∨ ≤ (1,2)
>(1,2) ∧ ¬ >(1,2)
- 复合语句是由原子语句用连接词构成的
¬S, S1 ∧ S2, S1 ∨ S2, S1 ⇒ S2, S1 ⇔ S2
- E.g. Sibling(KingJohn,Richard) ⇒ Sibling(Richard,KingJohn)
>(1,2) ∨ ≤ (1,2)
>(1,2) ∧ ¬ >(1,2)
一阶逻辑的真值
- 语句的真值由一个模型和对句子符号的解释来判定
- 模型包含对象(域元素)和他们之间的关系
- 我们需要一个对分别被常量、谓词和函数符号指代的对象、关系和函数进行详细说明的解释
- 解释指定的指代
- 常量符号 → 对象
- 谓词符号 → 关系
- 函数符号 → 函数关系
- 一个原子语句谓词(term1,...,termn)为真,当且仅当被term1,...,termn指代的对象在被谓词指代的关系中。
- 语句的真值由一个模型和对句子符号的解释来判定
- 模型包含对象(域元素)和他们之间的关系
- 我们需要一个对分别被常量、谓词和函数符号指代的对象、关系和函数进行详细说明的解释
- 解释指定的指代
- 常量符号 → 对象
- 谓词符号 → 关系
- 函数符号 → 函数关系
- 一个原子语句谓词(term1,...,termn)为真,当且仅当被term1,...,termn指代的对象在被谓词指代的关系中。
真值例子
- 考虑以下解释
- Richard → Richard the Lionheart
- John → the evil King John
- Brother → the brotherhood relation
- 根据这一解释,Brother(Richard, John)为真仅当Richard the Lionheart和the evil King John在模型中是兄弟关系
- 考虑以下解释
- Richard → Richard the Lionheart
- John → the evil King John
- Brother → the brotherhood relation
- 根据这一解释,Brother(Richard, John)为真仅当Richard the Lionheart和the evil King John在模型中是兄弟关系
FOL的模型:Lots!
- 命题逻辑中的蕴涵可以通过枚举模型来计算
- 我们可以根据给定的KB词汇表,枚举FOL模型:
- 命题逻辑中的蕴涵可以通过枚举模型来计算
- 我们可以根据给定的KB词汇表,枚举FOL模型:
For each number of domain elements n from 1 to limit
For each k-ary predicate Pk in the vocabulary
For each possible k-ary relation on n objects
For each constant symbok C in the vocabulary
For each choice of referent for C from n objects...
全称量词
- ∀ “对于所有的……”
- Everyone at USTC is smart: ∀ x At(x,USTC) => Smart(x)
- ∀
- Everyone at USTC is smart: ∀ x At(x,USTC) => Smart(x)
常见的错误
- 通常,=>主要与∀连接,在需要用全称量词书写一般规则的时候,=>的真值表项是一个理想的选择
- 常见错误:使用∧作为∀的主要连接词
存在量词
- ∃ “存在一个……,这样以致“ 或 “对于某个……”
- 通常,∧是∃的主要连接词
- 常见错误,使用=>作为∃的主要连接词
- 通常,=>主要与∀连接,在需要用全称量词书写一般规则的时候,=>的真值表项是一个理想的选择
- 常见错误:使用∧作为∀的主要连接词
存在量词
- ∃
- 通常,∧是∃的主要连接词
- 常见错误,使用=>作为∃的主要连接词
量词的性质
- ∀ x ∀ y = ∀ y ∀ x
- ∃ x ∃ y = ∃ y ∃ x
-∃ x ∀ y ≠ ∀ y ∃ x
- 量词的二义性
- ∀x Likes(x,IceCream) ¬∃x ¬Likes(x,IceCream)
- ∃x Likes(x,Broccoli) ¬∀x ¬Likes(x,Broccoli)
等式
- term1=term2当且仅当term1和term2指代的对象是相同的
- 亲兄弟定义:
∀x,y Sibling(x,y) ⇔ [¬(x = y) ∧ ∃m,f ¬ (m = f) ∧ Parent(m,x)
∧ Parent(f,x) ∧ Parent(m,y) ∧ Parent(f,y)]
- ∀ x ∀ y = ∀ y ∀ x
- ∃ x ∃ y = ∃ y ∃ x
-∃ x ∀ y ≠ ∀ y ∃ x
- 量词的二义性
- ∀x Likes(x,IceCream) ¬∃x ¬Likes(x,IceCream)
- ∃x Likes(x,Broccoli) ¬∀x ¬Likes(x,Broccoli)
等式
- term1=term2当且仅当term1和term2指代的对象是相同的
- 亲兄弟定义:
∀x,y Sibling(x,y) ⇔ [¬(x = y) ∧ ∃m,f ¬ (m = f) ∧ Parent(m,x)
∧ Parent(f,x) ∧ Parent(m,y) ∧ Parent(f,y)]
使用FOL
- 亲属关系领域:
- ∀ x, y Brother(x,y) ⇒ Sibling(x, y)
- ∀ x, y Sibling(x, y) ⇔ Sibling(y, x).
- ∀ x, y Mother(x, y) ⇔ (Female(x) ∧ Parent(x, y))
- ∀ x, y Cousin(x,y) ⇔ ∃ p, ps Parent(p, x) ∧ Sibling(ps, p) ∧Parent(ps, y)
- 集合领域:
- 集合就是空集或通过将一些元素添加到一个集合而构成:∀s Set(s) ⇔ (s = {} ) ∨ (∃x,s2 Set(s2) ∧ s = {x|s2})
- 空集没有任何元素,也就是说,空集无法再分解为更小的集合和元素:¬∃x,s {x|s} = {}
- 将已经存在于集合中的元素添加到该集合,无任何变化:∀x,s x ∈ s ⇔ s = {x|s}
- 集合的元素仅是那些被添加到集合中的元素:∀x,s x ∈ s ⇔ [ ∃y,s2 (s = {y|s2} ∧ (x = y ∨ x ∈ s2))]
- 一个集合是另一个集合的子集,当且仅当第一个集合的所有元素都是第二个集合的元素:∀s1,s2 s1 ⊆ s2 ⇔ (∀x x ∈ s1 ⇒ x ∈ s2)
- 两个集合是相同的,当且仅当它们互为子集:∀s1,s2 (s1 = s2) ⇔ (s1 ⊆ s2 ∧ s2 ⊆ s1)
- 一个对象是两个集合的交集的元素,当且仅当它同时是这两个集合的元素:∀x,s1,s2 x ∈ (s1 ∩ s2) ⇔ (x ∈ s1 ∧ x ∈ s2)
- 一个对象是两个集合的并集的元素,当且仅当它是其中某一集合的元素:∀x,s1,s2 x ∈ (s1 ∪ s2) ⇔ (x ∈ s1 ∨ x ∈ s2)
- 亲属关系领域:
- ∀ x, y Brother(x,y) ⇒ Sibling(x, y)
- ∀ x, y Sibling(x, y) ⇔ Sibling(y, x).
- ∀ x, y Mother(x, y) ⇔ (Female(x) ∧ Parent(x, y))
- ∀ x, y Cousin(x,y) ⇔ ∃ p, ps Parent(p, x) ∧ Sibling(ps, p) ∧Parent(ps, y)
- 集合领域:
- 集合就是空集或通过将一些元素添加到一个集合而构成:∀s Set(s) ⇔ (s = {} ) ∨ (∃x,s2 Set(s2) ∧ s = {x|s2})
- 空集没有任何元素,也就是说,空集无法再分解为更小的集合和元素:¬∃x,s {x|s} = {}
- 将已经存在于集合中的元素添加到该集合,无任何变化:∀x,s x ∈ s ⇔ s = {x|s}
- 集合的元素仅是那些被添加到集合中的元素:∀x,s x ∈ s ⇔ [ ∃y,s2 (s = {y|s2} ∧ (x = y ∨ x ∈ s2))]
- 一个集合是另一个集合的子集,当且仅当第一个集合的所有元素都是第二个集合的元素:∀s1,s2 s1 ⊆ s2 ⇔ (∀x x ∈ s1 ⇒ x ∈ s2)
- 两个集合是相同的,当且仅当它们互为子集:∀s1,s2 (s1 = s2) ⇔ (s1 ⊆ s2 ∧ s2 ⊆ s1)
- 一个对象是两个集合的交集的元素,当且仅当它同时是这两个集合的元素:∀x,s1,s2 x ∈ (s1 ∩ s2) ⇔ (x ∈ s1 ∧ x ∈ s2)
- 一个对象是两个集合的并集的元素,当且仅当它是其中某一集合的元素:∀x,s1,s2 x ∈ (s1 ∪ s2) ⇔ (x ∈ s1 ∨ x ∈ s2)
和FOL KBs进行互动
- 假设一个wumpus-world agent使用FOL KB并且在t=5感觉到气味和微风:
- Tell(KB,Percept([Smell,Breeze,None],5))
- Ask(KB,∃a BestAction(a,5))
- 绑定表
wumpus世界的知识库
- 感知:∀t,s,b Percept([s,b,Glitter],t) ⇒ Glitter(t)
- 反射: ∀t Glitter(t) ⇒ BestAction(Grab,t)
- 内部状态反射:∀ t AtGold(t) ∧ ¬ Holding(Gold, t) ⇒ BestAction(Grab, t)
- 假设一个wumpus-world agent使用FOL KB并且在t=5感觉到气味和微风:
- Tell(KB,Percept([Smell,Breeze,None],5))
- Ask(KB,∃a BestAction(a,5))
- 绑定表
wumpus世界的知识库
- 感知:∀t,s,b Percept([s,b,Glitter],t) ⇒ Glitter(t)
- 反射: ∀t Glitter(t) ⇒ BestAction(Grab,t)
- 内部状态反射:∀ t AtGold(t) ∧ ¬ Holding(Gold, t) ⇒ BestAction(Grab, t)
演绎隐藏属性
- 邻接方格定义:∀x,y,a,b Adjacent([x,y],[a,b]) ⇔ [a,b] ∈ {[x+1,y], [x-1,y],[x,y+1],[x,y-1]}
- 方格定义:∀s,t At(Agent,s,t) ∧ Breeze(t) ⇒ Breezy(s)
- 陷阱邻近的方格被闻到:
- 诊断规则:从结果推导原因:∀s Breezy(s) ⇒ ∃r Adjacent(r,s) ∧ Pit(r)
- 因果规则:从原因推导结果:∀r,s Adjacent(r,s)∧Pit(r) ⇒ Breezy(s)
- 均不是完备的——因果规则没有告诉我们远离陷阱的方格是否可以闻
- Breezy谓词的定义:∀s Breezy(s) ⇔ ∃r Adjacent(r,s) ∧ Pit(r)
- 邻接方格定义:∀x,y,a,b Adjacent([x,y],[a,b]) ⇔ [a,b] ∈ {[x+1,y], [x-1,y],[x,y+1],[x,y-1]}
- 方格定义:∀s,t At(Agent,s,t) ∧ Breeze(t) ⇒ Breezy(s)
- 陷阱邻近的方格被闻到:
- 诊断规则:从结果推导原因:∀s Breezy(s) ⇒ ∃r Adjacent(r,s) ∧ Pit(r)
- 因果规则:从原因推导结果:∀r,s Adjacent(r,s)∧Pit(r) ⇒ Breezy(s)
- 均不是完备的——因果规则没有告诉我们远离陷阱的方格是否可以闻
- Breezy谓词的定义:∀s Breezy(s) ⇔ ∃r Adjacent(r,s) ∧ Pit(r)
FOL中的知识工程
1. 确定任务
2. 搜集相关知识
3. 确定谓词、函数和常量的词汇表
4. 对域的通用知识进行编码
5. 对特定问题实例的描述进行编码
6. 把查询提交给推理过程并获取答案
7. 调试知识库
电路领域
- 一位全加器:最初的两个输入是需要相加的两位,第三个输入是一个进位。第一个输出是和,第二个输出是下一个加法器的进位。
1. 确定任务:电路是否相加正确(电路确定)
2. 搜集相关知识:导线和门的组成,门的类型(AND,OR,XOR,NOT),不相关:尺寸、形状、颜色、门的成本
3. 确定词汇表:Type(X1) = XOR, Type(X1,XOR) XOR(X1)
4. 对域的通用知识进行编码
(1). 如果两个接线端是相连的,那么它们具有相同的信号:∀t1,t2 Connected(t1, t2) ⇒ Signal(t1) = Signal(t2)
(2) 每个接线端的信号不是1就是0(不可能两者都是):∀t Signal(t) = 1 ∨ Signal(t) = 0 1 ≠ 0
(3)Connected是一个可交换谓词:∀t1,t2 Connected(t1, t2) ⇒ Connected(t2, t1)
(4)或门的输出为1,当且仅当它的某一个输入为1:∀g Type(g) = OR ⇒ Signal(Out(1,g)) = 1 ⇔ ∃n Signal(In(n,g)) = 1
(5)与门的输出为0,当且仅当它的某一个输入为0:∀g Type(g) = AND ⇒ Signal(Out(1,g)) = 0 ⇔ ∃n Signal(In(n,g)) = 0
(6)异或门的输出为1,当且仅当它的输入是不相同的:∀g Type(g) = XOR ⇒ Signal(Out(1,g)) = 1 ⇔ Signal(In(1,g)) ≠ Signal(In(2,g))
(7)非门的输出与它的输入相反:∀g Type(g) = NOT ⇒ Signal(Out(1,g)) ≠ Signal(In(1,g))
5. 对特定问题实例的描述进行编码
- 首先对门加以分类:Type(X1)=XOR Type(X2)=XOR Type(A1)=AND Type(A2)=AND Type(O1)=OR
- 其次说明门与门之间的连接
Connected(Out(1,X1),In(1,X2)) Connected(In(1,C1),In(1,X1))
Connected(Out(1,X1),In(2,A2)) Connected(In(1,C1),In(1,A1))
Connected(Out(1,A2),In(1,O1)) Connected(In(2,C1),In(2,X1))
Connected(Out(1,A1),In(2,O1)) Connected(In(2,C1),In(2,A1))
Connected(Out(1,X2),Out(1,C1)) Connected(In(3,C1),In(2,X2))
Connected(Out(1,O1),Out(2,C1)) Connected(In(3,C1),In(1,A2))
6. 把查询提交给推理过程并获取答案
- 对于1位全加器有哪些可能的输入与输出组合?
- ∃i1,i2,i3,o1,o2 Signal(In(1, C1)) = i1 ∧Signal(In(2,C1)) = i2 ∧ Signal(In(3,C1)) = i3 ∧Signal(Out(1,C1)) = o1 ∧ Signal(Out(2,C1)) = o2
7. 调试知识库
- 可能省略了断言 1 ≠ 0
- 对异或门(XOR)尤其重要:Signal(Out(1,X1))=1 ⇔ Signal(In(1, X1)) ≠ Signal(In(2,X1))
1. 确定任务
2. 搜集相关知识
3. 确定谓词、函数和常量的词汇表
4. 对域的通用知识进行编码
5. 对特定问题实例的描述进行编码
6. 把查询提交给推理过程并获取答案
7. 调试知识库
电路领域
- 一位全加器:最初的两个输入是需要相加的两位,第三个输入是一个进位。第一个输出是和,第二个输出是下一个加法器的进位。
1. 确定任务:电路是否相加正确(电路确定)
2. 搜集相关知识:导线和门的组成,门的类型(AND,OR,XOR,NOT),不相关:尺寸、形状、颜色、门的成本
3. 确定词汇表:Type(X1) = XOR, Type(X1,XOR) XOR(X1)
4. 对域的通用知识进行编码
(1). 如果两个接线端是相连的,那么它们具有相同的信号:∀t1,t2 Connected(t1, t2) ⇒ Signal(t1) = Signal(t2)
(2) 每个接线端的信号不是1就是0(不可能两者都是):∀t Signal(t) = 1 ∨ Signal(t) = 0 1 ≠ 0
(3)Connected是一个可交换谓词:∀t1,t2 Connected(t1, t2) ⇒ Connected(t2, t1)
(4)或门的输出为1,当且仅当它的某一个输入为1:∀g Type(g) = OR ⇒ Signal(Out(1,g)) = 1 ⇔ ∃n Signal(In(n,g)) = 1
(5)与门的输出为0,当且仅当它的某一个输入为0:∀g Type(g) = AND ⇒ Signal(Out(1,g)) = 0 ⇔ ∃n Signal(In(n,g)) = 0
(6)异或门的输出为1,当且仅当它的输入是不相同的:∀g Type(g) = XOR ⇒ Signal(Out(1,g)) = 1 ⇔ Signal(In(1,g)) ≠ Signal(In(2,g))
(7)非门的输出与它的输入相反:∀g Type(g) = NOT ⇒ Signal(Out(1,g)) ≠ Signal(In(1,g))
5. 对特定问题实例的描述进行编码
- 首先对门加以分类:Type(X1)=XOR Type(X2)=XOR Type(A1)=AND Type(A2)=AND Type(O1)=OR
- 其次说明门与门之间的连接
Connected(Out(1,X1),In(1,X2)) Connected(In(1,C1),In(1,X1))
Connected(Out(1,X1),In(2,A2)) Connected(In(1,C1),In(1,A1))
Connected(Out(1,A2),In(1,O1)) Connected(In(2,C1),In(2,X1))
Connected(Out(1,A1),In(2,O1)) Connected(In(2,C1),In(2,A1))
Connected(Out(1,X2),Out(1,C1)) Connected(In(3,C1),In(2,X2))
Connected(Out(1,O1),Out(2,C1)) Connected(In(3,C1),In(1,A2))
6. 把查询提交给推理过程并获取答案
- 对于1位全加器有哪些可能的输入与输出组合?
- ∃i1,i2,i3,o1,o2 Signal(In(1, C1)) = i1 ∧Signal(In(2,C1)) = i2 ∧ Signal(In(3,C1)) = i3 ∧Signal(Out(1,C1)) = o1 ∧ Signal(Out(2,C1)) = o2
7. 调试知识库
- 可能省略了断言 1 ≠ 0
- 对异或门(XOR)尤其重要:Signal(Out(1,X1))=1 ⇔ Signal(In(1, X1)) ≠ Signal(In(2,X1))
总结
- 命题逻辑只是对事物的存在进行限定,而一阶逻辑对于对象和关系的存在进行限定,因而获得更强的表达能力。
- 一阶逻辑
- 对象和关系是语义基元
- 语法:常量、函数、谓词、相等、量词
- 语句的真值由一个模型和对句子符号的解释来判定。
- 提高表达能力:足以定义wumpus世界
- 在一阶逻辑中开发知识库是一个细致的过程,包括对域进行分析、选择词汇表、对支持所需推理必不可少的公理进行编码。
- 命题逻辑只是对事物的存在进行限定,而一阶逻辑对于对象和关系的存在进行限定,因而获得更强的表达能力。
- 一阶逻辑
- 对象和关系是语义基元
- 语法:常量、函数、谓词、相等、量词
- 语句的真值由一个模型和对句子符号的解释来判定。
- 提高表达能力:足以定义wumpus世界
- 在一阶逻辑中开发知识库是一个细致的过程,包括对域进行分析、选择词汇表、对支持所需推理必不可少的公理进行编码。