python 机器学习 一元和二元多项式回归 梯度下降算法
python 机器学习 一元和二元多项式回归
一元多项式
一元多项式表达式为:
Y = W T X = [ w 0 + w 1 + ⋯ + w n ] ⋅ [ 1 + x + ⋯ + x n − 1 ] T Y=W^TX=\left[ w_0+w_1+\cdots +w_n \right] \cdot \left[ 1+x+\cdots +x^{n-1} \right] ^T Y=WTX=[w0+w1+⋯+wn]⋅[1+x+⋯+xn−1]T
其中高次项为一次项的高次幂,将该式写为多元表达式:
Y = W T X = [ w 0 + w 1 + ⋯ + w n ] ⋅ [ x 1 + x 2 + ⋯ + x n ] T Y=W^TX=\left[ w_0+w_1+\cdots +w_n \right] \cdot \left[ x_1+x_2+\cdots +x_n \right] ^T Y=WTX=[w0+w1+⋯+wn]⋅[x1+x2+⋯+xn]T
其中,xn=x^(n+1),n=0,1,2…,n-1
这里使用梯度下降算法拟合一元二次多项式方程:
假设其函数(X,Y)的函数映射关系为: h θ ( x ) = θ 0 + θ 0 × x + θ 0 × x 2 h_{\theta}\left( x \right) =\theta _0+\theta _0\times x+\theta _0\times x^2 hθ(x)=θ0+θ0×x+θ0×x2
损失函数选择均平方误差MSE:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta \right) =\frac{1}{2m}\sum_{i=1}^m{\left( h_{\theta}\left( x^{\left( i \right)} \right) -y^{\left( i \right)} \right)}^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
参数θ关于J(θ)的梯度为:
∂ J ∂ θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J}{\partial \theta _j}=\frac{1}{m}\sum_{i=1}^m{\left( h_{\theta}\left( x^{\left( i \right)} \right) -y^{\left( i \right)} \right)}{x_j}^{\left( i \right)} ∂θj∂J=m1i=1∑m(hθ(x(i))−y(i))xj(i)
所以其参数更新公式为:
θ j = θ j − α ∂ J ∂ θ j = θ j − α m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta _j=\theta _j-\alpha \frac{\partial J}{\partial \theta _j}=\theta _j-\frac{\alpha}{m}\sum_{i=1}^m{\left( h_{\theta}\left( x^{\left( i \right)} \right) -y^{\left( i \right)} \right)}{x_j}^{\left( i \right)} θj=θj−α∂θj∂J=θj−mαi=1∑m(hθ(x(i))−y(i))xj(i)
α为学习率
生成数据
待拟合函数为: y = 2 + 3 × x + 2 × x 2 y=2+3\times x+2\times x^2 y=2+3×x+2×x2
使用numpy.random.normal()函数为数据添加噪声,(高斯噪音):
y_noise=np.random.normal(loc=0,scale=1,size=len(x))
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(-2,2,0.2)
def Y():
return 2+3*x+2*x**2 #待拟合函数
y=Y()
##噪音
# x_noise=np.random.normal(loc=0,scale=0,size=len(x)) #可为x添加随机扰动
y_noise=np.random.normal(loc=0,scale=1,size=len(x))
#x=x+x_noise
y=y+y_noise
x_train=np.stack((np.linspace(1,1,len(x)),x,x**2),axis=1) #使用np.stack(将X0,X1,X2)合成待训练数据
y_train=y
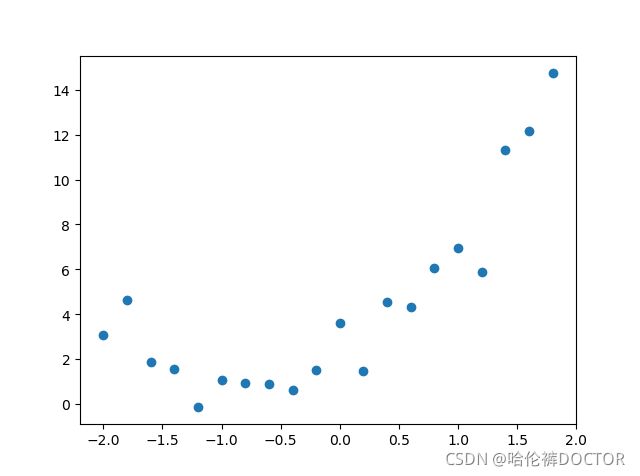
plt.scatter(x,y_train)
plt.show()
x_train的生成原理:
x _ t r a i n = [ x 0 x 1 x 2 ] = [ 1 x x 2 ] x\_train=[x_0\ x_1\ x_2]=[1\ x\ x^2] x_train=[x0 x1 x2]=[1 x x2]

最后使用梯度下降方式实现PYTHON参数更新代码为:
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(-2,2,0.2)
def Y():
return 2+3*x+2*x**2
y=Y()
x_noise=np.random.normal(loc=0,scale=0,size=len(x))
y_noise=np.random.normal(loc=0,scale=1,size=len(x))
x=x+x_noise
y=y+y_noise
x_train=np.stack((np.linspace(1,1,len(x)),x,x**2),axis=1)
y_train=y
plt.scatter(x,y_train)
m=len(x_train)
theat=np.array([0,0,0])
lr=0.009
def Y_pred(x,a):
return a[0]*x[0]+a[1]*x[1]+a[2]*x[2]
def partial_theat(x,y,a):
cost_all=np.array([0,0,0])
for i in range(m):
cost_all=cost_all+(Y_pred(x[i],a)-y[i])*x[i]
return 1.0/m*cost_all
def J(x,y,a):
cost=0
for i in range(m):
cost=cost+(Y_pred(x[i],a)-y[i])**2
return (1/2*m)*cost
iterations=0
theat_list=np.array([0,0,0])
while(True):
# plt.scatter(x_train,y_train)
# plt.plot(np.arange(-3,3,0.1),theat[0]*np.arange(-3,3,0.1)+theat[1])
theat=theat-lr*partial_theat(x_train,y_train,theat)
theat_list=np.vstack((theat_list,theat))
iterations=iterations+1
if(np.abs(J(x_train,y_train,theat_list[-1])-J(x_train,y_train,theat_list[-2]))<0.001):
break
print(theat_list[-1],theat_list.shape)
x_t=np.linspace(-2,2,20)
x_test=np.stack((np.linspace(1,1,20),x_t,x_t**2),axis=1)
##plt.plot(x,theat[0]+x_t*theat[1]+x_t**2*theat[2])
from matplotlib.animation import FuncAnimation
fig,ax=plt.subplots()
atext_anti=plt.text(0.2,2,'',fontsize=15)
btext_anti=plt.text(1.5,2,'',fontsize=15)
ctext_anti=plt.text(3,2,'',fontsize=15)
ln,=plt.plot([],[],'red')
def init():
ax.set_xlim(np.min(x_train),np.max(x_train))
ax.set_ylim(np.min(y_train),np.max(y_train))
return ln,
def upgrad(frame):
x=x_t
y=frame[0]+frame[1]*x+frame[2]*x**2
ln.set_data(x,y)
atext_anti.set_text('a=%.3f'%frame[0])
btext_anti.set_text('b=%.3f'%frame[1])
ctext_anti.set_text('c=%.3f'%frame[2])
return ln,
ax.scatter(x,y_train)
ani=FuncAnimation(fig,upgrad,frames=theat_list,init_func=init)
plt.show()
梯度下降算法拟合过程动图如下:
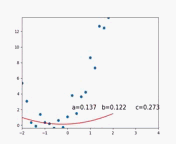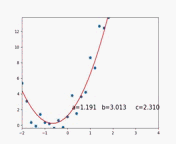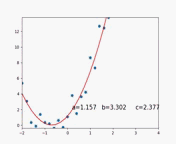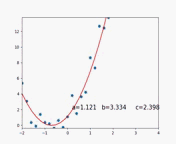
最后拟合结果为: y = 1.86 + 3.07 × x + 1.92 × x 2 y=1.86+3.07\times x+1.92\times x^2 y=1.86+3.07×x+1.92×x2
迭代次数为622次,拟合精度为0.001,拟合效果较好,与原始函数参数产生差距是因为噪声关系。
这里不对代码进行解释,感兴趣的可点击这里,里面有代码的具体解释。
二元多项式
设函数中的二元变量分别为x1和x2,其与y之间的多项式表达式关系为:
y = 5 − 2 x 1 + 3 x 2 + 3 x 1 2 − x 2 2 + 4 x 1 x 2 − 10 x 1 3 y=5-2x_1+3x_2+3{x_1}^2-{x_2}^2+4x_1x_2-10{x_1}^3 y=5−2x1+3x2+3x12−x22+4x1x2−10x13
设该二元函数多项式表达式为:
h θ ( x ) = [ θ 0 ⋮ θ 11 ] T ⋅ [ x 0 x 1 x 2 x 1 x 2 x 1 2 x 2 2 x 1 x 2 2 x 2 x 1 2 x 1 2 x 2 2 x 1 3 x 2 3 ] h_{\theta}\left( x \right) =\,\,\left[ \begin{array}{c} \theta _0\\ \vdots\\ \theta _{11}\\ \end{array} \right] ^T\cdot \left[ \begin{array}{c} x_0\,\,x_1\,\,x_2\,\,x_1x_2\,\,{x_1}^2\\ \,\,{x_2}^2\,\,x_1{x_2}^2\,\,x_2{x_1}^2\,\,\\ {x_1}^2{x_2}^2\,\,{x_1}^3\,\,{x_2}^3\\ \end{array} \right] \,\, hθ(x)=⎣⎢⎡θ0⋮θ11⎦⎥⎤T⋅⎣⎡x0x1x2x1x2x12x22x1x22x2x12x12x22x13x23⎦⎤
将上式中变量用z替换,则原式为:
h θ ( z ) = [ θ 0 ⋮ θ 11 ] T ⋅ [ z 0 z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 z 10 ] h_{\theta}\left( z \right) =\,\,\left[ \begin{array}{c} \theta _0\\ \vdots\\ \theta _{11}\\ \end{array} \right] ^T\cdot \left[ \begin{array}{c} z_0\,\,z_1\,\,z_2\,\,z_3\,\,z_4\,\,z_5\\ \,\,z_6\,\,z_7\,\,z_8\,\,z_9\,\,z_{10}\\ \end{array} \right] hθ(z)=⎣⎢⎡θ0⋮θ11⎦⎥⎤T⋅[z0z1z2z3z4z5z6z7z8z9z10]
参数更新公式和损失函数与一元多项式相同,直接上代码:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
x1=np.linspace(-1,1,20)
x2=np.linspace(2,4,20)
np.random.seed=7
def Y():
return 5-2*x1+3*x2+3*x1**2-x2**2+4*x1*x2-10*x1**3
y=Y()
y_noise=np.random.normal(loc=0,scale=1,size=len(x1))
x_train=np.stack((np.linspace(1,1,len(x1)),x1,x2,x1*x2,x1**2,x2**2,x1*x2**2,x2*x1**2,x1**2*x2**2,x1**3,x2**3),axis=1)#,x1**3,x2**3,x1*x2**3,x1**2*x2**3,x2*x1**3,x2**2*x1**3,x1**3*x2**3
y_train=y+y_noise
features=x_train.shape[1]
m=len(x_train)
theat=np.linspace(1,1,features)*0
lr=0.001
def Y_pred(x,a):
return np.dot(x,a)
def partial_theat(x,y,a):
cost_all=np.linspace(1,1,features)*0
for i in range(m):
cost_all=cost_all+(Y_pred(x[i],a)-y[i])*x[i]
return 1.0/m*cost_all
def J(x,y,a):
cost=0
for i in range(m):
cost=cost+(Y_pred(x[i],a)-y[i])**2
return (1/2*m)*cost
theat_list=np.linspace(1,1,features)*0
while(True):
theat=theat-lr*partial_theat(x_train,y_train,theat)
theat_list=np.vstack((theat_list,theat))
if(np.abs(J(x_train,y_train,theat_list[-1])-J(x_train,y_train,theat_list[-2]))<0.001):
break
print(theat_list[-1],theat_list.shape)
theat_list=theat_list[0:theat_list.shape[0]:500,:]
from matplotlib.animation import FuncAnimation
fig,ax=plt.subplots()
ln,=plt.plot([],[],'red')
def upgrad(frame):
y=np.dot(x_train,frame)
ln.set_data(x1,y)
return ln,
plt.scatter(x1,y_train)
ani=FuncAnimation(fig,upgrad,frames=theat_list,interval=100)
ani.save('二元多项式.gif',writer='pillow')
plt.show()
迭代次数3万多次,计算相对复杂一些,而且与原函数各参数有所不同。
原函数关系:
y = 5 − 2 x 1 + 3 x 2 + 3 x 1 2 − x 2 2 + 4 x 1 x 2 − 10 x 1 3 y=5-2x_1+3x_2+3{x_1}^2-{x_2}^2+4x_1x_2-10{x_1}^3 y=5−2x1+3x2+3x12−x22+4x1x2−10x13
当有噪音时的拟合函数结果为:
h θ ( x ) = [ 0.57550069 − 1.43501733 0.29148473 − 1.05994284 3.24510915 − 0.18548867 0.73316333 3.91299186 − 1.30377424 − 5.8223356 0.17669733 ] T ⋅ [ x 0 x 1 x 2 x 1 x 2 x 1 2 x 2 2 x 1 x 2 2 x 2 x 1 2 x 1 2 x 2 2 x 1 3 x 2 3 ] T h_{\theta}\left( x \right) =\,\,^{\left[ \begin{array}{c} 0.57550069\\ -1.43501733\\ 0.29148473\\ -1.05994284\\ 3.24510915\\ -0.18548867\\ 0.73316333\\ 3.91299186\\ -1.30377424\\ -5.8223356\\ 0.17669733\\ \end{array} \right] ^T\cdot \left[ \begin{array}{c} x_0\,\,x_1\,\,x_2\,\,x_1x_2\,\,{x_1}^2\\ \,\,{x_2}^2\,\,x_1{x_2}^2\,\,x_2{x_1}^2\,\,\\ {x_1}^2{x_2}^2\,\,{x_1}^3\,\,{x_2}^3\\ \end{array} \right] ^T\,\,} hθ(x)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡0.57550069−1.435017330.29148473−1.059942843.24510915−0.185488670.733163333.91299186−1.30377424−5.82233560.17669733⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤T⋅[x0x1x2x1x2x12x22x1x22x2x12x12x22x13x23]T
跟原函数参数有较大差距
当无噪声时,拟合结果为下图,拟合结果与加入噪声时的大致相同,所以,拟合函数结果与假设函数有关。虽然参数有所不同,但是函数误差很小,基本与原函数重合。
为准确拟合原函数,可在损失函数中引入正则项以降低函数复杂度。