scikit-learn机器学习五（逻辑回归与朴素贝叶斯）

逻辑回归

逻辑回归中，响应变量描述了结果是正向情况的概率。如果响应变量等于或者超过了一个区分阈值，则被预测为正向类。

而逻辑函数总是返回一个0-1之间的值

逻辑回归的应用：
垃圾短信的分类： 我们从信息中提取ti-idf特征，并使用逻辑回归对短信进行分类
我们还可以对影评的好坏进行分类：（这是一个多元多类别分类）

我们在sk-learn库中可以使用LogisticsRegression类来进行逻辑回归训练

朴素贝叶斯

贝叶斯定理：使用相关条件的先决知识来计算一个事件概率的公式

sk-learn库中有GaussianNB（高斯朴素贝叶斯）,BernoulliNB（伯努利朴素贝叶斯），MultinomialNB（多项式朴素贝叶斯）三种朴素贝叶斯

多项式朴素贝叶斯适用于类别特征
高斯朴素贝叶斯适用于连续特征
伯努利朴素贝叶斯适用于所有特征为二元值的情形

实战：逻辑回归与朴素贝叶斯的比较

这里我们使用sk-learn库中自带的数据load_breast_cancer来进行训练
这里我们用到了非常常用的划分训练集和测试集的方法train_test_split
最后我们把训练的结果得分由matplotlib进行可视化

具体代码：

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

x,y = load_breast_cancer(return_X_y=True)
x_train, x_test, y_train, y_test = train_test_split(x,y,stratify=y, test_size=0.2, random_state=31)
test1 = LogisticRegression()
test2 = GaussianNB()
score1 = []
score2 = []
train_sizes = range(10, len(x_train), 25)
for size in train_sizes: 
# 逐渐扩大训练集来获得不同训练量下两个模型的性能
    x_slice, _, y_slice, _ = train_test_split(x_train, y_train, train_size=size, stratify=y_train, random_state=31)
    test1.fit(x_slice, y_slice)
    score1.append(test1.score(x_test, y_test))
    test2.fit(x_slice, y_slice)
    score2.append(test2.score(x_test, y_test))

# 可视化
plt.plot(train_sizes, score1, label='LogisticRegression')
plt.plot(train_sizes, score2, label='Naive Bayes')
plt.xlabel('number of training instances')
plt.ylabel('test set accuracy')
plt.legend() # 加图例
plt.show()

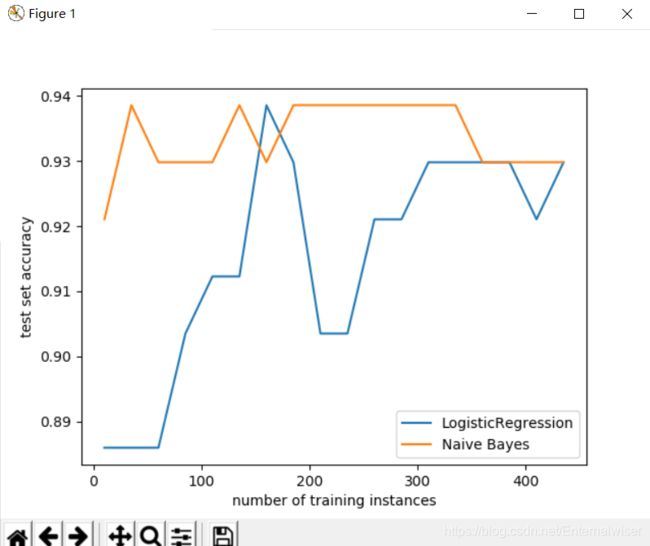
输出结果

可以看到数据规模较小时，朴素贝叶斯分类器的性能比较优越
当数据规模变大时，逻辑回归的性能开始慢慢提升

---

20.8.23补充

这里对逻辑回归再做些补充哈（又学了一次，有些新的收获）

逻辑回归的定义

一种“回归”的分类器，由线性回归演化而来，一种广泛应用于分类问题的回归算法

逻辑回归实际上就是使用联系函数，将线性回归方程进行转换：

线性回归方程：

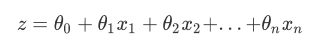
通过Sigmoid函数：

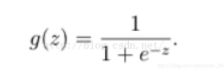
将所有的数据转换为[0, 1]之间 （无限趋近0和1）

然后我们将上面的z带入g(z)中进行简化，我们就可以得到二元逻辑回归的一般形式：

最后我们对线性回归模型的预测结果取
对数几率让其结果无限逼近0和1。

逻辑回归中常用的类

• LogisticRegression : 逻辑回归分类器
• LogisticRegressionCV ： 带交叉验证的逻辑回归分类器
• SGDClassifier ： 梯度下降求解的线性分类器
• SGDRegressor ： 梯度下降正则化后的损失函数的线性回归模型

这里我们讲解最基础的LogisticRegression
（顺带讲解下交叉验证）

损失函数

讲到线性回归的时候应该提过一点点（害太懒了）
逻辑回归的损失函数由最大似然法推导，具体式子：

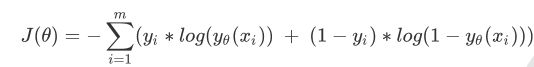
具体数学推导不再赘述（害数学不好）

我们使用损失函数也叫代价函数来衡量参数的优劣——即在测试集上的表现是否良好

当损失函数小时，说明模型在训练集上表现优异；
当损失函数小时，说明模型拟合不足，参数不够好

所以我们通过损失函数来控制拟合不足（泛化能力不够好）的情况

但是我们都知道模型除了拟合不足以外，我们还会有过拟合的状态，在逻辑回归中我们使用正则化来控制模型的过拟合

正则化

我们常听说的惩罚也是来自正则化，一般我们有两种惩罚（penalty）：

• L1
• L2

他们都是通过在损失函数后加上参数的范式的倍数来实现，如下图

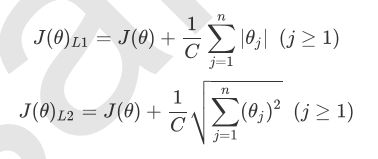
这里有两项，第一项是损失函数，第二项就是两个惩罚的不同——范式

一般我们不取常数参数进行计算，这里的C是一个超参数，一般来说C越小，惩罚越重，正则化效力越强

重点！！！

L1正则化会将不重要的参数置0， 而L2不会（只会趋近0）

逻辑回归的其他重要参数

• solver : 四种算法策略：liblinear lbfgs sag newton-cg

1.一般较小的数据集我们使用liblinear
2.较大的数据集我们使用其余三个
3.超大的数据集我们使用sag

• max_iter : 算法收敛的最大迭代次数

默认是100

其他参数可以参考这篇博文：

Sklearn实现逻辑回归

实战：两种正则化的区别

我们仍然使用load_breast_cancer数据集来进行学习曲线的绘制：

from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 数据的加载
data = load_breast_cancer()
x = data.data
y = data.target

# solver是使用的算法策略，L1只能使用liblinear，L2除了liblinear还可以使用梯度下降策略
# solver:{‘newton-cg’,’lbfgs’,’liblinear’,’sag’,’saga’}
# 默认: ‘liblinear’ 在优化问题中使用的算法
# max_iter=100(默认) : 算法收敛的最大迭代次数
# 这里的C就是我们说的超参数
lrl1 = LR(penalty="l1", solver="liblinear", C=0.5, max_iter=1000)
lrl2 = LR(penalty="l2", solver="liblinear", C=0.5, max_iter=1000)

# 逻辑回归的重要属性coef_，查看每个特征所对应的参数
lrl2 = lrl2.fit(x, y)
lrl1 = lrl1.fit(x, y)
print(lrl2.coef_)
print(lrl1.coef_)

# 四个列表用来存储得分
l1 = []
l2 = []
l1_test = []
l2_test = []

# 训练集和测试集的分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=420)

# np.lispace()前两个参数规定范围，第三个参数是取的个数
# 所以下面就是说从[0.02, 1]之间随机取出25个数
for i in np.linspace(0.02, 1, 25):
	# 我们调整C参数的值绘制曲线
    lrl1 = LR(penalty="l1", solver="liblinear", C=i, max_iter=1000)
    lrl2 = LR(penalty="l2", solver="liblinear", C=i, max_iter=1000)
    # 将得分添加到列表
    lrl1 = lrl1.fit(x_train, y_train)
    # accuracy_score()两个参数，一般填入y的预测值和实际值
    l1.append(accuracy_score(lrl1.predict(x_train), y_train))
    l1_test.append(accuracy_score(lrl1.predict(x_test), y_test))
    lrl2 = lrl2.fit(x_train, y_train)
    l2.append(accuracy_score(lrl2.predict(x_train), y_train))
    l2_test.append(accuracy_score(lrl2.predict(x_test), y_test))

# 使用matplotlib进行实例化
graph = [l1, l2, l1_test, l2_test]
color = ["green", "black", "red", "blue"]
label = ["L1", "L2", "L1_test", "L2_test"]

# 规定画布大小
plt.figure(figsize=(8, 8))

for i in range(len(graph)):
    plt.plot(np.linspace(0.02, 1, 25), graph[i], color[i], label=label[i])
    
plt.legend()
plt.title("Difference between L1 and L2")
plt.ylabel("Scores")
plt.xlabel("Value of C")
plt.show()

我们先看输出结果：

[[ 1.61538297e+00  1.02313837e-01  4.80876166e-02 -4.46179116e-03
  -9.44039119e-02 -3.01456060e-01 -4.56317796e-01 -2.22624403e-01
  -1.35942213e-01 -1.93988281e-02  1.58430227e-02  8.85192776e-01
   1.18955775e-01 -9.46472011e-02 -9.84012568e-03 -2.35225444e-02
  -5.70150907e-02 -2.70449403e-02 -2.77929242e-02  2.34246606e-04
   1.26123273e+00 -3.01768987e-01 -1.72568144e-01 -2.21620160e-02
  -1.73685380e-01 -8.78991654e-01 -1.16355518e+00 -4.28212549e-01
  -4.21484675e-01 -8.69878596e-02]]
  
[[ 4.0081829   0.03219333 -0.13817057 -0.01623763  0.          0.
   0.          0.          0.          0.          0.          0.50581498
   0.         -0.07128791  0.          0.          0.          0.
   0.          0.          0.         -0.24612951 -0.12868192 -0.01439616
   0.          0.         -2.03235123  0.          0.          0.        ]]

第一个矩阵是L2返回的系数，可以看到没有一个是0，虽然有很多都趋向0

第二个矩阵是L1返回的系数，可以看到有的特征的系数为0

ps:该数据有30个特征，所以会返回30个系数

最后我们可以看到绘制的图：

我们可以得到以下信息：

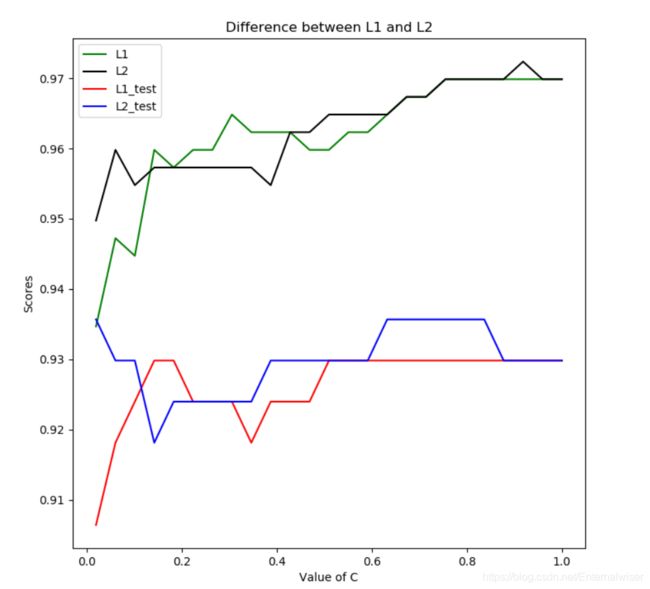
1. 在训练集上的拟合效果好于测试集
2. 随着C值的增加L1,L2在训练集上的得分在增加并逐渐逼近0.97
3. 随着C值得增加L1,L2在测试集上得得分也在增加并逼近0.93
4. 为了取得最好的拟合结果，我们最后选择参数penalty=L2,C=0.7

感谢您的耐心阅读，努力成为自己想要成为的人吧！