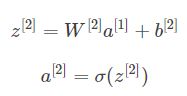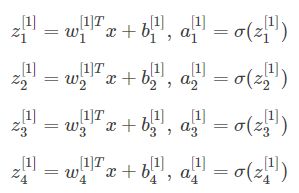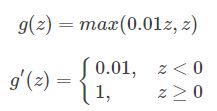1-3 Coursera吴恩达《神经网络与深度学习》第三周课程笔记-浅层神经网络
记录吴恩达深度学习专项课程笔记,方便之后回顾,共5门课,这是第一门课《神经网络与深度学习》第三周浅层神经网络的课程笔记,那我们开始吧。
课程1-2神经网络基础的内容比较简单,主要介绍了神经网络的基础——逻辑回归和向量化,同时介绍了一些python相关编程技巧。
目录
《3.1神经网络概览》Neural Networks Overview
《3.2神经网络表示》Neural Network Representation
《3.3计算神经网络的输出》Computing a Neural Network’s Output
《3.4多个例子中的向量化》Vectorizing across multiple examples
《3.5向量化实现的解释》Explanation for Vectorized Implementation
《3.6激活函数》Activation functions
《3.7为什么需要非线性激活函数?》Why do you need non-linear activation functions
《3.8激活函数的导数》Derivatives of activation functions
《3.9神经网络的梯度下降法》Gradient descent for neural networks
《3.10(选修)直观理解反向传播》Backpropagation intuition(optional)
《3.11随机初始化》Random Initialization
Summary
《3.1神经网络概览》Neural Networks Overview
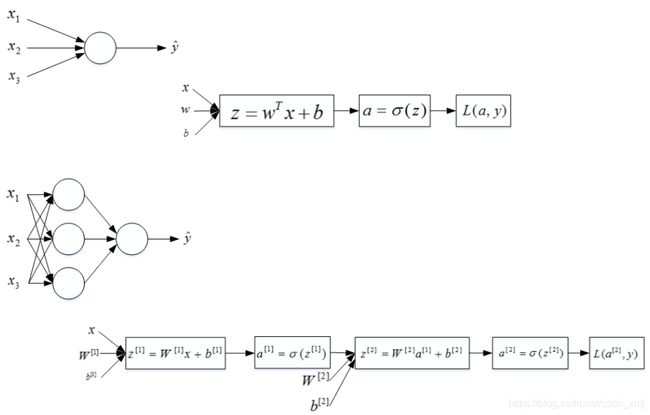
什么是神经网络?What is a Neural Network?如下图:
神经网络的结构与逻辑回归类似,只是神经网络的层数比逻辑回归多一层,多出来的中间那层称为隐藏层或中间层。从计算上来看,神经网络的正向传播和反向传播比logistic回归多了一次重复的计算。引入新的标签:方括号上标[i]表示当前所处的层数;圆括号上标(i)表示第i个样本。
正向传播过程分成两层,第一层是输入层到隐藏层,用上标[1]来表示:
第二层是隐藏层到输出层,用上标[2]来表示:
同样,反向传播过程也分成两层。第一层是输出层到隐藏层,第二层是隐藏层到输入层。接下来的视频中,我们会慢慢讲解细节。
《3.2神经网络表示》Neural Network Representation
下面我们讲解只有一个隐藏层的神经网络,这是一张神经网络结构图:
我们命名一下这张图的各个部分。输入特征x1,x2,x3竖向堆叠起来,这是神经网络的输入层(input layer),顾名思义它包含了神经网络的输入;然后这里有另外一层的圆圈,称之为神经网络的隐藏层(hidden layer);最后这里是输出层(output layer),只有一个节点,它负责输出预测值y帽。在一个神经网络中,当你使用监督学习训练它时,训练集包含了输入x,还有目标输出y。“隐藏层”的含义是在训练集中这些中间节点的真实数值我们是不知道的,看不到它们的数值。
现在我们再引入几个符号,之前我们用向量x表示输入特征,另一种表达方式a^[0],而a也表示激活(activations)的意思,它意味着网络中不同层的值会传递给后面的。把隐藏层输出记为a^[1],上标从0开始。用下标表示第几个神经元,注意下标从1开始。例如a^[1]_1表示隐藏层第1个神经元(节点)。在python中,隐藏层有4个神经元就可以写成下面矩阵的形式:
最后的输出层会产生某个数值a^[2],是个实数。
当我们在计算网络的层数时,不算输入层的原因是:隐藏层是第一层,输出层是第二层,在我们约定的符号中将输入层称为第零层。所以上面的例子可以说这是一个“三层的”神经网络,因为它有输入层、隐藏层和输出层。当你在研究论文时发现,一般称为双层神经网络,因为我们不把输入层看作一个标准的层。最后我们要知道隐藏层和输出层是带有参数的,这里隐藏层有两个相关参数W和b,使用上标[1]表示这些参数。之后会细讲。
关于隐藏层对应的权重W^[1]和常数项b^[1],W^[1]的纬度是(4,3)。这里4对应着隐藏层神经元个数,3对应输入层特征向量x的元素个数。常数项b^[1]的纬度是(4,1),4也对应着隐藏层神经元个数。输出层对应的权重W^[2]和常数项b^[2],W^[2]的纬度是(1,4)。这里1对应着输出层神经元个数,4对应隐藏层特征向量x的元素个数。常数项b^[2]的纬度是(1,1),因为输出只有1个神经元。总结:第i层的权重W^[i]维度的行等于i层神经元的个数,列等于i-1层神经元的个数;第i层常数项b^[i]的行等于第i层神经元的个数,列始终为1。
《3.3计算神经网络的输出》Computing a Neural Network’s Output
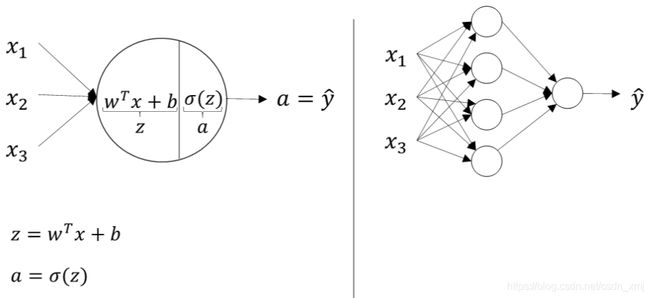
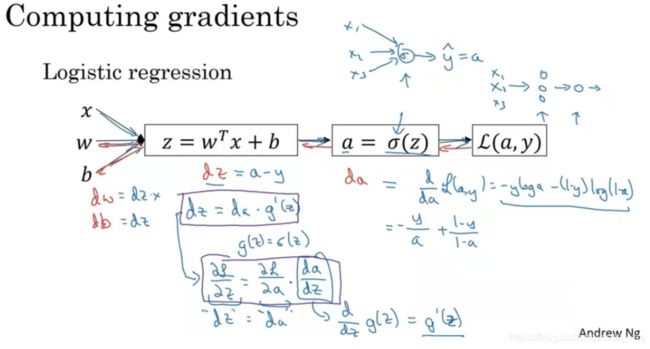
接下来我们开始详细推导神经网络的计算过程。我们前面讲过两层神经网络可以看成是逻辑回归再重复计算一次。如下图所示,逻辑回归的正向计算可以分解成计算z和a的两部分:
下面的圆圈代表了回归计算的两个步骤,神经网络重复计算这些步骤很多次:
对于两层神经网络,从输入层到隐藏层对应一次逻辑回归运算;从隐藏层到输出层对应一次逻辑回归运算。每层计算时,要注意对应的上标和下标,一般我们记上标方括号表示layer,下标表示第几个神经元。例如a^[l]_i表示第l层的第i个神经元。注意,i从1开始,l从0开始。
下面,我们将从输入层到输出层的计算公式列出来:(共4个隐藏单元)
需要弄清楚符号,大写T表示向量转置。
然后,从隐藏层到输出层的计算公式为:
上述每个节点的计算都对应着一次逻辑运算的过程,分别由计算z和a两部分组成。
我们需要将等式向量化,提高效率:
当我们向量化时一条经验法则可以帮助你找到方向:当我们这一层有不同的节点,那就纵向地堆叠起来。
所以我们看下一张幻灯片:
当你有一个单隐层神经网络,你需要用代码实现的是右边四个等式。这里W^[1]的维度是(4,3),b^[1]的维度是(4,1),W^[2]的维度是(1,4),b^[2]的维度是(1,1)。
《3.4多个例子中的向量化》Vectorizing across multiple examples
上个视频讲解了已知单个训练样本时,计算神经网络的预测,在这个视频中,将看到如何将不同训练样本向量化。
在书写标记上用上标(i)表示第i个样本,例如x^(i),z^(i),a^[2](i)。我们看下一张幻灯片,把上面的for循环写成矩阵运算的形式:
注意:Z^[1] = W^[1]X + b^[1],A^[1] = sigma(Z^[1]),Z^[2] = W^[2]A^[1] + b^[2],A^[2] = sigma(Z^[2]),其中Z^[1]纬度是(4,m),4是隐藏层神经元的个数;A^[1]的纬度与Z^[1]相同;Z^[2]和A^[2]的纬度均为(1,m)。
就好比把x向量堆叠到矩阵各列构成X矩阵,对于z你也可以做同样的事情。矩阵的行表示神经元个数,列表示样本数目m。这些矩阵,比如说Z和A,横向的话我们对所有训练样本用指标排序,所以横向对应了不同的训练样本,从左往右就扫过整个训练集,而竖向指标就对应神经网络的不同节点,这是隐藏单元的指标。
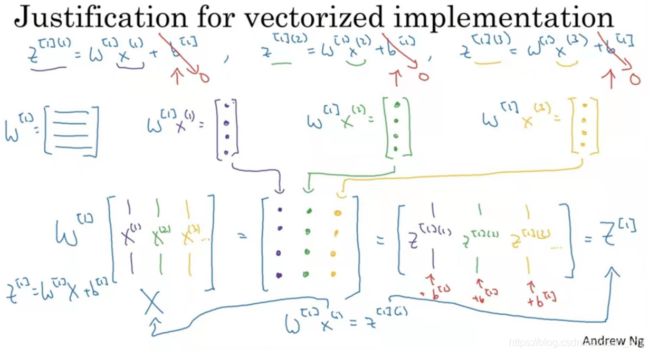
《3.5向量化实现的解释》Explanation for Vectorized Implementation
这个视频解释为什么我们写下的方程向量化在多样本时的正确实现。(不同颜色加以区分)
这里说明了为什么Z^[1]=W^[1]+b^[1],这是求解四个等式中的第一步,然后你会发现其他的类似推导。
这里注意一下输入矩阵X也可以写成A^[0]。
《3.6激活函数》Activation functions
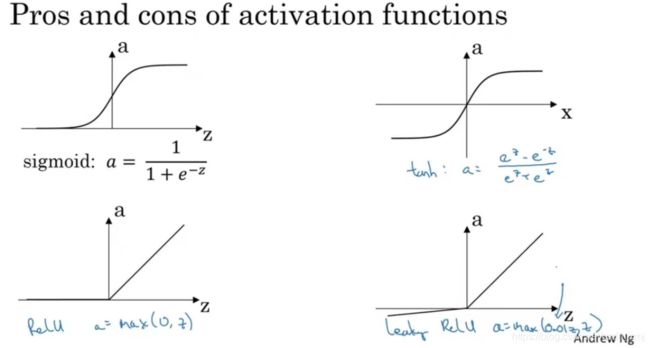
在隐藏层和输出层可以选择激活函数,目前为止我们用的是sigma激活函数,但有时其他函数效果要好的多。我们看一些可供选择的函数。不同的激活函数有各自的优点。下面我们就来介绍几个不同的激活函数g(x)。
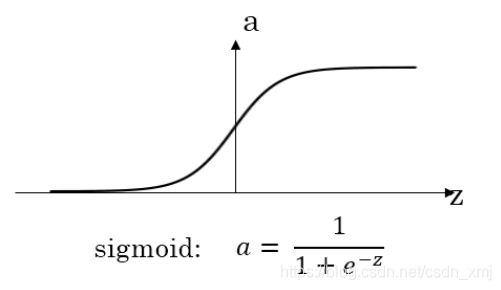
sigmoid函数-(0,1)
tanh函数(双曲正切函数)-(-1,1)
此时激活函数的平均值更接近0,类似数据中心化的效果,使数据平均值接近0,这实际让下一层的学习更方便一点。这个会在第二门课详细讨论,但你要记住这一点,我几乎不用sigma激活函数了。使用sigma函数的例外是二分类。在这个例子中,可以隐藏层用tanh函数,输出层用sigma函数。现在sigma函数和tanh函数都有一个缺点,如果z非常大或非常小时,那么导数的梯度(函数的斜率)可能就很小,接近0,这样会拖慢梯度下降算法。
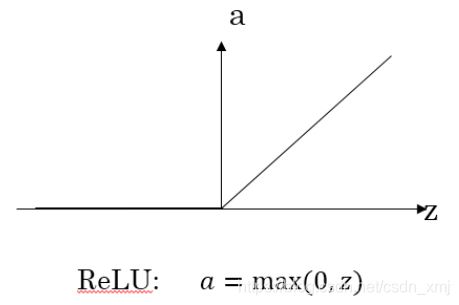
ReLU函数(修正线性单元)-机器学习最受欢迎的工具
只要z为正,导数就是1;当z为负时,斜率为0。在选择激活函数时有一些经验法则,如果你的输出是0和1(二元分类),那么sigma函数很适合作为输出层的激活函数,然后其他所有单元都用ReLU函数,这是今天大多数人都在用的。ReLU的缺点是当z为负时,导数为0,但还有一个版本,带泄露的ReLU。
Leaky ReLU函数(泄漏的ReLU)
Andrew快速回顾这几个激活函数:
1.sigmoid函数除非用在二元分类的输出层,不然绝对不要用,或者几乎从来不用。
2.tanh函数几乎在所有场合都更优越。
3.最常用的默认激活函数是ReLU,如果你不确定用哪个,你就用这个,或者也可以试试带泄漏的ReLU。你可能会问为什么是0.01,可以把它设成学习函数的另一个参数,有人说这样效果更好,但很少见人这样做,你可以在你的应用中使用,如果效果好,你可以一直用它。
深度学习的一个特点是在建立神经网络时经常有很多不同的选择,比如隐藏单元数、激活函数,还有如何初始化权重(接下来会讲)。对于你的应用,事实上很难预先准确地知道什么参数最有效,所以Andrew建议如果你不确定哪种激活函数最有效你可以先试试在你的保留交叉验证数据集上或者开发集上跑,看看哪个参数效果好,就用哪个。你可以搭建具有前瞻性的神经网络架构,可以对你问题的特质更有针对性,让你的算法迭代更加流畅。
经常会有人问:为什么要使用激活函数呢?激活函数如何选择?下个视频将解释。
《3.7为什么需要非线性激活函数?》Why do you need non-linear activation functions
我们知道上一部分讲的四种激活函数都是非线性(non-linear)的。那是否可以使用线性激活函数呢?答案是不行!下面我们就来进行简要的解释和说明。
如果你用线性激活函数(恒等激活函数),那么神经网络只是把输入线性组合再输出(假设激活函数为g(z)=z,经过推导我们发现a^[2]仍是输入变量x的线性组合)。事实证明,如果你使用线性激活函数或者没有激活函数,那么无论你的激活函数有多少层,一直在做的只是计算线性激活函数,所以不如去掉全部隐藏层。使用神经网络与直接使用线性模型的效果并没有什么两样。因此,隐藏层的激活函数必须要是非线性的。如果所有的隐藏层全部使用线性激活函数,只有输出层使用非线性激活函数,那么整个神经网络的结构就类似于一个简单的逻辑回归模型。只有一个地方可以用线性激活函数g(z)=z,如果你要机器学习的是回归问题,所以y是实数,比如预测房价,y是实值,那么输出层用线性激活函数也许可行,但是隐藏层不能用线性激活函数。具体情况,具体分析。
《3.8激活函数的导数》Derivatives of activation functions
在梯度下降反向计算过程中少不了计算激活函数的导数即梯度。
我们先来看一下sigmoid函数的导数:
对于tanh函数的导数:
具体函数和导数图像如下:
对于ReLU函数的导数:
对于Leaky ReLU函数:
《3.9神经网络的梯度下降法》Gradient descent for neural networks
在这个视频中,你将看到梯度下降法的具体实现,如果处理单隐层神经网络。将介绍为什么特定的几个方程是精准的方程,或者可以针对你的神经网络实现梯度下降的正确方程。
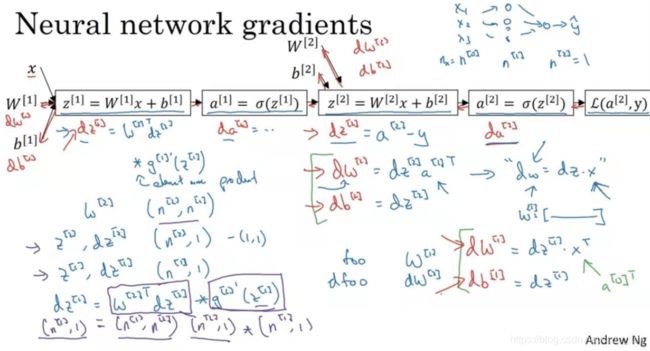
随机初始化参数很重要,而不是全部初始化为0。总结一下正向传播过程。
反向传播是计算导数或者梯度的过程,成本函数对各个参数的梯度如下(非板书版):
python中加入keepdim=True防止输出古怪的秩为1的数组,确保python输出的是矩阵。*乘积表示两个矩阵的逐元素乘积。还有一种方法不使用keepdim参数,显示的调用reshape把np.sum输出结果写成矩阵形式。下个视频讲解我们是如何导出反向传播算法的六个式子的(选修)。
反向传播的具体推导过程我们下一部分在进行详细说明。
《3.10(选修)直观理解反向传播》Backpropagation intuition(optional)
我们仍然使用计算图的方式来推导神经网络反向传播过程。记得之前介绍逻辑回归时,我们就引入了计算图来推导正向传播和反向传播,其过程如下图所示:
下面是神经网络,多一个隐藏层。
对于单个训练样本,正向过程很容易,反向过程可以根据梯度计算方法逐一推导。
我们不需要对输入x求导,因为监督学习的输入x是固定的,我们不优化x,所以就不对x求导(至少对于监督学习是这样)。
总结一下,浅层神经网络(包含一个隐藏层),m个训练样本的正向传播过程和反向传播过程分别包含了6个表达式,其向量化矩阵形式如下图所示:
总之,正向传播和反向传播有如下形式:
最好记住这种图片,之后会经常碰到。
《3.11随机初始化》Random Initialization
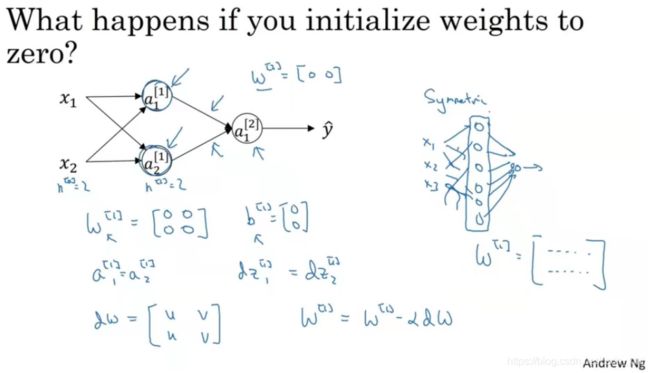
当你训练神经网络时,随机初始化权重很重要,对于logistic回归,可以将群组初始化为零,但如果神经网络的各参数数组全部初始化为0,再使用梯度下降算法,那会完全无效。来看一下为什么。
你有两个输入特征,设置W和b为零,导致两个神经元得到相同的结果,因为两个隐藏单元都在做完全一样的计算;当你计算反向传播时,出于对称性结果也是相同的。技术上假设输出的权重也是一样的,意味着节点计算完全一样的函数,完全对称。可以通过归纳法证明。在这种情况下,多个隐藏单元没有意义。对于多个输入特征也是一样的。
解决方法也很简单,就是将W进行随机初始化(b可初始化为零)。python里可以使用如下语句进行W和b的初始化:
W_1 = np.random.randn((2,2))*0.01 #随机初始化
b_1 = np.zero((2,1))
W_2 = np.random.randn((1,2))*0.01
b_2 = 00.01怎么来的?实际上我们通常把权重矩阵初始化成非常小非常小的随机值,因为如果使用tanh函数或sigmoid激活函数,权重太大是计算出来的值可能落在平缓部分,梯度的斜率非常小,意味着梯度下降法会非常慢,学习过程也会非常慢。下周的学习将讲解选取0.01以外的数,但不管怎样,初始化参数一般都很小。
总结:在这周的视频中你知道如何设立单隐层神经网络,初始化参数,并用正向传播计算预测值,还有计算导数,然后使用梯度下降反向传播。
Summary
本节课主要介绍了浅层神经网络。首先,我们简单概述了神经网络的结构:包括输入层,隐藏层和输出层。然后,我们以计算图的方式推导了神经网络的正向输出,并以向量化的形式归纳出来。接着,介绍了不同的激活函数并做了比较,实际应用中根据不同需要选择合适的激活函数。激活函数必须是非线性的,不然神经网络模型起不了任何作用。然后,我们重点介绍了神经网络的反向传播过程以及各个参数的导数推导,并以矩阵形式表示出来。最后,介绍了权重随机初始化的重要性,必须对权重W进行随机初始化操作。
说明:记录学习笔记,如果错误欢迎指正!转载请联系我。