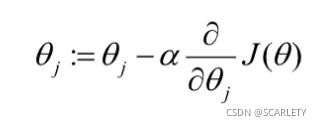吴恩达机器学习第二次作业-逻辑回归（python实现）

        这次作业的目的是运用课程上所学的逻辑回归方法（是二元分类问题）以及正则化处理方法的应用。这篇blog记录的我作业答案以及在做作业过程中遇到的一些问题(程序大部分是自己编写的,如果有同学熟悉pandas和scipy,有一些功能是可以调用这些工具包里面的标准函数实现的)。

 

        欢迎各位同学一起交流学习，如有错误欢迎批评指正。

一、回顾一下逻辑回归与正则化处理的主要内容

1、逻辑回归

（1）分类问题

与回归拟合问题不同，分类问题指的是预测结果是否属于某一个类别；

使用的算法就叫做逻辑回归。

（2）二元分类问题与逻辑回归算法

因变量只属于两类之一，用0和1表示。

逻辑回归的过程：

• 预测结果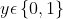,特征为
• 做出假设函数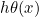,要求
• 设置阈值T（如T=0.5）,

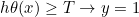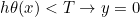
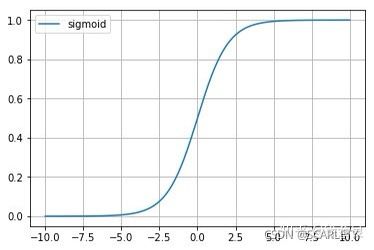
(3)假设函数的表示

假设函数：,表示转置，由于,因此选择sigmoid函数作为g（z）

图像如下：

 假设函数的作用：可以理解为根据选择的参数计算输出变量y=1的概率。

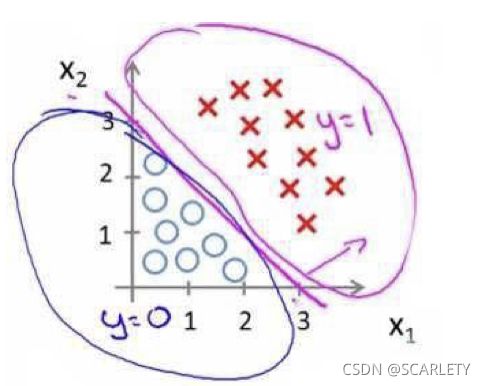
（4）判定边界（Decision Boundary）

 上面两张图直观地表示了什么是判定边界，其实逻辑回归做的事情就是计算出一个判定边界，将不同类的数据区分开来。

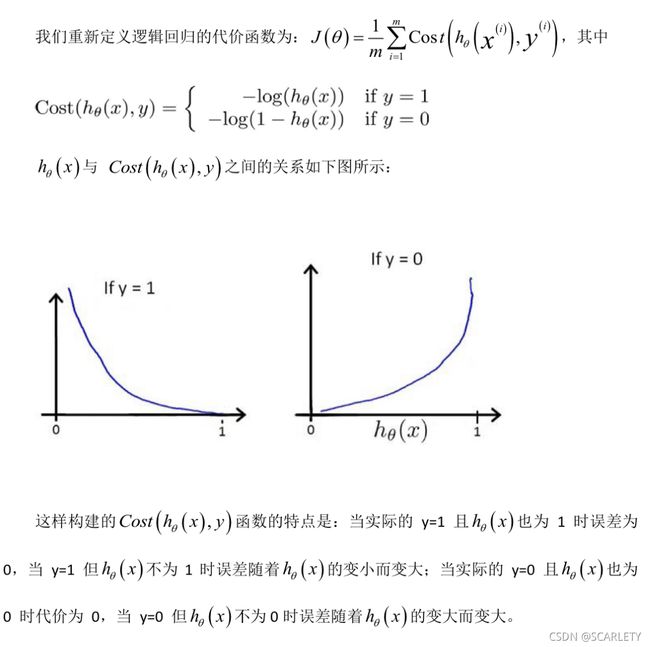
（5）代价函数

为了解决构造地代价函数是非凸函数的问题。

 简化地代价函数：

 然后是进行参数更新（如果需要的话，特征放缩依然很有效）：

 （6）一对多分类问题

当预测类别大于2时，我们依然可以将其转化为二元分类问题，采用“一对其余”地方式进行，最后分别计算每一个分类器中相应类别地概率，最后取概率最大的那一类作为输出。

2、正则化

（1）作用

解决过拟合问题（数据降维的方法（如PCA）也可以解决过拟合问题）

（2）思想

决策边界产生过拟合的原是，特征的高次项作用过大。因此我们要解决过拟合问题可以适当减小高次项的系数，正则化就是减小高次项系数的方法。

（3）做法

引入正则化惩罚项，对系数进行惩罚，减小高次项的作用。下面是正则化代价函数：

这里的 叫做正则化参数，和学习率一样也是一个超参数。

 参数更新（注意这里不参与正则化操作）：

二、作业的要求的分析与实现

1、前半部分二元分类问题

（1）作业要求

• 数据可视化
• 编写sigmoid函数
• 编写代价函数与梯度
• 使用相关算法进行参数学习（作业中推荐用octave中fminunc函数进行优化，这里我依然使用最原始的批量梯度下降法）
• 评估本次逻辑回归结果（绘制决策边界；将训练数据用于测试计算准确率）

（2）分析与实现

• 数据可视化

这部分内容我统一编写在plotdata.py的文件中,在PlotData类中实现.

首先需要读取数据并进行初步处理,这里我编写了getdata()方法,主要是以逗号作为分隔符按行读取ex2data1.txt和ex2data2.txt中的数据,将其分别储存在特征矩阵x和真实值矩阵y中,相应部分代码如下(完整代码在后面附录中):

    def get_data(self):
        '''获得特征矩阵和真实值矩阵'''
        with open(self.filename, 'r') as fob:
            contents = fob.readlines()
            nums_comma = contents[0].count(",")#获取逗号数量
            nums_data = len(contents)          #获取数据维度
            x = np.zeros((nums_comma, nums_data), np.float32)
            y = np.zeros((1, nums_data), np.float32)
            for i in range(nums_data):
                l = [j for j in contents[i].split(",")]  # .split()函数分割数据,将以逗号分隔的数据储存在l列表中
                for w in range(nums_comma):               #前面nums_comma个数据是特征
                    x[w][i] = l[w]
                y[0][i] = l[nums_comma].replace("\n", "") #最后一个是结果真实值
        if __name__ == "__main__":#文件内运行用于测试
            print(contents)
            print(x)
            print(y)
        return x, y

然后根据相应特征和真实值矩阵绘制训练数据图,编写方法plot_training_data()方法实现:

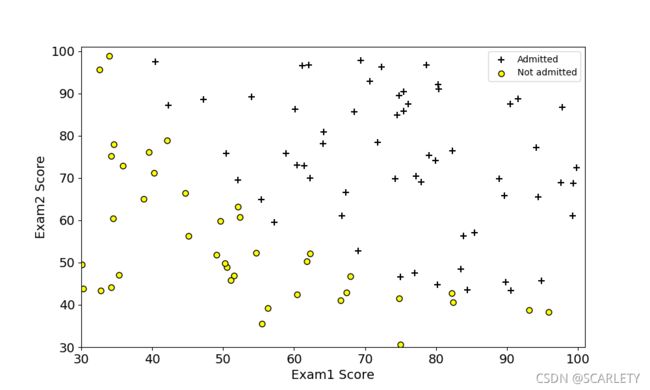
•     def plot_training_data(self, figname="TrainingData.png", theta= None,deci_boundary = False):
          '''可视化训练集并绘制决策边界，需要给出保存图片的名称和训练好的系数矩阵theta，deci_boundary决定是否绘制决策边界'''
          x, y = self.get_data()
          figure1 = plt.figure(figsize=(10, 6))
          for i in range(len(y[0])):
              if y[0][i] == 1:
                  f1 = plt.scatter(x[0][i], x[1][i], marker='+', c="black", label="Admitted", s=50)
              else:
                  f2 = plt.scatter(x[0][i], x[1][i], marker='o', c="yellow", edgecolor="black", label="Not admitted",
                                   s=40)

对于ex1.data1的训练数据图为:

•  sigmoid函数

编写sigmoid函数很简单几行代码就能搞定:

 @staticmethod
    def sigmoid(X):
        '''Sigmoid函数，需要一个数组参数X'''
        g = 1/(1+np.exp(-X))   #X可以是数组，返回一个对应维数的结果数组
        return g

• 编写代价函数与梯度

代价函数的编写要充分利用向量化方法进行运算,能有效减少代码数量(可以看到向量化的代码两行搞定，细节我就不展开了，可以体会一下代码):

    def cost_func(self):
        '''计算代价函数'''

        h_theta = self.sigmoid(np.dot(self.theta,self.X))
        #避免np.log计算值过大采用np.log(data + 1e-5)来避免产生inf项
        J_theta = (np.vdot(self.y,np.log(h_theta+1e-5).T) + np.vdot((1-self.y),np.log(1-h_theta +1e-5).T))/(-self.m)
        return h_theta,J_theta

•  使用相关算法进行参数学习(这里我依然使用批量梯度下降法实现）

主要 代码就这两行（详细代码见附录） 

 partial_theta = np.dot((h-self.y),self.X.T)/self.m
            self.theta = self.theta - self.alpha*partial_theta

根据以上公式，将参数初始化为0，反复更新迭代，这次作业视频中提到使用批量梯度下降法的迭代收敛速度很慢，对学习率的要求也很高，本次作业我选择学习率alpha=0.04，迭代步数40万步。迭代收敛图如下：

 

 从迭代曲线中我们可以发现在前20万步时是震荡收敛的，20万步以后才逐渐收敛到一个最小值（可能是局部最小值）

本算法优化出来的参数theta=[-24.293768     0.19929314   0.19445102]

参考最优                     theta=[25.16227358     0.20623923     0.20147921]

 对比发现批梯度下降法优化出来的结果与最优结果很接近，我推测批梯度下降法收敛到了局部最小值。

• 评估本次逻辑回归结果（绘制决策边界；将训练数据用于测试计算准确率）

首先是绘制决策边界，我们选择0.5作为分类阈值，因此这里的决策边界就是sigmoid函数g（z）=0.5，即z=0。

也就是说，最终是直线,决策边界图如下：

 然后是使用训练数据集再次作为测试数据集来计算所求模型的分类准确度。这里有一个小trick，我将预测结果矩阵和真是矩阵相减，再数里面有多少个0就是预测正确的数量。运行结果（详细代码见附录evaluate_logistic_reg.py)：

 可以看到，总的正确率是89%，这个数据和参考最优化参数theta做出的分类一致，这证明批量梯度下降法依然很有用。

2、后半部分带正则化的二元分类问题

（1）作业要求

• 数据可视化
• 特征映射
• 正则化代价函数与梯度
• 使用相关算法进行参数学习（作业中推荐用octave中fminunc函数进行优化，这里我依然使用最原始的批量梯度下降法）
• 绘制正则化参数lambda取0、1、100时的决策边界

（2）分析与实现

• 数据可视化

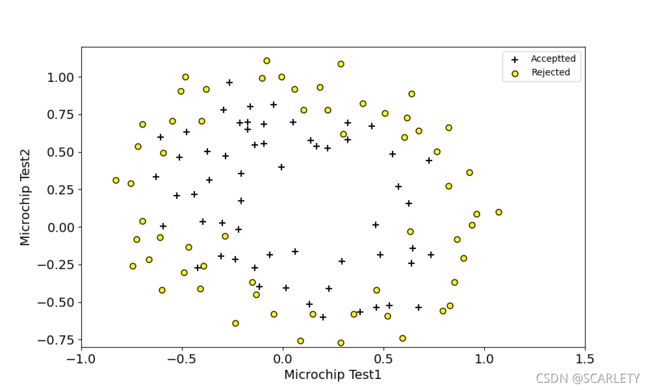
这里和前半部分没什么区别，直接拿来用就可以，下面是结果图：

• 特征映射

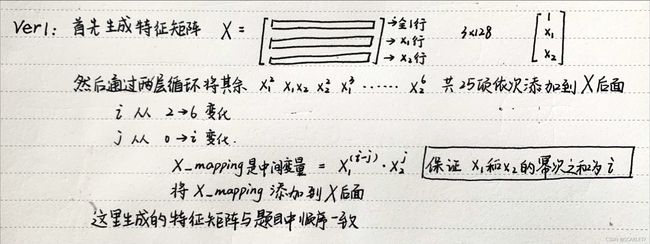
我们可以看到数据的特征依然是两个：x1和x2，但是显然这次的决策边界必须用非线性曲线来表示 ，因此我们要添加高次多项式来增加决策边界的非线性。题目中要求我们添加到6次项，因此特征向量的维数共28维。

 本次作业我应用了两种特征映射的算法，两种方法生成的特征矩阵的区别在于多项式的排列顺序不同：

第一种：

      def mapping_ver1(self):
        '''这是第一种映射方法'''
        X = np.append(np.ones((1,self.m),np.float32),self.x,axis=0) #按列添加
        if self.degree >= 2:
            for i in range(2,self.degree+1):
                for j in range(i+1):
                    x_mapping = np.multiply(np.power(self.x[0],i-j),np.power(self.x[1],j))#x_mapping 是118维向量,np.multiply()是矩阵对应元素相乘，np.dot()是矩阵乘法
                    x_mapping_match = np.tile(x_mapping,(1,1))            #将x_mapping变成1*118的矩阵与X维数相匹配
                    X = np.append(X,x_mapping_match,axis=0)  #axis=0表示按列方向（也就是垂直方向添加）
        x_mapped = X
        return x_mapped

 第二种：

    def mapping_ver2(self):
        '''这是另一种映射方法'''
        X = np.ones((1,self.m))
        for i in range(self.degree+1):
            for j in range(self.degree-i+1):
                x_mapping = np.multiply(np.power(self.x[0], i), np.power(self.x[1],j))  # x_mapping 是118维向量,np.multiply()是矩阵对应元素相乘，np.dot()是矩阵乘法
                x_mapping_match = np.tile(x_mapping, (1, 1))  # 将x_mapping变成1*118的矩阵与X维数相匹配
                X = np.append(X, x_mapping_match, axis=0)
        X = np.delete(X,0,axis=0) #删除第一行
        x_mapped = X
        return x_mapped

•  正则化代价函数与梯度

这里我们只需要再前半部分作业的基础上做修改即可，也就是添加正则化惩罚项，以及注意正则化的细节，theta0不参与正则化惩罚。

 

 

就是实现上面两个公式，这里再强调一下向量化的重要性 ，以及本次的方法依然是批梯度下降法。不过这部分使用批梯度下降法很快，选择学习率alpha=0.1，迭代步数4000步即可，正则化系数lambda=1。迭代曲线如下：

这里我用的是第二种特征映射，如果使用第一种映射，那么得到theta的顺序会不一样，需要特别注意一下 。

获得的参数theta：

[ 1.26660432 ， 1.17785322， -1.41400304， -0.17448499， -1.19068506，

-0.46250991，  -0.93134692 ， 0.62210174 ，-0.90854099， -0.35892507，

-0.27216834 ，-0.29425143，  -0.14224715， -2.01088208， -0.36507628，

-0.6138938 ， -0.27610597， -0.32644826，0.12349772， -0.05547685，

-0.04860702，  0.01295063， -1.45638986， -0.20727613，-0.29248375，

-0.24131965，  0.02411789， -1.04302262]

参考最优theta：

[ 1.27273981,  1.18108974, -1.43166669, -0.17513036, -1.19281478,
 -0.45635758, -0.9246528 ,  0.62527237, -0.9174247 , -0.35723884,
 -0.27470605, -0.29537769, -0.14388711, -2.0199599 , -0.36553508,
 -0.61555685, -0.27778507, -0.32738029,  0.12400668, -0.05098942,
 -0.04473108,  0.01556645, -1.45815829, -0.20600596, -0.29243192,
 -0.24218804,  0.02777165, -1.04320421]

对比发现，我们得到的与参考theta相差不大，说明梯度下降法依然有效。

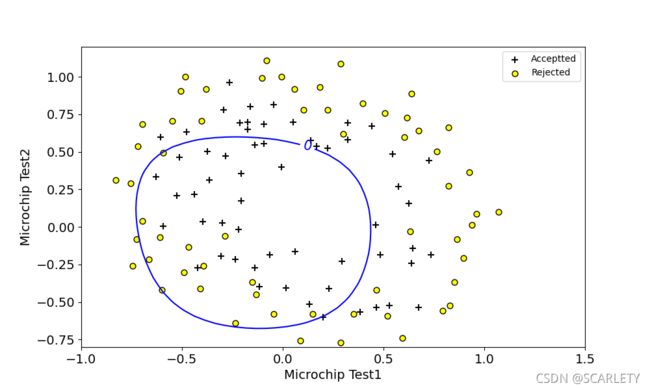
• 绘制正则化参数lambda取0、1、100时的决策边界

这里绘制决策边界我使用了等高线的方法（代码见附录plotdata.py)，这个trick有几个点需要注意一下：

设横轴为U，纵轴为V，高度为Z

第一，等高线的三个参数都要是2维的，因此需要用np.meshgrid()来将坐标轴变换成相应格式；

第二，注意Z矩阵的排列顺序，要重左上角从上往下依次排列。

以上这两点是我经过多次调试发现的问题，就是说我得到了最优化的参数theta但是决策边界绘制与参考的差距比较大，如果遇到和我相同问题的同学，我相信这两个注意事项会很有帮助。

下面给出我的结果图：

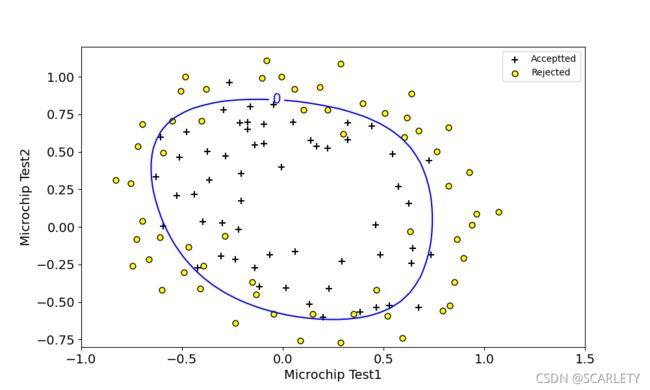
• lambda=1

与题目中参考边界基本一致。

• lambda=0 

 这里与我们发现并没有过拟合，这也许是因为我们使用的是批梯度下降法，寻找到局部最小值的原因，如果使用更高级的算法，我相信会产生过拟合现象。

• lambda=100

这里我们发现，结果明显是欠拟合的。 

三、附录(完整python程序)

如果需要复现,请把这些文件和ex2data1.txt和ex2data2.txt放在一个文件夹内

• main.py

# -*- coding: utf-8 -*-
import numpy as np
from feature_mapping import MapFeature
from gradient import GradientDecent        #用于ex2data1
from gradient_reg import GradientDecentReg #用于ex2data2
from plotdata import PlotData


filename = "ex2data2.txt"
plot = PlotData(filename)
x, y = plot.get_data()
m = MapFeature(x,6)
X = m.mapping_ver2()#这里的特征映射是第二种方式，与第一种的区别在于特征多项式的排列顺序不同，因此对应theta的排列顺序也不一样
if filename == "ex2data2.txt":
    plot.plot_training_data("Training_Data2.png")
    for k in [0, 1, 100]:
        gd = GradientDecentReg(X, y, lamda=k)
        j = gd.cost_func()
        theta = gd.optmize_theta()
     #参考最优theta（用scipy.optmize中的优化函数得到的结果）,这里的theta对应的特征映射是mapping_ver2
      #  theta = np.array([ 1.27273981,  1.18108974, -1.43166669, -0.17513036, -1.19281478,
      # -0.45635758, -0.9246528 ,  0.62527237, -0.9174247 , -0.35723884,
      # -0.27470605, -0.29537769, -0.14388711, -2.0199599 , -0.36553508,
      # -0.61555685, -0.27778507, -0.32738029,  0.12400668, -0.05098942,
      # -0.04473108,  0.01556645, -1.45815829, -0.20600596, -0.29243192,
      # -0.24218804,  0.02777165, -1.04320421])
        if gd.lamda == 0:
            plot.plot_training_data("Training_Data2(lamda=0).png",theta,deci_boundary=True)
        if gd.lamda == 1:
            plot.plot_training_data("Training_Data2(lamda=1).png", theta,deci_boundary=True)
        if gd.lamda == 100:
            plot.plot_training_data("Training_Data2(lamda=100).png", theta,deci_boundary=True)

if filename == "ex2data1.txt":
    gd = GradientDecent(x, y)
    j = gd.cost_func()
    theta = gd.optmize_theta()
    theta = np.array([theta[0][0],theta[0][1],theta[0][2]],np.float32)
    #theta = np.array([-25.16227358,0.20623923,0.20147921], np.float32)#参考theta
    plot.plot_training_data("Training_Data1.png")
    plot.plot_training_data("Training_Data1_DB.png", theta,deci_boundary=True)

• plotdata.py

import numpy as np
import matplotlib.pyplot as plt
from feature_mapping import MapFeature

class PlotData():
    def __init__(self, filename="ex2data1.txt"):
        self.filename = filename

    def get_data(self):
        '''获得特征矩阵和真实值矩阵'''
        with open(self.filename, 'r') as fob:
            contents = fob.readlines()
            nums_comma = contents[0].count(",")#获取逗号数量
            nums_data = len(contents)          #获取数据维度
            x = np.zeros((nums_comma, nums_data), np.float32)
            y = np.zeros((1, nums_data), np.float32)
            for i in range(nums_data):
                l = [j for j in contents[i].split(",")]  # .split()函数分割数据,将以逗号分隔的数据储存在l列表中
                for w in range(nums_comma):               #前面nums_comma个数据是特征
                    x[w][i] = l[w]
                y[0][i] = l[nums_comma].replace("\n", "") #最后一个是结果真实值
        if __name__ == "__main__":#文件内运行用于测试
            print(contents)
            print(x)
            print(y)
        return x, y

    def plot_training_data(self, figname="TrainingData.png", theta= None,deci_boundary = False):
        '''可视化训练集并绘制决策边界，需要给出保存图片的名称和训练好的系数矩阵theta，deci_boundary决定是否绘制决策边界'''
        x, y = self.get_data()
        figure1 = plt.figure(figsize=(10, 6))

        for i in range(len(y[0])):
            if y[0][i] == 1:
                f1 = plt.scatter(x[0][i], x[1][i], marker='+', c="black", label="Admitted", s=50)
            else:
                f2 = plt.scatter(x[0][i], x[1][i], marker='o', c="yellow", edgecolor="black", label="Not admitted",
                                 s=40)
        if self.filename == "ex2data2.txt":
            plt.xlabel("Microchip Test1", fontsize=14)
            plt.ylabel("Microchip Test2", fontsize=14)
            plt.tick_params(axis='both', which='major', labelsize=14)
            plt.ylim((-0.8, 1.2))
            plt.xlim((-1, 1.5))
            if deci_boundary == True:
                '''绘制决策边界'''
                u = np.linspace(-1, 1.5, 50)
                v = np.linspace(-1, 1.5, 50)
                Z = np.zeros((50, 50), np.float32)
                for i in range(len(u)):
                    for j in range(len(v)):
                        u_match = np.tile(u[i], (1, 1))
                        v_match = np.tile(v[j], (1, 1))
                        u_v = np.append(u_match, v_match, axis=0)
                        m = MapFeature(u_v)
                        u_v_mapped = m.mapping_ver2()
                        z = np.vdot(theta, u_v_mapped)
                        Z[j][i] = z        #注意U，V的排列顺序Z要与之完全对应
                U, V = np.meshgrid(u, v)
                f3 = plt.contour(U, V, Z, [0],colors="blue")  # 绘制高度为0的等高线
                plt.clabel(f3, inline=True, fontsize=15)
            plt.legend(handles=[f1, f2], labels=["Acceptted", "Rejected"],loc="upper right")
        if self.filename == "ex2data1.txt":
            plt.xlabel("Exam1 Score", fontsize=14)
            plt.ylabel("Exam2 Score", fontsize=14)
            plt.tick_params(axis='both', which='major', labelsize=14)
            plt.xlim((30, 101))
            plt.ylim((30, 101))
            ticks = np.linspace(30, 100, 8)
            plt.xticks(ticks)
            plt.yticks(ticks)
            if deci_boundary == True:
                '''绘制决策边界'''
                u = np.array([min(x[1]) - 2, max(x[1]) + 2])
                v = (theta[0] + theta[1] * u) / (-theta[2])
                f3, = plt.plot(u, v, linewidth=1, c="blue", label="DecisionBoundary")
                plt.legend(handles=[f1, f2, f3], loc="upper right")
            else:
                plt.legend(handles=[f1, f2], loc="upper right")
        plt.savefig(figname)
        plt.show()

• gradient.py

import matplotlib.pyplot as plt
import numpy as np
#from plotdata import PlotData


class GradientDecent():
    '''梯度下降法'''
    def __init__(self,x,y,alpha = 0.004,iters =400000,lamda = None):
        '''需要给出特征矩阵x和真实值矩阵y，批梯度下降法收敛速度较慢10w次迭代后才开始慢慢收敛，对学习率的要求也很高，默认选择alpha = 0.004，iters = 400000，lamda为正则化参数'''
        self.alpha = alpha
        self.iters = iters
        self.lamda = lamda
        self.x = x
        self.y = y
        self.m = len(x[0])
        self.X = np.append(np.ones((1,self.m),np.float32),self.x,axis = 0)   #按列方向添加
        self.nums_theta = len(self.X)
        self.theta = np.zeros((1,self.nums_theta),np.float32)

    @staticmethod
    def sigmoid(X):
        '''Sigmoid函数，需要一个数组参数X'''
        g = 1/(1+np.exp(-X))   #X可以是数组，返回一个对应维数的结果数组
        return g

    def cost_func(self):
        '''计算代价函数'''

        h_theta = self.sigmoid(np.dot(self.theta,self.X))
        #避免np.log计算值过大采用np.log(data + 1e-5)来避免产生inf项
        J_theta = (np.vdot(self.y,np.log(h_theta+1e-5).T) + np.vdot((1-self.y),np.log(1-h_theta +1e-5).T))/(-self.m)
        return h_theta,J_theta

    def optmize_theta(self):
        '''最优化theta'''
        J = []  #储存每一步迭代的代价值用来观察迭代过程
        for i in range(self.iters):
            h,j = self.cost_func()
            J.append(j)
            partial_theta = np.dot((h-self.y),self.X.T)/self.m
            self.theta = self.theta - self.alpha*partial_theta
        if __name__ == "__main__":
            print(h)
            print(j)
            print(self.theta)
            x_iter = np.arange(0,400000)
            y_J = np.array(J)
            plt.plot(x_iter,y_J,linewidth = 1)
            plt.show()
        return self.theta






#if __name__ =="__main__":
#    filename = "ex2data1.txt"
#    p = PlotData(filename)
#    x,y = p.get_data()
#    gd = GradientDecent(x,y)
#    j = gd.cost_func()
#    theta = gd.optmize_theta()
#    x_pred = np.array([1,45,85])
#    h = gd.sigmoid(np.vdot(theta,x_pred.T))
#    print(h)

• evaluate_logistic_reg.py

import numpy as np
from plotdata import PlotData
from gradient import GradientDecent

p = PlotData()
x,y = p.get_data()
g = GradientDecent(x,y)
theta = np.array([-24.293768,0.19929314,0.19445102])
X = np.append(np.ones((1,len(x[0])),np.float32),x,axis=0)
h_theta = g.sigmoid(np.dot(theta,X))
for i in range(len(h_theta)):   #选择0.5作为阈值来进行分类
    if h_theta[i] >= 0.5:
        h_theta[i] = 1
    else:
        h_theta[i] = 0
y_compare = y - h_theta         #真实值与预测值做差
ground_truth_0 = y[0].tolist().count(0)#真实值为0的个数
ground_truth_1 = y[0].tolist().count(1)#真实值为1的个数
ans_right = y_compare[0].tolist().count(0) #为0的个数即为正确预测的个数
ans_wrong_0 = y_compare[0].tolist().count(-1) #为-1的个数即为0类预测失败的个数
ans_wrong_1 = y_compare[0].tolist().count(1) #为1的个数即为1类预测失败的个数
correct_rate_0 = (ground_truth_0-ans_wrong_0)/ground_truth_0
correct_rate_1 = (ground_truth_1-ans_wrong_1)/ground_truth_1
correct_rate = ans_right/len(y[0])
print("Admitted（1）: " + str(ground_truth_1))
print("NotAdmitted（0）: " + str(ground_truth_0))
print("Admitted（pred）: " + str(ground_truth_1-ans_wrong_1))
print("NotAdmitted（pred）: " + str(ground_truth_0-ans_wrong_0))
print("1_correct_rate: " + str(correct_rate_0*100) + "%")
print("0_correct_rate: " + str(correct_rate_1*100) + "%")
print("Total_correct_rate: " + str(correct_rate*100) + "%")

• feature_mapping.py

import numpy as np

class MapFeature():
    '''将初始特征矩阵映射到高阶多项式特征矩阵'''
    def __init__(self,x,degree:int = 6):
        '''给定初始特征矩阵x，和多项式的最高阶数degree'''
        self.x = x
        self.m =len(self.x[0])#获取特征的维数
        self.degree = degree

    def mapping_ver1(self):
        '''这是第一种映射方法'''
        X = np.append(np.ones((1,self.m),np.float32),self.x,axis=0) #按列添加
        if self.degree >= 2:
            for i in range(2,self.degree+1):
                for j in range(i+1):
                    x_mapping = np.multiply(np.power(self.x[0],i-j),np.power(self.x[1],j))#x_mapping 是118维向量,np.multiply()是矩阵对应元素相乘，np.dot()是矩阵乘法
                    x_mapping_match = np.tile(x_mapping,(1,1))            #将x_mapping变成1*118的矩阵与X维数相匹配
                    X = np.append(X,x_mapping_match,axis=0)  #axis=0表示按列方向（也就是垂直方向添加）
        x_mapped = X
        return x_mapped

    def mapping_ver2(self):
        '''这是另一种映射方法'''
        X = np.ones((1,self.m))
        for i in range(self.degree+1):
            for j in range(self.degree-i+1):
                x_mapping = np.multiply(np.power(self.x[0], i), np.power(self.x[1],j))  # x_mapping 是118维向量,np.multiply()是矩阵对应元素相乘，np.dot()是矩阵乘法
                x_mapping_match = np.tile(x_mapping, (1, 1))  # 将x_mapping变成1*118的矩阵与X维数相匹配
                X = np.append(X, x_mapping_match, axis=0)
        X = np.delete(X,0,axis=0) #删除第一行
        x_mapped = X
        return x_mapped

#if __name__ == "__main__":#下面的代码是本文件内用于测试得到作用
#    p = PlotData(filename="ex2data2.txt")
#    x,y = p.get_data()
#    m = MapFeature(x,6)
#    X = m.mapping_ver2()
#    print(X)
#    print(type(X),X.shape)

• gradient_reg.py

import matplotlib.pyplot as plt
import numpy as np
#from feature_mapping import MapFeature

class GradientDecentReg():
    '''梯度下降法'''
    def __init__(self,x,y,alpha = 0.1,iters =4000,lamda = 1):
        '''需要给出映射后的特征矩阵x和真实值矩阵y，默认选择alpha = 0.1，iters = 3000，lamda为正则化参数'''
        self.alpha = alpha
        self.iters = iters
        self.lamda = lamda
        self.x = x
        self.y = y
        self.m = len(x[0])
        self.X = x
        self.nums_theta = len(self.X)
        self.theta = np.zeros((1,self.nums_theta),np.float32)

    @staticmethod
    def sigmoid(X):
        '''Sigmoid函数，需要一个数组参数X'''
        g = 1/(1+np.exp(-X))   #X可以是数组，返回一个对应维数的结果数组
        return g

    def cost_func(self):
        '''计算代价函数'''
        h_theta = self.sigmoid(np.dot(self.theta,self.X))
        theta_reg = self.theta[0][1:].copy()     #theta0不需要正则化
        j_reg = (self.lamda * (np.vdot(theta_reg, theta_reg.T))) / (2 * self.m)   #正则化惩罚项
        J_theta = j_reg + (np.vdot(self.y,np.log(h_theta+1e-5).T) + np.vdot((1-self.y),np.log(1-h_theta +1e-5).T))/(-self.m) #避免np.log计算值过大np.log(data + 1e-5)
        return h_theta,J_theta
    def optmize_theta(self):
        '''用批梯度下降法最优化theta'''
        J = []#用于储存每一步迭代计算的代价函数值
        for i in range(self.iters):
            h,j = self.cost_func()
            J.append(j)
            theta_modified = self.theta.copy()
            theta_modified[0][0] = 0     #为了实现theta0不参与正则化
            partial_theta = np.dot((h-self.y),self.X.T)/self.m + self.lamda*theta_modified/self.m
            self.theta = self.theta - self.alpha*partial_theta
        if __name__ == "__main__":
            '''绘制每一步迭代的代价与迭代次数的曲线，用来观察迭代过程'''
            print(h)
            print(J)
            print(self.theta)
            x_iter = np.arange(0,self.iters)
            y_J = np.array(J)
            plt.plot(x_iter,y_J,linewidth = 1)
            plt.show()
        return self.theta

#if __name__ =="__main__":#文件内用于测试的的代码
#    filename = "ex2data2.txt"
#    p = PlotData(filename)
#    x,y = p.get_data()
#    mf = MapFeature(x)
#    X = mf.mapping_ver2()
#    gd = GradientDecent(X,y)
#    j = gd.cost_func()
#    theta = gd.optmize_theta()

四、参考资料

• 吴恩达2014年机器学习课程
• 黄海广博士机器学习个人笔记
• 黄海广博士机器学习编程作业