matlab之画图

目录

1. 横纵坐标轴

2. 格点显示

3. 图、窗体Figure1的命名

4. 多个图形叠加绘制

5. 频谱图

 5.1 已知信号画频谱图

 5.2 已知传输函数画频谱图

---

1. 横纵坐标轴

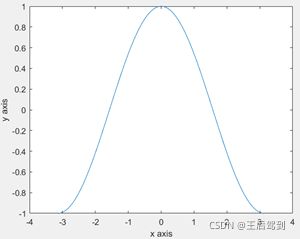
        横纵坐标轴标签：

x = -pi: 0.01: pi;
figure, plot(x, cos(x));
xlabel(“x axis”);
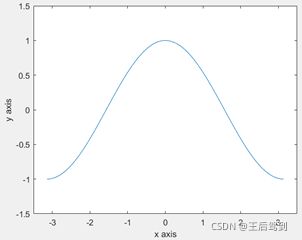
ylabel(“y axis”);

         横纵坐标轴范围自定义:

xlim([-3.5 3.5]);
ylim([-1.5 1.5]);

 

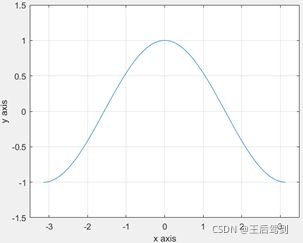
2. 格点显示

        默认情况下，用figure和plot指令画完的图，并没有格点显示，这样，在有时候想要仔细观测信号幅度时不太方便，可以通过指令：grid on; 来显示格点。

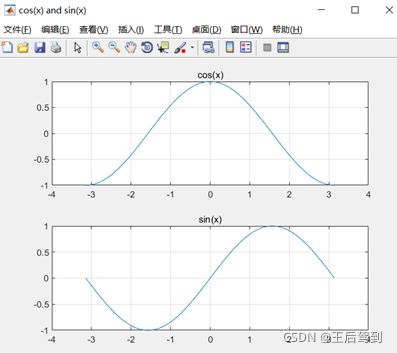
3. 图、窗体Figure1的命名

figure('NumberTitle','off','Name','cos(x) and sin(x)'); 
subplot(2,1,1), plot(x, cos(x)); grid on; title("cos(x)");
subplot(2,1,2), plot(x, sin(x)); grid on; title("sin(x)");

4. 多个图形叠加绘制

        多个图形叠加绘制，可以在plot之后，通过hold on; 来解决。并采用legend给各图形追加标签说明。

        参考代码如下：

x = -pi: 0.01: pi;
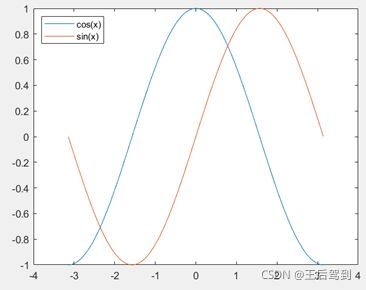
figure, plot(x, cos(x)); hold on; plot(x, sin(x));
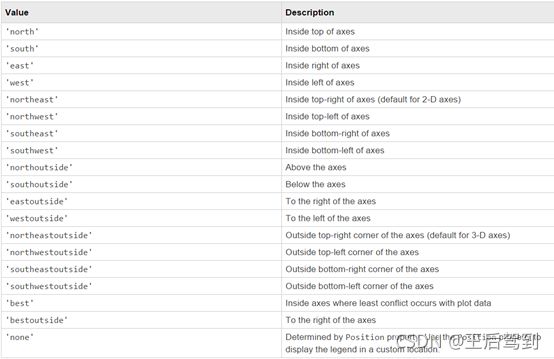
legend("cos(x)","sin(x)",'Location','northwest');

        其中，各图形的标签可以放在不同位置，通过对标签位置的调节，可以避免标签对图形可能的遮挡。标签位置支持以下几种：

        绘制后的效果图如下： 

5. 频谱图

 5.1 已知信号画频谱图

        在已知信号的情况下，画频谱图有两种方法，一种是使用pwelch，另一种是使用fvtool。

        参考代码如下：

Fs    = 25e6;
Ts    = 1/Fs;
Fsin6 = 6e6;
data_len  = 1000;
t = ([1:1:data_len]-1) * Ts;
x = real(exp(sqrt(-1)*2*pi*Fsin6*t));
window  = 500;
overlap = 300;
nfft    = 500;
[y,f] = pwelch(x,window,overlap,nfft,Fs);
figure('NumberTitle','off','Name','pwelch'); 
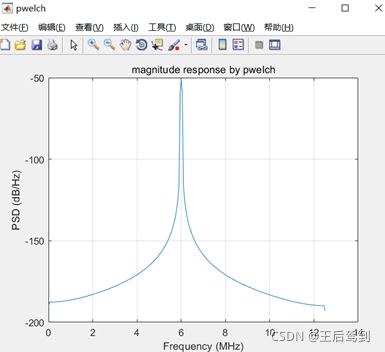
plot(f/1e6, 10*log10(y)), xlabel("Frequency (MHz)"), ylabel("PSD (dB/Hz)"), 
grid on, title("magnitude response by pwelch");
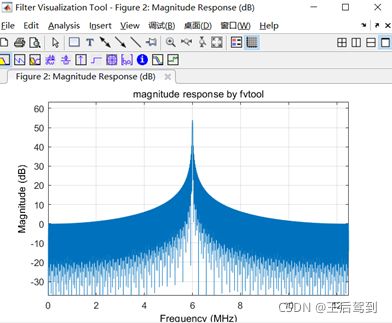
fvtool(x,'Fs',Fs,'Color','white'); title('magnitude response by fvtool');

        得到频谱图如下：

        这两种画频谱图的方法都非常好用，但这两种方法画出来的频谱图会有略微差距。而至于为什么会有这样的差别，哪种更接近真实情况，没有调查过，不得而知了。。。

 5.2 已知传输函数画频谱图

        在已知传输函数的情况下，画频谱图也有两种方法，一种是使用freqz，另一种是使用fvtool。

        参考代码如下：

Fs    = 25e6;
alpha = 0.9992;
beta  = 0.8763;
b = [1 -2 * beta           1] * (1 + alpha) / 2;
a = [1 -beta * (1 + alpha) alpha];
n = 500;
freqz(b, a, n, Fs); title('magnitude response by freqz');
fvtool(b,a,'Fs',Fs,'Color','white'); title('magnitude response by fvtool');

        得到频谱图如下：