写在前边
这篇文章呢,我们接着聊一下排序算法,我们之前已经谈到了简单插入排序 和ta的优化版希尔排序 ,这节我们要接触一个更“高级”的算法了--快速排序。
在做洛谷的时候,遇到了一道卡优化的题,如果没有去对快排进行优化的话,会有几个点是TLE的,后边我们可以围绕这道题来做各种优化,先来认识一下快速排序。
思路
假如我们的计算机每秒钟可以运行 10 亿次,那么对 1 亿个数进行排序,桶排序只需要 0.1 秒,而冒泡排序则需要 1 千万秒,达到 115 天之久,是不是很吓人?那有没有既不浪费空间又可以快一点的排序算法呢?那就是“快速排序”!
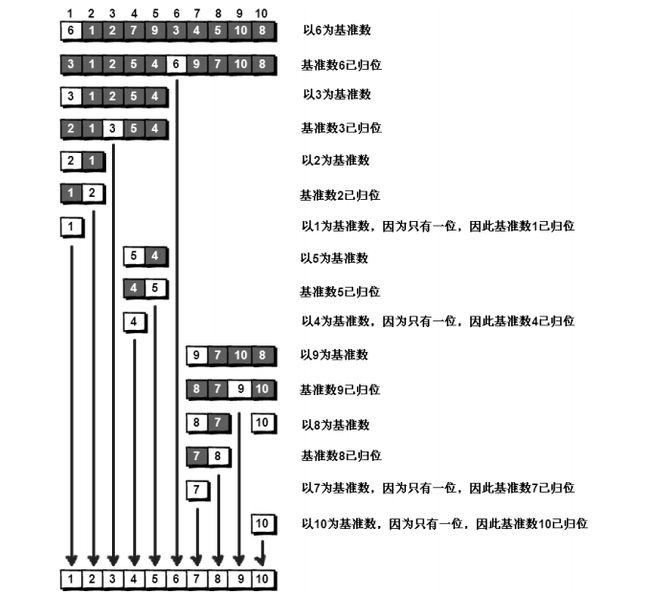
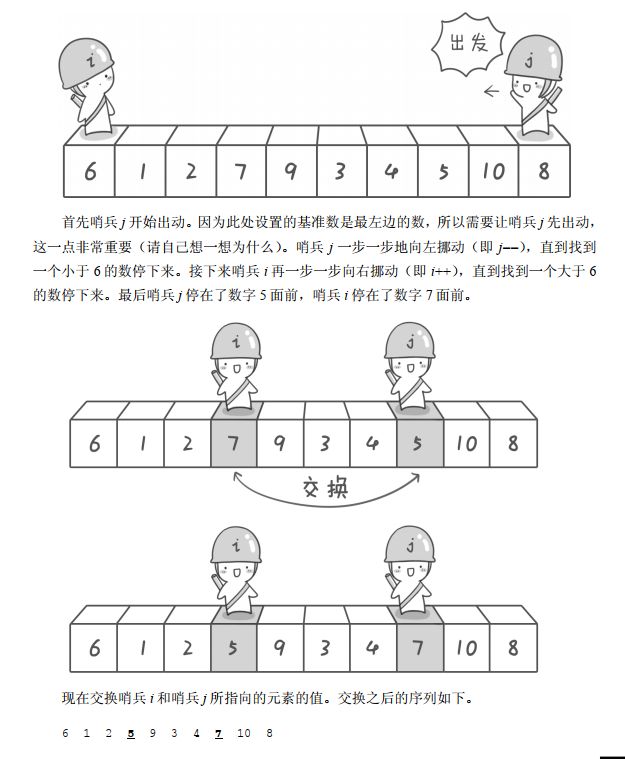
假设我们现在对“** 6 1 2 7 9 3 4 5 10 8”这 10 个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,这就是一个用来参照的数,待会儿你就知道它用来做啥了)。为了方便,就让第一个数 6 作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在 6 的右边,比基准数小的数放在 6 的左边**,类似下面这种排列。
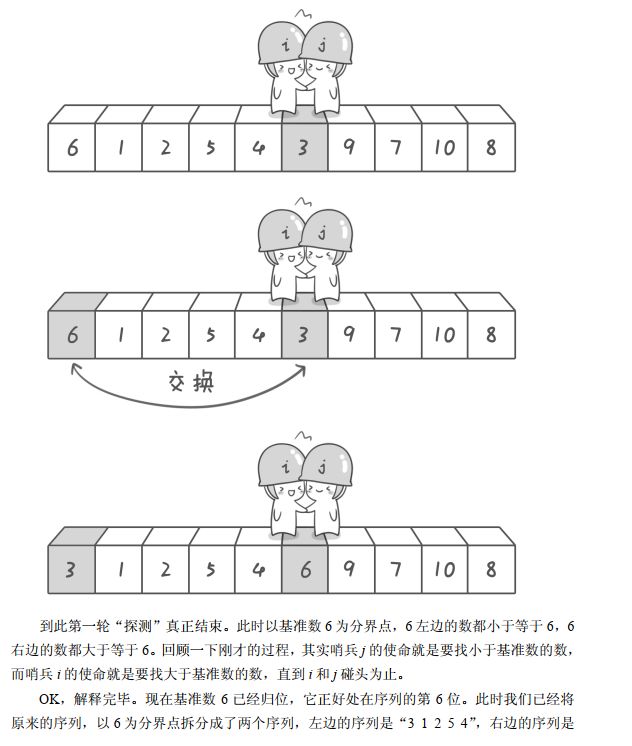
3 1 2 5 4 6 9 7 10 8
在初始状态下,数字 6 在序列的第 1 位。我们的目标是将 6 挪到序列中间的某个位置,假设这个位置是 k。现在就需要寻找这个 k,并且以第 k 位为分界点,左边的数都小于等于 6,右边的数都大于等于 6。
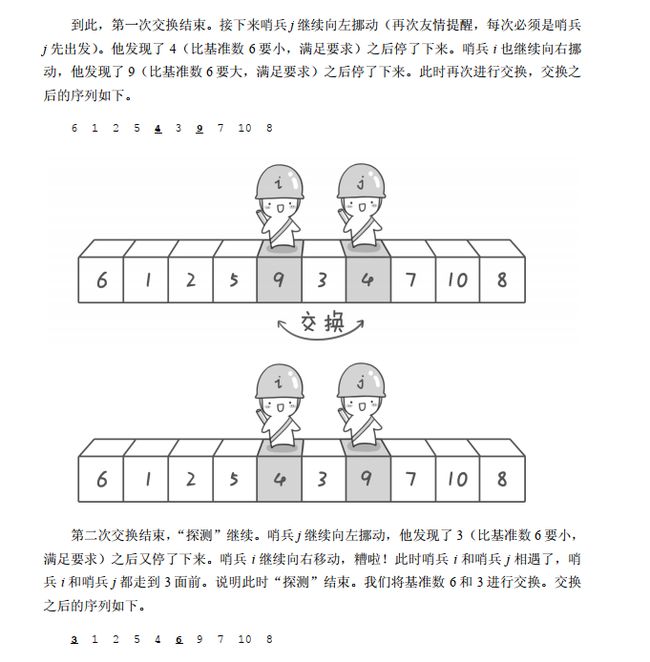
方法其实很简单:分别从初始序列“ 6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于 6 的数,再从左往右找一个大于 6 的数,然后交换它们。这里可以用两个变量 i 和 j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵 i”和“哨兵 j”。刚开始的时候让哨兵 i 指向序列的最左边(即 i=1),指向数字 6。让哨兵 j 指向序列的最右边(即 j=10),指向数字 8。
图源: 《啊哈算法》
完整流程图
如果mid取最左端的话,当本身有序时,会沦为冒泡排序,变成n平方
(例题)洛谷1177快速排序
https://www.luogu.com.cn/problem/P1177
错误版本
无优化,有序会TLE
#include
#include
int a[1000001];//定义全局变量,这两个变量需要在子函数中使用
void swap(int* a, int* b) {
int temp;
temp = *a;
*a = *b;
*b = temp;
}
//递归方法
void quicksort(int left, int right) {
//举例子可得出若左边大于等于右边就返回?
//大于的情况是:index刚好==right,然后还要再去(index+1,right)
if (left >= right) {
return;
}
//默认基准index是最左边那个,且i从左边开始,j从右边开始
int i = left, j = right, index = left;
//重构方法
//大前提,两个没相遇
while (i != j) {
//里边还得判断一下i= a[left]&&i 先取到mid,然后让左边跟mid交换
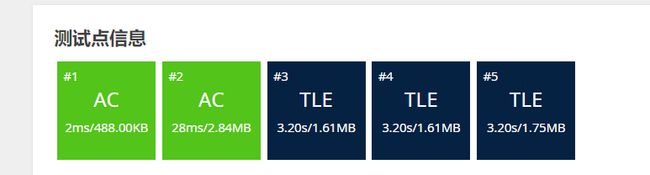
由于是单边搜索,后两个点都TLE
#include
#include
#include
#include
#include
#include
void swap(int arr[], int i, int j)
{
int temp;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
void QuickSort(int arr[], int left, int right)
{
int i, pivot;
if (left >= right)
return;
pivot = left;
swap(arr, left, (left + right) / 2);
for (i = left + 1; i <= right; i++) //单边搜索,可以该为双向搜索
if (arr[i] < arr[left])
swap(arr, i, ++pivot);
swap(arr, left, pivot);
QuickSort(arr, left, pivot - 1);
QuickSort(arr, pivot + 1, right);
}
int main()
{
int n;
int *arr;
int i;
scanf("%d", &n);
arr = (int*)malloc(sizeof(int) * (n + 1));
for (i = 1; i <= n; i++)
scanf("%d", arr + i);
QuickSort(arr, 1, n);
for (i = 1; i <= n; i++)
printf("%d ", arr[i]);
return 0;
}
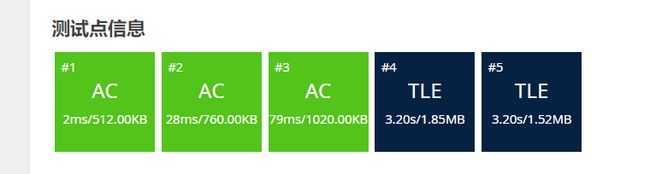
改进成双边搜索
只是最后一个点TLE了,而最后一个点,刚好就是常数列的情况
#include
#include
int a[100010];//定义全局变量,这两个变量需要在子函数中使用
void swap(int* a, int* b) {
int temp;
temp = *a;
*a = *b;
*b = temp;
}
//递归方法
void quickSort(int left, int right) {
//举例子可得出若左边大于等于右边就返回?
//大于的情况是:index刚好==right,然后还要再去(index+1,right)
if (left >= right) {
return;
}
//默认基准index是最左边那个,且i从左边开始,j从右边开始
int i = left, j = right, index ;
int mid=(left+right)/2;
swap(&a[left],&a[mid]);
index=left;
//重构方法
//大前提,两个没相遇
while (i != j) {
//里边还得判断一下i= a[left]&&i 复盘mid(考虑常数列)
还没三数取中,取到的mid是最小的话还是会退化到冒泡n平方
#include
#include
using namespace std;
int a[100010];
//交换元素位置
void swap(int* a, int* b) {
int temp;
temp = *a;
*a = *b;
*b = temp;
}
void quickSort(int* arr, int low, int high) {
//若长度已经不符合要求,直接返回
if (low >= high) {
return;
}
int left = low;
int right = high;
//选取中间为基准,注意是取中间的值,而不是下标,因为下标可能在后续交换中会改变
//比如left走到了mid这里,而right停在了mid右边,这时会去交换,arr[mid]就变了
int mid = arr[(low + high) >> 1];
while (left <= right) {
//注意是小于,如果是小于等于的话,常数列就会一直left移动,而right不移动,沦为n平方
while (arr[left] < mid) {
left++;
}
//同样注意是大于
while (arr[right] > mid) {
right--;
}
//这里要注意是小于或等于,以便于left和right直接跳到枢纽点的左右
if (left <= right) {
swap(&arr[left], &arr[right]);
left++;
right--;
}
}
//递归调用
//right走到了区间一的尾部
quickSort(arr,low, right);
//left走到了区间二的头部
quickSort(arr, left, high);
}
int main()
{
int n, i;
cin >> n;
for (i = 1; i <= n; i++)
{
cin >> a[i];
}
quickSort(a,1,n);
for (i = 1; i <= n; i++)
{
cout << a[i] << " ";
}
cout << endl;
}
流程图
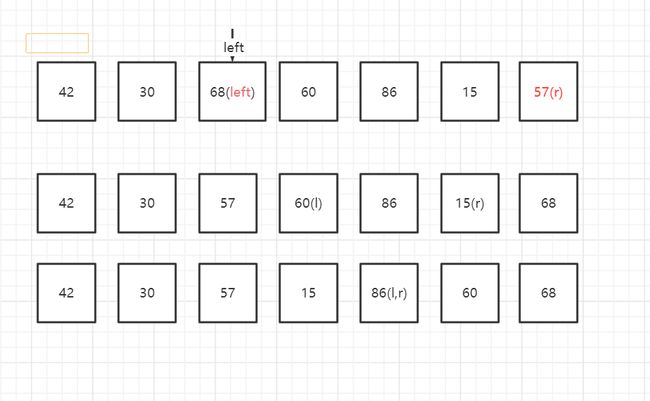
此处取到的mid是60
此时left和right已经相遇了
- 然后left发现不满足条件,86>mid(60),left还在86
- right满足条件,right去--,走到了15那里停下来
- 然后left不满足<=right,直接就要开始继续递归了
- 递归的区间①是: [42,15] (都小于等于60)
- 区间②是 : [86,68] (都大于等于60)
while (arr[left] < mid) {
left++;
}
//同样注意是大于
while (arr[right] > mid) {
right--;
}
//这里要注意是小于或等于,以便于left和right直接跳到枢纽点的左右
if (left <= right) {
swap(&arr[left], &arr[right]);
left++;
right--;
}
//递归调用
//right走到了区间一的尾部
quickSort(arr,low, right);
//left走到了区间二的头部
quickSort(arr, left, high);
问题
因为没有去把枢纽放到正确的位置,导致最后其实分出来的区间长度会多出一个元素:枢轴(这样会很影响时间效率吗)
自行用一定数据量测试的话,时间效率上差距还算不上很大的。
**结合三数取中(暂时的神)
#include
#include
#include"RcdSqList.h"
using namespace std;
//int a[100010];
//交换元素位置
void swap(int* a, int* b) {
int temp;
temp = *a;
*a = *b;
*b = temp;
}
//三数取中
int getmid(int* array, int left, int right)
{
int mid = left + ((right - left) >> 1);
if (array[left] <= array[right])
{
if (array[mid] < array[left])
return left;
else if (array[mid] > array[right])
return right;
else
return mid;
}
else
{
if (array[mid] < array[right])
return right;
else if (array[mid] > array[left])
return left;
else
return mid;
}
}
void quickSort(int* arr, int low, int high) {
//若长度已经不符合要求,直接返回
if (low >= high) {
return;
}
int left = low;
int right = high;
//选取中间为基准,注意是取中间的值,而不是下标,因为下标可能在后续交换中会改变
//比如left走到了mid这里,而right停在了mid右边,这时会去交换,arr[mid]就变了
//调用三数取中,得到中间数
int mid = arr[getmid(arr, low, high)];
while (left <= right) {
//注意是小于,如果是小于等于的话,常数列就会一直left移动,而right不移动,沦为n平方
while (arr[left] < mid) {
left++;
}
//同样注意是大于
while (arr[right] > mid) {
right--;
}
//这里要注意是小于或等于,以便于left和right直接跳到枢纽点的左右
if (left <= right) {
swap(&arr[left], &arr[right]);
left++;
right--;
}
}
//递归调用
//right走到了区间一的尾部
quickSort(arr, low, right);
//left走到了区间二的头部
quickSort(arr, left, high);
}
int main()
{
int n, i;
/*cin >> n;*/
/*for (i = 1; i <= n; i++)
{
cin >> a[i];
}*/
int a[100] = { 0,42 ,90,30,86,42,15,57,20 };
quickSort(a, 1, 8);
for (i = 1; i <= 8; i++)
{
cout << a[i] << " ";
}
cout << endl;
}
总结
最后是下载了测试点,然后看了博客,去找超时的原因,其实是完全有序
然后拿标准答案debug一下,终于发现了区别,就是常数列的时候他两个都移动,我只是一个移动,就退化成n平方了
注意
要<号而不是<=
**要去放大问题,比如j一直往左走,要放大到一直走走走走到i那里去了!
看黑马视频得出的感悟....
这个问题很严重,会变成n平方
如果把基准放最左边,而本身有序的话就会超时了
xxxx枢轴要选大小为中间的值,才能解决完全有序的情况(得三数取中.)
- 注意这里的取中间值不是说取区间中间的值,而是大小在首尾和区间中间数三个值排列居中的那个
- 如果取的是区间中间的值,并不能解决完全有序的问题,比如 5 4 1 2 3 ,取mid等于1,又是取到了最小的情况,最后mid放到正确的位置(即第一个位置),递归他的左右,并没有起到把原区间化成两半的效果,只是得到了右边那一段,相当与只是减少了一个元素(类似冒泡的把一个元素放到正确的位置而已)
让left++的条件应该是<号! , 交换完要顺便让left++,right--,这样才能解决常数列的情况
如果我们不在交换完做移动的话,那>就得改成>=,这样才会移动,但就变成单指针移动了,还是退化成n平方了
交换完移动后,left和right刚好就是两个区间的首跟尾
**三向切割法
https://www.luogu.com.cn/problem/P1177(依旧是模板题)
先来看代码
#include
#include
using namespace std;
int a[100010];
//交换元素位置
void swap(int* a, int* b) {
int temp;
temp = *a;
*a = *b;
*b = temp;
}
//三数取中
int getmid(int* array, int left, int right)
{
int mid = left + ((right - left) >> 1);
if (array[left] <= array[right])
{
if (array[mid] < array[left])
return left;
else if (array[mid] > array[right])
return right;
else
return mid;
}
else
{
if (array[mid] < array[right])
return right;
else if (array[mid] > array[left])
return left;
else
return mid;
}
}
void quickSort_2(int rcd[], int low, int high) {
if (low >= high) {
return;
}
//调用三数取中,获取枢纽位置
int pivot=getmid(rcd,low,high);
//把枢纽值放到low位置(交换)
swap(&rcd[low],&rcd[pivot]);
//枢纽值就等于rcd[low]
int pivotVal = rcd[low];
//i用来遍历一趟区间
int left, right, i;
//直接从枢纽的下一位开始遍历区间
left = low, right = high, i = low + 1;
//遍历整个区间
while (i <= right) {
//若小于枢纽值
if (rcd[i] < pivotVal) {
//得放到前边,跟left交换
swap(&rcd[i], &rcd[left]);
//交换完,i换来了一个i前边的值,肯定比较过了,所以i++
i++;
//left换来了一个i原来位置的值,也比较过了,所以left++
left++;
}
//若大于枢纽值
else if(rcd[i]>pivotVal)
{
//得放到后边,跟right交换
swap(&rcd[i], &rcd[right]);
//right换来了一个i原来位置的值,也比较过了,所以right++
right--;
//i不动,因为换过来一个i后边的新的值,还没比较过
}
//等于的情况
else
{
i++;
}
}
quickSort_2(rcd, low, left - 1);
quickSort_2(rcd, right + 1, high);
}
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
quickSort_2(a,0, n - 1);
for (int i = 0; i < n; i++) {
i == n - 1 ? printf("%d", a[i]) : printf("%d ", a[i]);
}
}
粗糙的流程图
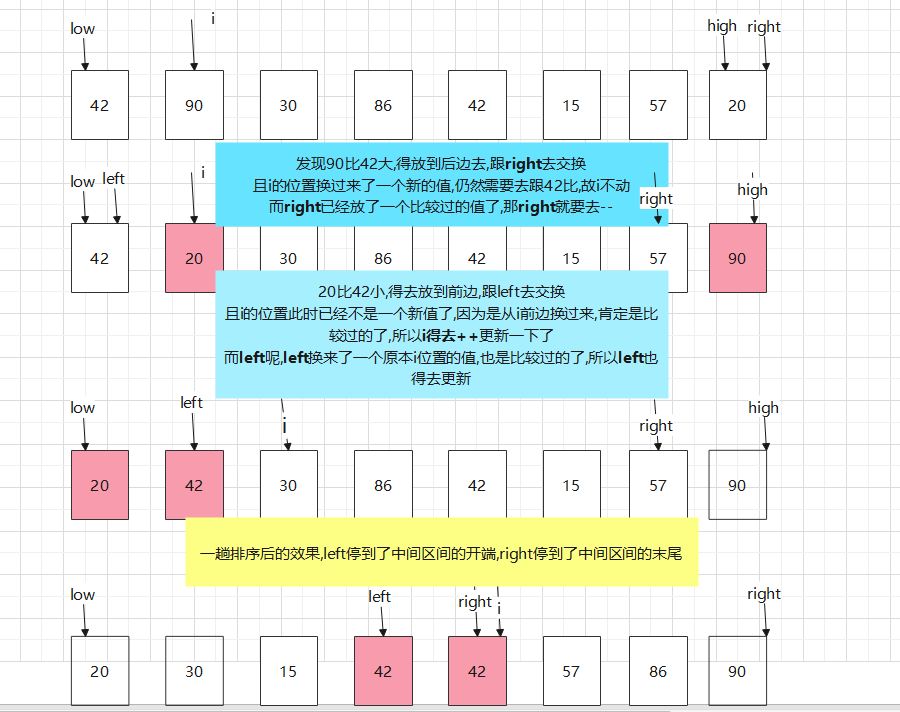
这里我们先默认枢轴就是最左边的元素就好了,方便理解(实际情况再按上边代码取中后跟最左边交换即可)
用一个i去遍历这个区间,还需要一个left和一个right指针
- 当 rcd[i]大于枢纽值时,比如图中的90
- 当rcd[i]小于枢纽值时,比如图中的20
- 当rcd[i]等于枢纽值时,比如图中的42
具体看图中的文字说明
总结一下就是,如果该位置是一个已经跟枢纽值比较过了的值,或者换过来一个已经跟枢纽值比较过了的值(那就需要更新一下他的指针位置)
优势
- 减少了对重复元素的比较操作,因为重复元素在一次排序中就已经作为单独一部分排好了,之后只需要对不等于该重复元素的其他元素进行排序。
写在最后
- 到了快排这里,其实已经涉及到一些递归的知识,跟递归相关的其实还有“折半查找”、“归并排序”等,本专栏也还还会持续更新相关的知识,欢迎关注一起学习!