图解KMP算法原理及其代码分析

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。该算法是字符串两大难点算法之一。在这里我想对提出该算法的三位神人表达我的敬仰之情，真正理解了该算法的奥秘之后，你就会惊叹此算法的思路是多么的巧妙！！！

KMP算法的强大之处不仅仅在于思路的巧妙，更在于代码的简洁！！！

网络上很多种KMP算法的写法，算法思路都一样，个人认为下面这一种是比较好理解的。

本篇文章所讲内容有一定难度，请静下心来体会。相信你一定可以掌握KMP算法的精髓。

在讲解算法原理之前，我们先看看在下面匹配字符串过程中遇到的问题。

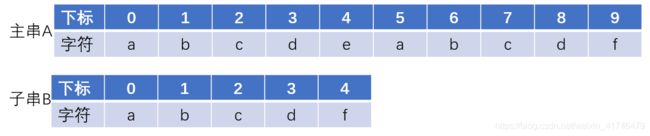
（1）字符串模式匹配问题

我们要在主串中查找与子串完全匹配的部分，如图所示。

 解决方案一：暴力匹配

遇到不相等的情况的时候，就将子串位移一位，再进行比较。这里在主串下标为4的位置不匹配，子串向右位移一位继续匹配。

直到在主串中找到与子串匹配的部分或者是遍历完主串。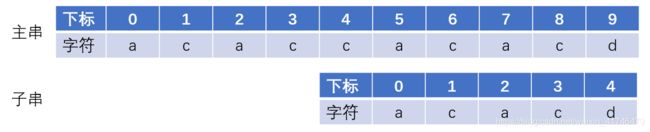显然这种暴力匹配的思路和代码实现确实比较简单，但是我们从时间复杂度的方面来分析一波这种方式的缺点。 最好的情况是一来就匹配成功，时间复杂度O(n)，最坏的情况下末尾匹配成功，时间复杂度O(m*n)。很显然，当主串和子串的长度十分大的时候，暴力匹配算法极其消耗时间。讨论下面两种主要情况。

①情况一：

出现这种情况的时候，我们对失配字符前面的部分分析可得:

A[0] = B[0]        A[1] = B[1]         A[2] = B[2]         A[3] = B[3]        B[0] != B[1] != B[2] != B[3]

联立可得：B[0] != { A[1]，A[2]，A[3] }                    

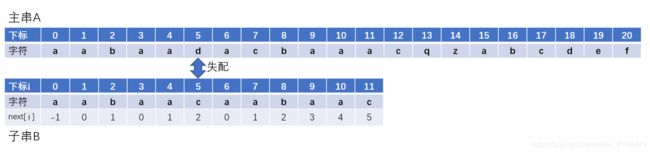
对此情况分析可知我们完全可以避开下图中的1、2、3步，因为我们已经分析得出了B[0] != {A[1]，A[2]，A[3] }的结论。一步到位，直接跳转到第4步所示位置再进行比较。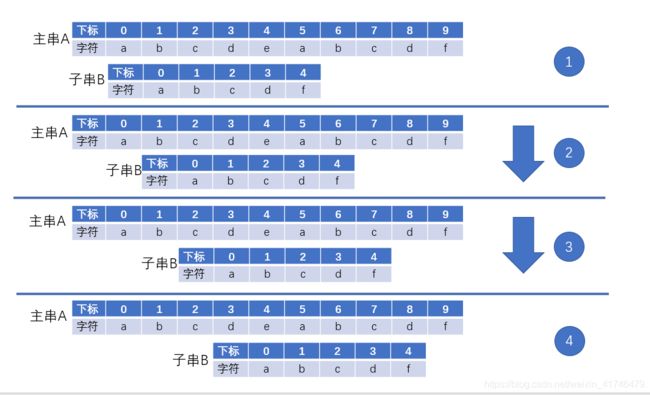

 ②情况二：

 出现这种情况的时候，分析可得：B[0] != B[1]，B[1] = A[1]

可推出：B[0] != A[1]

我们很明显可以发现第1步的比较是多余的，因为我们已经推出了B[0] != A[1]​​​​​​，那么位移一位对B[0]和A[1]比较是不能匹配的。完全可以直接跳至第2步再进行比较。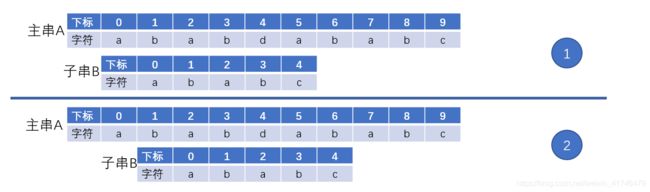

完成了上面的情况分析，我们接下来就可以来解析KMP算法了。

（2）最长相等前后缀的概念：

对于字符串abcabc   

前缀有{ a，ab，abc，abca，abcab } 后缀有{ c，bc，abc，cabc， bcabc } ，比较可知最长相等前后缀为abc。

对于字符串nihaownihao，最长相等前后缀为nihao。现在大致弄明白了最长相等前后缀的意思了吧。最长相等前后缀的长度决定了子串遇到不匹配字符时回溯的位置。

（3）KMP算法匹配原理图解 

 当遇到了失配的字符的时候，我们要移动子串重新匹配。但是我们该怎么移动呢？这个时候最长相等前后缀就发挥了用处。红色部分已匹配部分的字符串相等，那么最长相等前后缀也相同。

子串移动:子串的红色部分最长相等前缀和主串红色部分最长相等后缀对齐。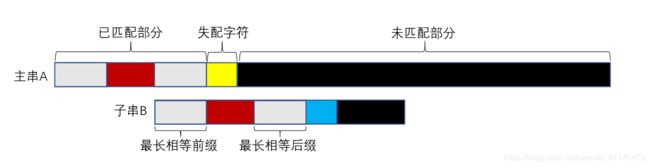

 说到这里KMP算法匹配原理大体方向已经清晰了，但是我们如何用代码来判断遇到不匹配字符时子串回溯的位置呢？其中还有很多细节。（很多情况下我们思考想出的方案，用代码实践写出来往往比较困难，甚至有些细节问题在写代码的时候才会暴露。）这里引入了一个next数组存储子串的最长相等前后缀长度，这个长度的大小也表示该处字符不匹配时应该回溯到的字符的下标。next数组只跟子串有关。next数组记载下标为i的字符前面部分字符串的最长相等前后缀长度。第一个字符我们设置next[0]=-1。

（4）next数组求解原理及匹配样例图解：

举个例子

首先对子串求next数组

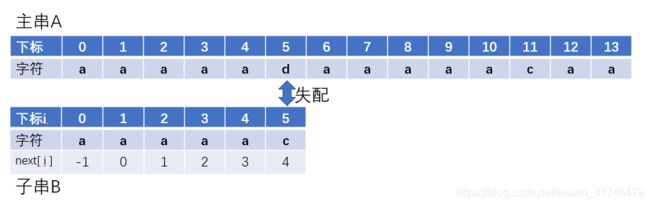
 当我们遇到失配字符的时候，移动子串。观察一下，之下失配位置子串下标为5，next[5]=2，子串回溯到下标为2的位置继续匹配。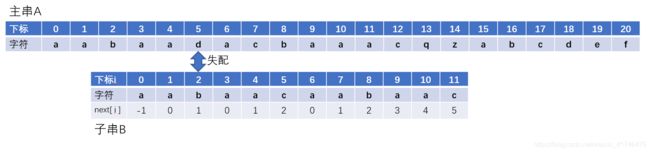接下来两次回溯情况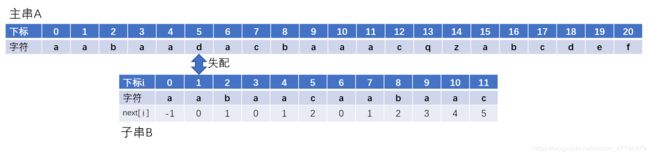

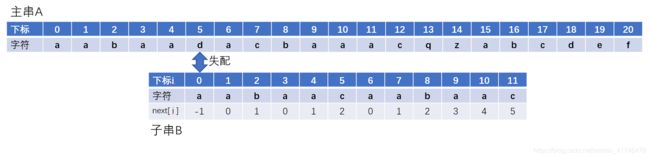
这个时候你肯定会问了，回溯到next[0]=-1了怎么办呢？很简单，下次位移就位移一个单位跳过即可。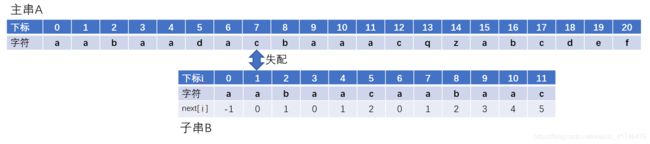 原理了解完毕，我们接下来就可以分析代码了。

（5）求next数组代码分析：

typedef struct strToNext
{	
	char data[MaxSize];
	int length;			//串长
} SN;

void GetNext(SN t,int next[])    //由模式串t求出next值
{

	int j=0,k=-1;
	next[0]=-1;//第一个字符前无字符串，给值-1

	while (j

 可以带入aaaaaaaab和aabaacaabaac这两个字符串体会一下代码中的回溯问题。

（6）求next数组回溯问题分析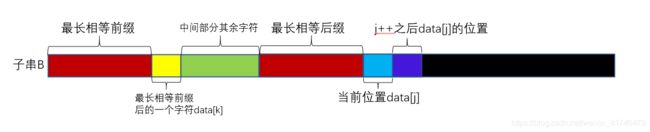：可以很直观的看出如果data[j]=data[k],那么蓝色字符后一个字符在next数组中对应的数值就为最长相等前缀加一（即红色和黄色部分长度之和）。如果data[j]!=data[k]，进行回溯，k=next[k]，此时就相当于把上图红色部分最长前缀后一个字符的下标赋值给k，然后再比较data[j]和data[k]。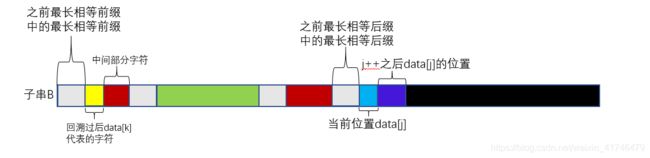

回溯过后再次比较data[j]和data[k]，如果data[j]=data[k]，那么蓝色字符后一个字符在next数组中对应的数值就为最长相等前缀中的最长相等前缀加一（即灰色和黄色部分长度之和）。如果不相等，再次循环此过程。

看到这里有没有一种豁然开朗的感觉！！！next数组解决了，KMP算法就解决了一大半了。

其实，KMP算法还可以再改进一点点。（算法本身已经如此强大了，居然还可以改进？）

举个例子：

 显然这个时候子串前面的所有都不和d匹配，但是KMP算法依旧会回溯到子串下标为4的地方再进行比较。并且还会继续回溯到下标为3，下标为2，下标为1，直到0。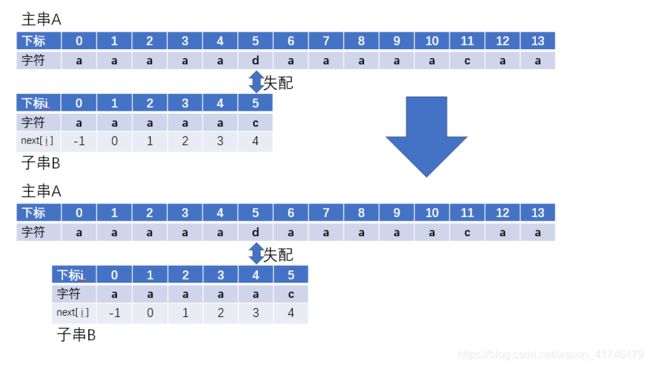（7）求next数组代码改进版本：

typedef struct strToNext
{	
	char data[MaxSize];
	int length;			//串长
} SN;
void GetNext(SN t,int next[])    //由模式串t求出next值
{
	int j=0,k=-1;
	next[0]=-1;//第一个字符前无字符串，给值-1
	while (j

（8）KMP算法主体部分：

int KMPIndex(SN s,SN t)  //KMP算法
{
	int next[MaxSize],i=0,j=0;
	GetNext(t,next);
	while (i=t.length)
		return(i-t.length);  	//返回匹配模式串的首字符下标
    else  
		return(-1);        		//返回不匹配标志
}

 看到这里，如果你已经全部理解了，请给自己鼓个掌，你已经成功攻破字符串两大难点算法之一的KMP算法！但是理解了还要多多体会算法思路，会懂得灵活运用才行！