笔记 CVPR 2021 Improving the Transferability of Adversarial Samples with Adversarial Transformations

摘要

 当前已有基于迁移的攻击由于对使用的局部模型过拟合，往往导致较低成功率。 因而作者提出通过对抗变换(adversarial transformations)来提升合成对抗样本的迁移性。 具体而言，作者使用一个对抗变换网络(adversarial transformation network )能够生成最有害的噪音，这种噪音能够破坏对抗扰动，同时要求生成的对抗样本能够抵抗这种对抗变换。

1 引入 Introduction

 基于迁移的攻击(transfer-based attacks)是指攻击者在本地模型上生成对抗样本，然后用此对抗样本来欺骗远程黑盒的模型。
 背景/已有工作:已有基于迁移的攻击往往对本地模型过拟合，从而迁移性低。先前工作主要致力于通过各种图像变换来提高迁移型，如调整大小(resizing), 变换(translation), 缩放(scaling)等。
 缺点:然而，上述工作只是使用单个图像变换，或者在固定的数量级下进行简单的组合。这样生成的对抗样本对于使用的图像变换过拟合，很难对抵抗未知的扰动，不能得到较好的迁移型。

 解决方案：解决上述问题，一个简单的方案就是找到一个丰富的图像变换集合，然后对每张图片进行精细的调节。但是这样会产生大量的计算量。于是，**作者提出利用一个对抗变换网络来自动控制这个扰动调节过程。图1为作者方法生成对抗样本的一个示例：

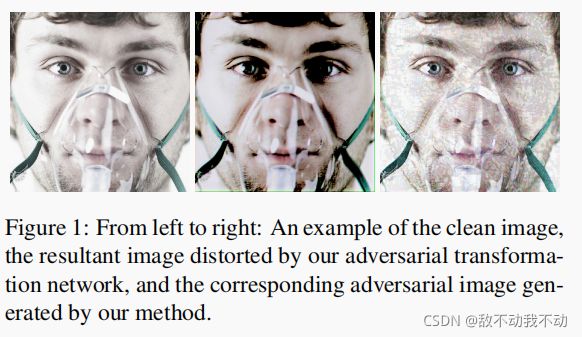
 图2为作者的Adversarial Transformation-enhanced Transfer Attack (ATTA)。作者受启发于CNN能够实现各种图像操纵任务，如数字水印、风格迁移，于是作者通过对抗训练训练一个CNN作为对抗变换网络，使得该网络能捕捉对对抗扰动最有害的变形。之后如果生成的对抗样本能够抵御对抗变换网络的变形/扰动，那此时的对抗样本鲁棒性、迁移性更好。

2 相关工作

2.1 合成对抗样本

 黑盒攻击可以分为两种：基于查询的(query-based)和基于迁移的攻击(transfer-based)。基于查询的攻击可能需要较高的查询代价，使攻击更容易被检测。与之对比，基于迁移的攻击使用本地模型作为替代来攻击，将生成的对抗样本用于攻击远程的目标模型。
 基于迁移的攻击往往由于对本地模型的过拟合，而表现出低成功率。为调高迁移型，已有的迁移攻击工作将对抗样本的生成看作一个优化问题，它们致力于改变传统的方案，来提高迁移性。在这个方向上，又可以分为两种:

1. 第一种使用更高级的优化算法，如动量，Nesterov加速梯度等。
2. 第二种受启发于数据增强策略。
    然而，第二种方法只考虑单独图像变换和在固定扰动扰动强度下的简单结合，这使得生成的对抗样本对使用的图像变换过拟合。

2.2 对抗样本防御

 防御对抗样本可以分为两个方法：一种是对抗训练，将对抗样本加入到训练集中；另一种是净化对抗样本，通常对输入图片进行预处理。

3 方法

3.1 问题描述

 定义：x表示一张干净图像，y为真实标签。f(x)为图像分类器，返回概率向量。于是对抗攻击的任务表示为：
$$argmaxf(x^{adv})\ne y,\text{\hspace{1em}(1)}$$
 
$$\parallel x^{adv}-x{\parallel }_p\le ϵ\text{\hspace{1em}(2)}$$

 (1)式是对抗样本攻击的目标，使目标模型分类错误。式(2)要求对抗样本扰动要小，人眼不可见。作者使用$L_{\infty }norm$来定义扰动的可见性。
 J(f(x),y)表示分类器f的损失函数，于是我们可以将对抗样本生成任务归结以下优化问题：
$$\begin{gathered} ma{x}_{x^{adv}}J(f(x^{adv}),y), \\ s.t.\parallel x^{adv}-x{\parallel }_{\infty }\ne ϵ\text{\hspace{1em}(3)} \end{gathered}$$
 式(3)是使用损失函数J(f(x),y)对式(1)的一个替代。

3.2 对抗变换网络 Adversarial Transformation Network

 用H表示图像变换函数，其参数为${\theta }_H$，H可能是多种简单图像变换的组合。H(x)表示对x进行后的图像。于是，我们将寻找对对抗样本最有害的图像变换归结为：
$$\begin{gathered} mi{n}_{{\theta }_H}ma{x}_{x^{adv}}J(f(H(x^{adv})),y), \\ s.t.\parallel x^{adv}-x{\parallel }_{\infty }\ne ϵ, \\ argmaxf(H(x))=y\text{\hspace{1em}(4)} \end{gathered}$$
 上式中，里面的最大化问题目的是寻找对抗样本$x^{adv}$，外侧的最小化问题是为了优化H的参数，来修正对抗样本，使其不再有害。
 对于式(4)的优化问题，如果先发现所有的候选图像变换，然后对每张对抗样本调节它们的组合以及强度，这个过程需要大量的计算。于是作者提出训练一个基于CNN的对抗变换网络来自动化调节对对抗样本最有害的变换。
 于是，变换函数H变为了一个卷积神经网络$T(x;{\theta }_T)$,其参数为${\theta }_T$。因而，式(4)变化为：
$$\begin{gathered} mi{n}_{{\theta }_T}ma{x}_{x^{adv}}J(f(T(x^{adv})),y), \\ s.t.\parallel x^{adv}-x{\parallel }_{\infty }\ne ϵ, \\ argmaxf(T(x))=y\text{\hspace{1em}(5)} \end{gathered}$$
 使用CNN来完成图像变换有两个好处：

1. CNN具有丰富的图像扰动能力。尽管图像变换函数H变为了CNN，图像变换空间依然很大。
2. CNN函数是一个端到端函数，它能自动调节图像变换。
    作者将对抗变换网络的损失函数定义为：
   $$L_T=J(f(T(x^{adv}),y)+{\alpha }_{1}J(f(T(x)),y)+{\alpha }_2\parallel x^{adv}-T(x^{adv}){\parallel }^2\text{\hspace{1em}(6)}$$
    式(6)中第一项表示对抗变换网络反对抗扰动的追求， 第二项要求对抗变换网络保持原始图像的内容，最后一项限制了对抗变换网络的变换强度，它的作用是一个正则化，避免过拟合。作者使用$l_{2}norm$。
    式(5)中，对于内层的最大化问题，作者使用目标函数$L_{fool}$如下。第二项使用目标模型的损失函数的替代来寻找对抗样本。第一项中加入了对抗变换网络的变形，目的是使生成的对抗样本能够抵御对抗变换网络的变换。
   $$L_{fool}=-J(f(T(x^{adv})),y)-\beta J(f(x^{adv}),y)\text{\hspace{1em}(7)}$$
    基于以上损失函数函数定义，对抗变换网络的训练过程如下图。简单来说，就是交替进行搜寻对抗样本和对抗变换网络训练两个过程。
   

3.3 对抗样本生成

 对抗变换网络训练完成后，作者将其作为一个预处理模块，放在目标分类模型前面，如图2所示。

 此时，将对抗变换网络和图像分类器作为另一个受害者模型来攻击。目标攻击函数为:
$$L_{attack}=J(f(x^{adv},y)+\gamma J((T(x^{adv})),y)\text{\hspace{1em}(8)}$$
 基于式(8)，可以使用任何优化算法来寻找解。作者使用来基础的迭代方法，具体如算法2所示:

4 实验

4.1 实验设置

 作者聚焦于攻击使用ImageNet数据集训练的图像分类器。
数据集： 作者使用ILSVRC 2012训练部分，作为develop set,来实施攻击，训练对抗变换网络。测试数据使用的ILSVRC 2012de1验证集。
目标模型:目标模型包含来了非防御模型和防御模型。非防御模型有ResNet v2(Res-v2), Inception v3(Inc-v3), Inception v(Inc-v4), 和Inception-ResNet v2(IncRes-v2)。防御模型有对抗训练的Inception-ResNet v2($IncRes-v{2}_{adv}$， 和对抗训练的Incepiton v3(分别整合三个模型、四个模型的对抗样本)($Inc-v{3}_{ens3}$和$Inc-v{3}_{ens4}$)

参数：作者的对抗变换模型采用了两层的CNN: 33卷积层、 Leaky ReLU和163卷积层。
 $ϵ=16,K、K_{outer}和K_{inner}均为10，{\alpha }_1，{\alpha }_2，\beta 和\gamma 分别为1.0,10,1.0和1.0。$

4.2 攻击结果

 表2展现了使用Inc-v3作为源模型，来攻击其他有防御机制的模型。

4.3 进一步分析

 作者对对抗变换网络的结构做了消融实验，如下图。图中Conv(a,b,…)表明每层卷积网络的核大小。
 表3表明，过于简单和复杂的结构都会退化攻击效果，原因在于前者没有足够的表征能力，而后者会使对抗样本对攻击算法过拟合。

4.4 作者研究的互补( Complementary Effect of Our Technique)

 作者的研究可以与其他基于迁移的攻击进行结合。作者将研究与SI-NI-TI-DIM结合，试验结果见表4.

5 总结