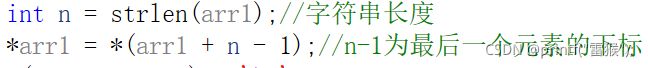细!小白函数递归大总结!码住!
目录
#前言
#一、什么是递归
#二、递归的必要条件
#三、递归的步骤
#四、递归的一些应用例题
熬夜早起肝博客!!冲!!
#前言
大家好,今天给大家带来递归初步学习的大总结,对刚接触递归的同学来讲是一个非常不错的巩固与练习,希望大家有所收获。
#一、什么是递归
程序调用自身的编程技巧称为递归( recursion)。
递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接
调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的核心思想(主要思考方式)是把大事化为小事
#二、递归的必要条件
1.存在限制条件,当满足这个限制条件的时候,递归便不再继续。
2.每次递归调用之后越来越接近这个限制条件。
#三、递归的步骤
1.函数递归时,每次调用一次函数,计算机都会在内存栈区为函数开辟一个新的空间,也就是说
如果递归层次过深,会导致栈区空间不足,也就是所谓的栈溢出(Stack Overflow),使用VS2019编译器时若递归层次过深则会发生报错,在下面解释斐波那契数列时也会在做说明
2.函数递归结束函数开始返回,开辟的空间开始释放
切记!函数递归调用函数时从外层一层一层进入内层,返回函数时从内层一层一层返回出外层!
#四、递归的一些应用例题
下面的例题会贯彻上面的递归思想(即把大事化小)
1.逐个打印一个多位数的各个位
先上代码
#include
void print(int num)
{
if (num > 9)
{
print(num / 10);
}
printf("%d ", num%10);
}
int main()
{
int ret = 0;
scanf("%d",&ret);//1234,
print(ret);
return 0;
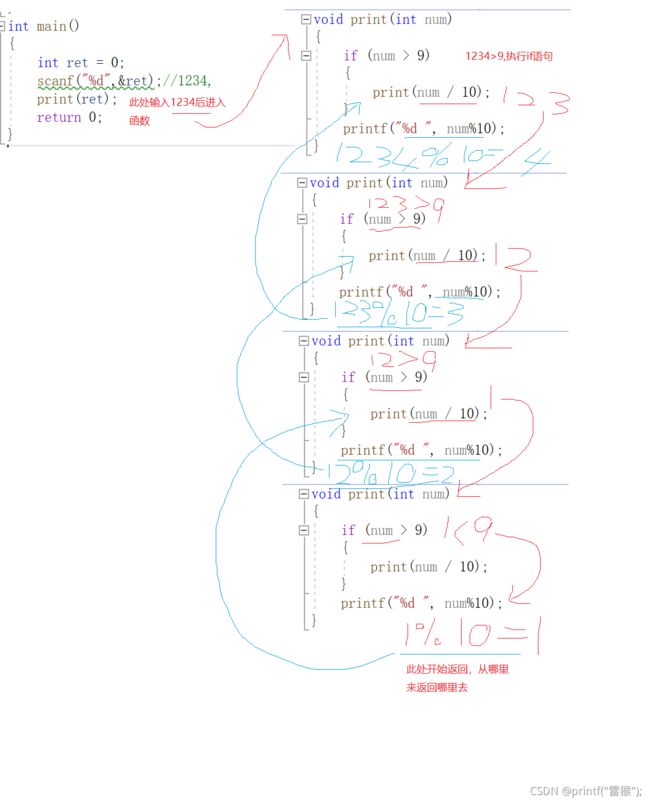
} 下面通过画图的方式对该题进行讲解,我们假定输入的值为1234
注意打印的顺序,程序是按箭头的顺序开始执行!红色箭头执行完后开始执行蓝色箭头(返回时深一层函数完全执行完后再返回到浅一层函数,浅一层函数再开始执行下面语句),因此按顺序打印后结果应该是1 2 3 4,程序运行结果:
这道题一定要好好体会函数递归语句执行的顺序,特别是函数返回的时候
第一题的函数采用void定义,没有向主函数返回值,下面来一个有向主函数返回值的
2.计算n的阶乘
还是先上代码!
#include
int jc(int n)
{
int ret = 0;
if (n < 2)
{
return 1;
}
else
{
return n * jc(n - 1);
}
}
int main()
{
int n = 0;
printf("请输入一个值n\n");
scanf("%d", &n);
printf("%d的阶乘=%d ",n,jc(n));
return 0;
} 这里函数里面定义的ret没用,手误
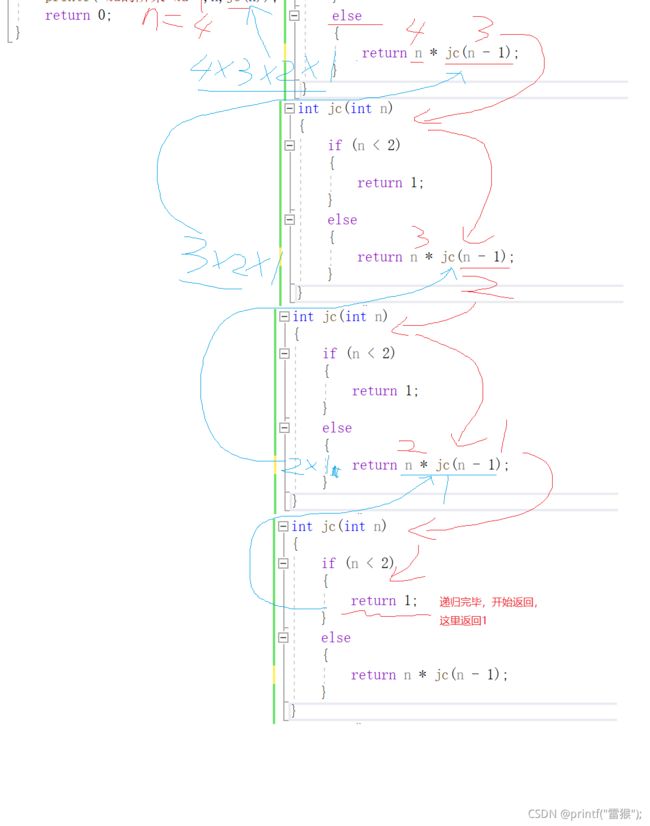
还是采用画图的方式对本题进行详细讲解
这里我们假设n=4
这一道题可以更加深化理解函数递归返回时的步骤,从内到外开始返回,下面贴上程序执行结果:
3.递归模拟strlen测量数组长度
代码:
#include
int _strlen(char *arr)
{
if (*arr == '\0')
{
return 0;
}
else
{
return 1 + _strlen(arr + 1);
}
}
int main()
{
char arr[20]= {"abcdefg"};
printf("长度=%d ", _strlen(arr));
return 0;
} 注意!调用函数时函数参数arr代表的是arr[20]中首元素的地址,因此定义函数时接收参数的形参为指针变量,该题与上一题思路相同,不做赘述。只讲一点,*是解义字符,arr是地址,那*arr即代表解地址,那就是字符串中的元素,又字符串的结束标志是\0,故函数部分如上图呈现
下面是程序执行结果:
![]()
(此处也说明了字符串结束标志并不算在长度里面)
怎么样是不是忽然感觉用递归很牛逼很牛逼哈哈哈哈哈哈,有没有犯迷糊的地方呢
4.斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)——源自百度百科
简单理解为数列下一项等于前两项之和
先上代码
#include
int Fibon(int n)
{
if (n <= 2)
return 1;
else
return Fibon(n - 1) + Fibon(n - 2);
}
int main()
{
int n = 0;
int ret = 0;
scanf("%d", &n);
ret = Fibon(n);
printf("ret=%d", ret);
return 0;
}
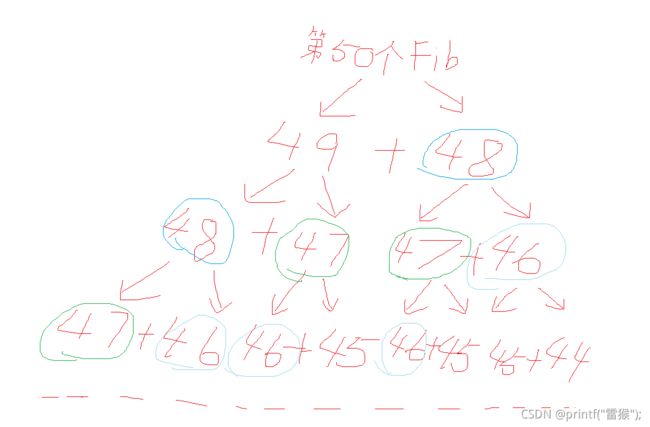
有了上面的公式,这一段递归很好理解,但这道题的重点不在这里,大家可以试运行一下n=50,在一分钟之内电脑应该是不能给出结果的,在n<=35时计算机可以秒给出答案,那么这是为什么呢?我们来看下面的图,假设n为50(此处Fib代指斐波那契)
可以发现只进行了几次调用,计算机已经做了大量重复运算,那当n足够大时,这个重复运算的量可谓相当庞大,因此大大减慢了代码的运算速度,甚至导致栈溢出
因此这个题用迭代实现更好(用递归能实现的都可以用迭代实现) ,代码如下
#define _CRT_SECURE_NO_WARNINGS 1
#include
int Fibon(int n)
{
int a = 1;
int b = 1;
int c = 0;
int i = 0;
if (n <= 2)
{
return 1;
}
else
{
for (i = 0; i < (n - 2); i++)
{
c = a + b;
a = b;
b = c;
}
return c;
}
}
int main()
{
int n = 0;
int ret = 0;
scanf("%d", &n);
ret = Fibon(n);
printf("ret=%d", ret);
return 0;
} 只需注意一点,for循环中计算完前两项的和(a+b)后,要将a赋值为b,b赋值为a+b的和,即将a,b均向后移一项,这样才可以计算下下一项的和。
有公式是不是递归变的异常简单,反而迭代写法还需要一些思考呢,所以是否使用递归是需要根据情况选择的
5.递归实现字符串逆序
即如果输入的字符串是abcdef,则输出fedcba
本题也可用迭代写出且较递归更为简洁明了,可以尝试,这里不再给出代码,下面讲解迭代做法
代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include
void nixu(char* arr1)
{
char linshi = *arr1;
int n = strlen(arr1);//字符串长度
*arr1 = *(arr1 + n - 1);//n-1为最后一个元素的下标
*(arr1 + n - 1) = '\0';
if (strlen(arr1 + 1) >= 2)
{
nixu(arr1 + 1);
}
*(arr1 + n - 1) = linshi;
}
int main()
{
char arr[] = { "abcdef" };
nixu(arr);
printf("%s", arr);
return 0;
} 下面画图来细细理清这段代码
逆序无非是让字符串中的元素一对一对的对调,注意接下来的思路!
递归,把大事化小事
我们把abcdef的逆序拆为af的逆序加bcde的逆序,把bcde的逆序再拆为ce的逆序加cd的逆序,那递归的思路不就出来了吗,我们需要做的就是把第一层函数调用写清楚,接下来只不过是计算机的重复运算罢了。接下来单独分析函数部分
稍作解释:*arr1表示字符串中第一个元素*arr+n(字符串长度)-1为字符串最后一个元素
接下来做四步!:
第一步:把首元素的值赋给一个临时储存用的变量
![]()
这一步是为了存储第一个元素,以便把最后一个元素放到第一个元素的位置
第二步:把最后一次元素放到第一个元素的位置
注意这里需要先求字符串长度,因为字符串最后一个元素下标为长度-1 (为了方便直接用了strlen函数,其实也可以用上面写的代码替换)
第三步:把字符串最后一个元素换为/0
这一步非常重要,因为字符串的结束标志是\0,只有这样进行递归时才能继续进行,换完后现在如下图
这里a还被存储在外面
第五步:把新的字符串进行逆序,即"bcde\0"
arr1+1表示数组第二个元素,所以新的字符串为 "bcde\0",需要注意的是这个判断条件,当新的字符串长度大于等于2时,才继续进行调用,若长度为0或1,如原始字符串为"ab"(为0)、"abc"(为1)这些都是进行一次交换后已经完成逆序的,因此不需要再进行下面的逆序,逆序已经完成
第六步:当所有元素完成逆序后,把a放到最后一个元素
至此所有步骤完成
下面来重新理顺:
1.将首元素单独拿出,放到一个临时变量存储
2.将末元素放到首元素的位置
3.在末元素的位置上放\0以便进行下一次字符串逆序
4.新的字符串(即去除原本字符串首元素和末元素的字符串)进行逆序
5.在所有元素完成逆序后把首元素放到末元素的位置
注意其中第四步我们不需要去考虑是怎么实现的,这一步其实就是递归思想的核心,把大事化小,我们只需要去做最小的那一件事,剩下的不需要我们管。
代码运行结果:
6.递归经典问题之汉诺塔问题 汉诺塔
7.递归查找自定义数组最大值 数组
以上两个问题在前两次博客中已经做了详细解释,大家有需要可以点击链接查看
最后来看一个非常有意思的题目,
青蛙跳台阶问题
首先来看普通青蛙跳台阶!
问题描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)
先进行列举
n=1时,1种,直接跳上去
n=2时,2种,直接跳上去或者一个一个跳
n=3时,3种,(1,1,1)(2,1)(1,2)
n=4时, 5种,(1,1,1,1)(1,1,2)(1,2,1)(2,1,1)(2,2)
n=5时, 8种,(1,1,1,1,1)(1,1,1,2)(1,1,2,1)(1,2,1,1)(2,1,1,1)(1,2,2)(2,1,2)(2,2,1)
是不是似曾相识啊,这不是刚刚讲过的斐波那契数列吗!如果我们再假定一个n=0时,青蛙只能不跳,那不也是一种吗。
那这里怎么理解呢,青蛙跳3层台阶时,分为1层台阶+2层台阶,也就是说青蛙跳台阶的方法是跳1层台阶的方法+跳2层台阶的方法
跳4层台阶时,若青蛙某一次跳上1层台阶,则剩下3层台阶,若跳上2层台阶,则剩下2层台阶,所以跳4层台阶时的方法是跳3层台阶的方法+跳2层台阶的方法
跳5层台阶时,还是跳1或者跳2的问题,跳1那么接下来的4层就按4层台阶的方法来跳,跳2那么接下来的3层就按3层台阶的方法来跳,所以跳5层台阶的方法是跳4层台阶的方法+跳3层台阶的方法
以此类推
跳n层台阶的方法数量(n>2)F(n)=F(n-1)+F(n-2),还真和斐波那契数列表达式一样,因此代码省略,接下来我们来看看重量级的超人青蛙选手(有点难)
与普通青蛙不一样的是,超人青蛙可以一次跳多个台阶,多多少呢?无数个,对就是这么离谱
先假设青蛙现在可以跳3节台阶了
n=1时,1种,直接跳上去
n=2时,2种,直接跳上去或者一个一个跳
n=3时,4种,(1,1,1)(2,1)(1,2)(3)
n=4时,7种,(1,1,1,1)(1,1,2)(1,2,1)(2,1,1)(2,2)(1,3)(3,1)
n=5时,13种,(1,1,1,1,1)(1,1,1,2)(1,1,2,1)(1,2,1,1)(2,1,1,1)(1,2,2)(2,1,2)(2,2,1)(1,1,3)(1,3,1)(3,1,1)(2,3)(3,2)
总结出规律:F(n)=F(n-1)+F(n-2)+F(n-3)
那么我们大胆推测,当可以跳N层台阶时
F(n)=F(n-1)+F(n-2)+F(n-3)+……+F(n-N+1)+F(n-N)共加了N项(n>N)
代码:
这里代码我还没想出来,对于现在的我还是过于复杂了,在未来的某一天我会重新回来补充的,哈哈哈哈哈哈哈哈哈
到此为止初识递归就结束了,如果把这篇博客的每一个例题都吃透的话我相信一定会收获颇丰,从刚接触递归的小白到能使用递归可能只差几遍代码,关于递归我一共写了三篇博客,在一段时间内可能不会再更新关于递归的内容,希望在未来的学习中不断深化对递归的理解、应用,有朝一日能写出自己对递归的更深理解!
如果觉得文章有用请给个小手加评论鼓励哦!!!谢谢!!