力扣刷题系列——回溯算法I
回溯算法思想及经典例题(一)
回溯法
可以提前看看公众号文章:https://mp.weixin.qq.com/s/g5uvxi1lyxmWC4LtP0Bdlw (从二叉树遍历到回溯算法,包含例题:二叉树路径和等于给定目标值的路径(力扣113)、集合的所有子集合列表(力扣78))
1、概念
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
2、基本思想
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。
若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。
而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
回溯法中,首先需要明确下面三个概念:
(一)约束函数:约束函数是根据题意定出的。通过描述合法解的一般特征用于去除不合法的解,从而避免继续搜索出这个不合法解的剩余部分。因此,约束函数是对于任何状态空间树上的节点都有效、等价的。
(二)状态空间树:刚刚已经提到,状态空间树是一个对所有解的图形描述。树上的每个子节点的解都只有一个部分与父节点不同。
(三)扩展节点、活结点、死结点:所谓扩展节点,就是当前正在求出它的子节点的节点,在深度优先搜索中,只允许有一个扩展节点。活结点就是通过与约束函数的对照,节点本身和其父节点均满足约束函数要求的节点;死结点反之。由此很容易知道死结点是不必求出其子节点的(没有意义)。
3、用回溯法解题的一般步骤:
首先,要通过读题完成下面三个步骤:
(1)描述解的形式,定义一个解空间,它包含问题的所有解。
(2)构造状态空间树。
(3)构造约束函数(用于杀死节点)。
然后就要通过深度优先搜索思想完成回溯,完整过程如下:
(1)设置初始化的方案(给变量赋初值,读入已知数据等)。
(2)变换方式去试探,若全部试完则转(7)。
(3)判断此法是否成功(通过约束函数),不成功则转(2)。
(4)试探成功则前进一步再试探。
(5)正确方案还未找到则转(2)。
(6)已找到一种方案则记录并打印。
(7)退回一步(回溯),若未退到头则转(2)。
(8)已退到头则结束或打印无解。
4、算法框架
(1)问题框架
设问题的解是一个n维向量(a1,a2,………,an),约束条件是ai(i=1,2,3,…..,n)之间满足某种条件,记为f(ai)。
(2)非递归回溯框架
int a[n],i;
初始化数组a[];
i = 1;
while (i>0(有路可走) and (未达到目标)) // 还未回溯到头
{
if(i > n) // 搜索到叶结点
{
搜索到一个解,输出;
}
else // 处理第i个元素
{
a[i]第一个可能的值;
while(a[i]在不满足约束条件且在搜索空间内)
{
a[i]下一个可能的值;
}
if(a[i]在搜索空间内)
{
标识占用的资源;
i = i+1; // 扩展下一个结点
}
else
{
清理所占的状态空间; // 回溯
i = i –1;
}
}(3)递归的算法框架
回溯法是对解空间的深度优先搜索,在一般情况下使用递归函数来实现回溯法比较简单,其中i为搜索的深度,框架如下:
int a[n];
try(int i)
{
if(i>n)
输出结果;
else
{
for(j = 下界; j <= 上界; j=j+1) // 枚举i所有可能的路径
{
if(fun(j)) // 满足限界函数和约束条件
{
a[i] = j;
... // 其他操作
try(i+1);
回溯前的清理工作(如a[i]置空值等);
}
}
}
}回溯法有“通用解题法”之称。用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
例题讲解
(力扣46)给定一个不重复的数字集合,返回其所有可能的全排列。例如:
-
输入:
[1, 2, 3] -
输出:
[ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
代码实现:
class Solution {
public List> permute(int[] nums) {
List> lists = new ArrayList<>();
int[] arr = new int[nums.length];
backTrack(lists,nums,new ArrayList(),arr);
return lists;
}
public void backTrack(List> lists,int[] nums,ArrayList list,int[] arr){
if(list.size()==nums.length){
lists.add(new ArrayList(list));
return;
}
for(int i=0;i 下面以经典的排列(permutation)和组合(combination)问题为例,讲讲求解回溯法问题的要点:候选集合。
内容将会包含:
-
回溯法的”选什么“问题与候选集合
-
全排列、排列、组合问题的回溯法解法
-
回溯法问题中,如何维护候选集合
-
回溯法问题中,如何处理失效元素
回溯法的重点:“选什么”
我们说过,回溯法实际上就是在一棵决策树上做遍历的过程。那么,求解回溯法题目时,我们首先要思考所有决策路径的形状。例如,子集问题的决策树如下图所示:
![]()
子集问题的决策树
决策树形状主要取决于每个结点处可能的分支,换句话说,就是在每次做决策时,我们 “可以选什么”、 “有什么可选的”。
对于子集问题而言,这个“选什么”的问题非常简单,每次只有一个元素可选,要么选、要么不选。不过,对于更多的回溯法题目,“选什么”的问题并不好回答。这时候,我们就需要分析问题的候选集合,以及候选集合的变化,以此得到解题的思路。
全排列问题:如何维护候选集合
让我们拿经典的全排列问题来讲解回溯法问题的候选集合概念。
在全排列问题中,决策树的分支数量并不固定。我们一共做 n 次决策,第 i 次决策会选择排列的第 i 个数。选择第一个数时,全部的 n 个数都可供挑选。而由于已选的数不可以重复选择,越往后可供选择的数越少。以 n=3 为例,决策树的形状如下图所示:
![]()
全排列问题的决策树
如果从候选集合的角度来思考,在进行第一次选择时,全部的 3 个数都可以选择,候选集合的大小为 3。在第二次选择时,候选集合的大小就只有 2 了;第三次选择时,候选集合只剩一个元素。可以看到,全排列问题候选集合的变化规律是:每做一次选择,候选集合就少一个元素,直到候选集合选完为止。我们可以在上面的决策树的每个结点旁画上候选集合的元素,这样看得更清晰。
![]()
全排列问题有候选集合的决策树
可以看到,已选集合与候选集合是补集的关系,它们加起来就是全部的元素。而在回溯法的选择与撤销选择的过程中,已选集合和候选集合是此消彼长的关系。
如何根据这样的思路写出代码呢?当然可以用 HashSet 这样的数据结构来表示候选集合。但如果你这么去写的话,会发现代码写起来比较啰嗦,而且 set 结构的“遍历-删除”操作不太好写。在这里,我不展示使用 set 结构的代码。大家只要明白一条要点:在一般情况下,候选集合使用数组表示即可。 候选集合上需要做的操作并不是很多,使用数组简单又高效。
在子集问题中,我们定义了变量 k,表示当前要对第 k 个元素做决策。实际上,变量 k 就是候选集合的边界,指针 k 之后的元素都是候选元素,而 k 之前都是无效元素,不可以再选了。
![]()
用数组表示候选集合
而每次决策完之后将 k 加一,就是将第 k 个元素移出了候选集合。
![]()
将第 k 个元素移出候选集合
在全排列问题中,我们要处理的情况更难一些。每次做决策时,候选集合中的所有元素都可以选择,也就是有可能删除候选集合中间的元素,这样数组中会出现“空洞”。这种情况该怎么处理呢?我们可以使用一个巧妙的方法,先将要删除的元素与第 k 个元素交换,再将 k 加一,过程如下方动图所示:
![]()
不知道你有没有注意到,上图中候选集合之外的元素画成了蓝色,这些实际上就是已选集合。前面分析过,已选集合与候选集合是互补的。将蓝色部分看成已选集合的话,我们从候选集合中删除的元素,正好加入了已选集合中。也就是说,我们可以只用一个数组同时表示已选集合和候选集合!
理解了图中的关系之后,题解代码就呼之欲出了。我们只需使用一个 current 数组,左半边表示已选元素,右半边表示候选元素。指针 k 不仅是候选元素的开始位置,还是已选元素的结束位置。我们可以得到一份非常简洁的题解代码:
public List> permute(List nums) {
List current = new ArrayList<>(nums);
List> res = new ArrayList<>();
backtrack(current, 0, res);
return res;
}
// current[0..k) 是已选集合, current[k..N) 是候选集合
void backtrack(List current, int k, List> res) {
if (k == current.size()) {
res.add(new ArrayList<>(current));
return;
}
// 从候选集合中选择
for (int i = k; i < current.size(); i++) {
// 选择数字 current[i]
Collections.swap(current, k, i);
// 将 k 加一
backtrack(current, k+1, res);
// 撤销选择
Collections.swap(current, k, i);
}
} 注意写在递归函数上方的注释。在写回溯法问题的代码时,你需要时刻清楚什么是已选集合,什么是候选集合。注释中的条件叫做“不变式”。一方面,我们在函数中可以参考变量 k 的含义,另一方面,我们在做递归调用的时候,要保证这个条件始终成立。特别注意代码中递归调用传入的参数是 k+1 ,即删除一个候选元素,而不是传入 i+1。
n 中取 k 的排列
![]()
n 中取 k 的排列的决策树
题解代码如下所示,只需要修改递归结束的条件即可。
public List> permute(List nums, int k) {
List current = new ArrayList<>(nums);
List> res = new ArrayList<>();
backtrack(k, current, 0, res);
return res;
}
// current[0..m) 是已选集合, current[m..N) 是候选集合
void backtrack(int k, List current, int m, List> res) {
// 当已选集合达到 k 个元素时,收集结果并停止选择
if (m == k) {
res.add(new ArrayList<>(current.subList(0, k)));
return;
}
// 从候选集合中选择
for (int i = m; i < current.size(); i++) {
// 选择数字 current[i]
Collections.swap(current, m, i);
backtrack(k, current, m+1, res);
// 撤销选择
Collections.swap(current, m, i);
}
} 注意这里 k 是题目的输入,所以原先我们代码里的变量 k 重命名成了 m。此外,就是递归函数开头的 if 语句条件发生了变化,当已选集合达到 k 个元素时,就收集结果停止递归。
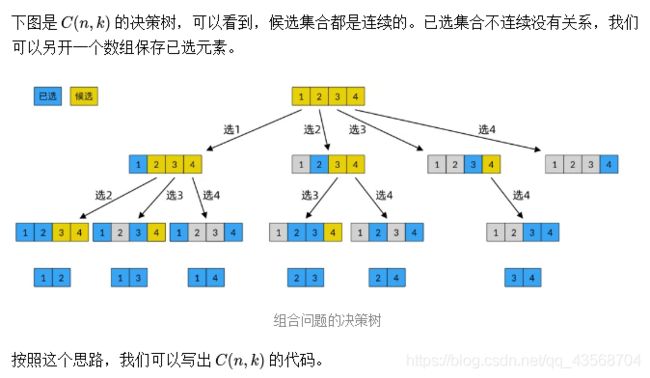
组合问题:失效元素
![]()
public List> combine(List nums, int k) {
Deque current = new ArrayDeque<>();
List> res = new ArrayList<>();
backtrack(k, nums, 0, current, res);
return res;
}
// current 是已选集合, nums[m..N) 是候选集合
void backtrack(int k, List nums, int m, Deque current, List> res) {
// 当已选集合达到 k 个元素时,收集结果并停止选择
if (current.size() == k) {
res.add(new ArrayList<>(current));
return;
}
// 从候选集合中选择
for (int i = m; i < nums.size(); i++) {
// 选择数字 nums[i]
current.addLast(nums.get(i));
// 元素 nums[m..i) 均失效
backtrack(k, nums, i+1, current, res);
// 撤销选择
current.removeLast();
}
} 由于已选集合与候选集合并非互补,这里用单独的数组存储已选元素,这一点上与子集问题类似。
组合问题与子集问题的关系
也许是排列 & 组合的 CP 感太重,所以我们在思考组合问题的解法的时候会自然地从排列问题上迁移。其实,组合问题和子集问题有很密切的联系。
由子集问题求解组合问题
组合问题可以看成是子集问题的特殊情况。从 n 中取 k 个数的组合,实际上就是求 n 个元素的所有大小为 k 的子集。也就是说,组合问题的结果是子集问题的一部分。我们可以在子集问题的决策树的基础上,当已选集合大小为 k 的时候就不再递归,就可以得到组合问题的决策树。
![]()
在子集问题决策树基础上得到的组合问题决策树
public List> subsets(List nums) {
Deque current = new ArrayDeque<>();
List> res = new ArrayList<>();
backtrack(nums, 0, current, res);
return res;
}
// current 是已选集合, nums[m..N) 是候选集合
void backtrack(List nums, int m, Deque current, List> res) {
// 收集决策树上每一个结点的结果
res.add(new ArrayList<>(current));
if (m == nums.size()) {
// 当候选集合为空时,停止递归
return;
}
// 从候选集合中选择
for (int i = m; i < nums.size(); i++) {
// 选择数字 nums[i]
current.addLast(nums.get(i));
// 元素 nums[m..i) 均失效
backtrack(nums, i+1, current, res);
// 撤销选择
current.removeLast();
}
} 可以看到,每次做决策都会增加一个已选元素。当递归到第 k 层时,计算的就是大小为 k 的子集。不过,这样写出的子集问题解法没有原解法易懂,我还是更推荐原解法。
经典例题
1.分割回文串
(力扣131)给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: "aab"
输出:
[
["aa","b"],
["a","a","b"]
]
代码实现:
//https://leetcode-cn.com/problems/palindrome-partitioning/solution/hui-su-you-hua-jia-liao-dong-tai-gui-hua-by-liweiw/
class Solution {
public List> partition(String s) {
List> lists = new ArrayList<>();
if(s==null) return lists;
int len = s.length();
LinkedList list = new LinkedList<>();
backtracking(s,0,len,list,lists);
return lists;
}
public void backtracking(String s,int start,int end,LinkedList list,List> lists){
if(start == end){
lists.add(new ArrayList(list));
return;
}
for(int i=start;i 2.组合总和
(力扣216)找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
代码实现:
class Solution {
List> ans = new ArrayList<>();
//尽量不要使用遗留类Stack,Deque完成可以实现Stack功能。
Deque path = new ArrayDeque<>();
/**
* 整体思路
*
* @param k k个数
* @param n 组合成n(累加和为n)
* 组合数范围1~9,且不重复
* @return
*/
public List> combinationSum3(int k, int n) {
dfs(k, n, 1);
return ans;
}
/**
* @param k k个数
* @param n 组合成n(累加和为n)
* @param start 组合数范围start~9,且不重复
*/
private void dfs(int k, int n, int start) {
if (k < 0 || n < 0) return; // 剪枝
// 刚好k个数、刚好递减成0(说明这k个数累加和刚好为n)
if (k == 0 && n == 0) {
if (!path.isEmpty())
ans.add(new ArrayList<>(path));
return;
}
// 从start开始,到9的范围,然后就是递归分支(选、不选) 记得恢复状态
for (int i = start; i < 10; i++) {
path.push(i);
dfs(k - 1, n - i, ++start);
path.pop();
}
}
} 3.递增子序列
(力扣491)给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
输入: [4, 6, 7, 7]
输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
- 给定数组的长度不会超过15。
- 数组中的整数范围是 [-100,100]。
- 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
代码实现:
class Solution {
List temp = new ArrayList();
List> ans = new ArrayList>();
public List> findSubsequences(int[] nums) {
dfs(0, Integer.MIN_VALUE, nums);
return ans;
}
public void dfs(int cur, int last, int[] nums) {
if (cur == nums.length) {
if (temp.size() >= 2) {
ans.add(new ArrayList(temp));
}
return;
}
if (nums[cur] >= last) {
temp.add(nums[cur]);
dfs(cur + 1, nums[cur], nums);
temp.remove(temp.size() - 1);
}
if (nums[cur] != last) {
dfs(cur + 1, last, nums);
}
}
} 4.幂集
(力扣1698,面试题08.04)幂集。编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
代码实现:
class Solution {
public List> subsets(int[] nums) {
//结果集合
List> list = new ArrayList();
//回溯方法
backtrack(list,new ArrayList<>(),nums,0);
return list;
}
public void backtrack(List>list,ListtempList,int []nums,int start){
list.add(new ArrayList<>(tempList));
for(int i = start;i 5.有重复字符串的排列组合
(力扣1702,面试题08.08)有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。
示例1:
输入:S = "qqe"
输出:["eqq","qeq","qqe"]
示例2:
输入:S = "ab"
输出:["ab", "ba"]
提示:
- 字符都是英文字母。
- 字符串长度在[1, 9]之间。
代码实现:
import java.util.List;
import java.util.Arrays;
class Solution {
public String[] permutation(String S) {
List res = new ArrayList();
int len = S.length();
if (len == 0) return new String[0];
boolean[] used = new boolean[len];
char[] sChar = S.toCharArray();
StringBuilder path = new StringBuilder(len);
// 排序是为了后面的剪枝
Arrays.sort(sChar);
dfs(res, sChar, len, path, 0, used);
return res.toArray(new String[0]);
}
/**
* @param res 结果集
* @param sChar 输入字符数组
* @param len 字符数组长度
* @param path 根结点到任意结点的路径
* @param depth 当前树的深度
* @param used 使用标记数组
*/
private void dfs(List res
, char[] sChar
, int len
, StringBuilder path
, int depth
, boolean[] used) {
// 到达叶子结点
if (depth == len) {
res.add(path.toString());
return;
}
for (int i = 0; i < len; i++) {
if (!used[i]) {
// 根据已排序字符数组, 剪枝
if (i > 0 && sChar[i] == sChar[i-1] && !used[i-1]) {
continue;
}
path.append(sChar[i]);
used[i] = true; // 标记选择
dfs(res, sChar, len, path, depth+1, used);
path.deleteCharAt(depth);
used[i] = false; // 撤销选择
}
}
}
} 以上内容整合了几方资源,仅作为个人日后复习查阅,侵删。