想进进字节、阿里等一线大厂，刷算法前一定先打好底层基础

作者： Tom哥
简介：计算机研究生，校招进阿里，期间还拿过百度、华为、中兴、腾讯等6家大厂offer，P7 技术专家。出过专利，CSDN博客专家。
公众号：微观技术，分享其他地方看不到的知识与思考，欢迎关注

大家好，我是Tom哥~

哲学里有一句很经典的话，”下层基础决定上层建筑“。相信很多人都听过，广泛用于我们生活中。

那么我们软件开发行业的下层基础是什么，有人说是操作系统、是网络、是HTTP协议、是TCP，这些虽然也是底层，但其实不够原子化。

软件行业讲究的是抽象，那么他们的共同点是什么。那就是数据和计算。

1、数组

定义：

数组是一组连续内存空间存储的具有相同类型的数据，整个排列像一条线一样，是一种线性表数据结构。

划重点：

• 连续内存空间

• 相同数据类型

• 线性结构

像常见的数组、链表、栈、队列，都是线性结构。

优势：

随机访问。为什么呢？因为他的类型固定，决定它的数据长度也就固定，另外就是连续，所以基于初始地址，可以直接计算出数组任意位置的内存地址。查询速度很多。

缺点：

• 为了保持连续性，中间位置插入或删除数据，需要做数据搬移，效率会较低。可以看下ArrayList相关API的源码

• 成也萧何败萧何，数组初始化需要连续的内存空间，如果空间不够怎么办？我们可以选择 链表

注意点：

• 使用数组要注意越界问题

• 数组扩容需要申请内存、数据搬移，成本较大，如果开始时能确定大小，那么在初始化时指定其大小。

2、链表

定义：

链表一种非连续、非顺序的存储结构，由一系列节点组成，节点间通过指针完成了串联，每个节点包含数据和下一个节点指针两部分。

根据指针的方向可以分为：

• 单向链表

• 循环链表

• 双向链表

• 双向循环链表

划重点：

• 不需要连续内存空间

• 通过指针将这些空间串起来，形成一条链

优势：

• 不需要连续的内存空间，较灵活

• 允许插入、删除链表上任意位置的节点，只需要修改指针的值，不需要像数组一样搬移数据，系统开销成本大大降低

缺点：

• 链表除了存储数据，还要存储指针，会额外占用一些存储空间

• 由于非顺序存储，所以不支持随机存取

注意点：

数组擅长按下标随机访问，链表擅长插入、删除操作。平常大家使用时，根据具体使用场景是读多还是写多灵活选择。

3、栈

定义：

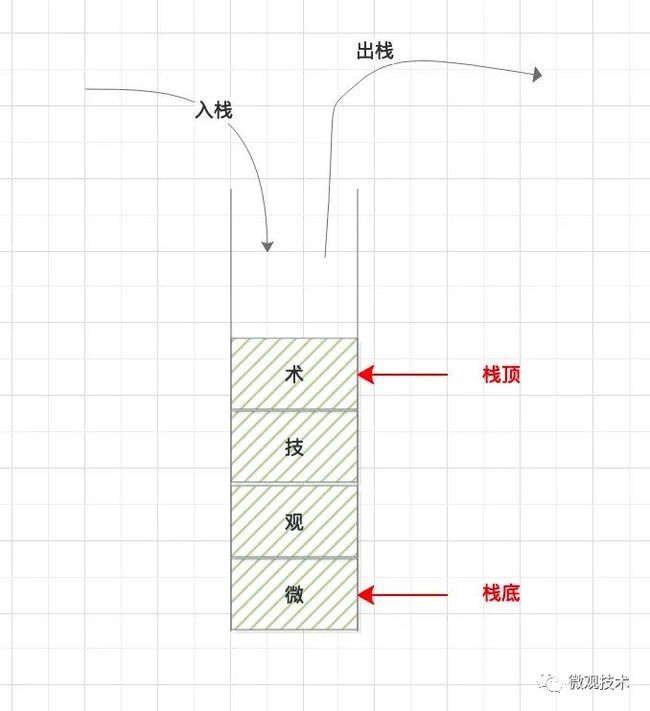
又名堆栈，它是一种运算受限的线性表。上面成为栈顶，下面称为栈底。向栈插入新元素称为入栈，新元素放到栈顶；从一个栈删除元素又称作出栈，它是把栈顶元素删除掉，使其下面相邻的元素成为新的栈顶元素。

根据底层结构不同，可以分为数组实现的顺序栈、链表实现的链式栈。

划重点：

• 两个动作：入栈、出栈

• 先进后出，后进先出

优势：

• 只能操作栈顶元素，规则限制的死死地，不像其他数据结构非常灵活，可控性好，非常适合一些特殊业务场景

缺点：

• 只能从上往下依次读取，不能从中间读取数据

典型场景：

• JVM的本地方法栈，函数调用

• 浏览器的前进、后退

4、队列

定义：

队列是一种特殊的线性表，只允许在表的前端进行删除操作，而在表的后端进行插入操作。和栈一样，队列是一种操作受限制的线性表。插入的数据放在队尾，读取数据的端称为队头。队列中没有元素时，称为空队列。

根据支持的高级特性，可以分为：循环队列、阻塞队列、并发队列。根据底层结构不同，可以分为顺序队列、链式队列。

划重点：

• 两个动作：入队、出队

• 需要两个指针，一个head指针，指向队头；一个tail指针，指向队尾。随着入队和出队，两个指针也会相应的移动。

• 先进先出，与栈相反

优势：

• 规则固定，头部只能读取，插入只能在队尾进行，规则固定，可控性&安全性好。非常适合一些特殊业务场景

缺点：

• 只能从对头读取数据，不能从中间读取数据

典型场景：

• java线程池ThreadPoolExecutor，来不及处理的任务会临时放在任务队列中

• 各种MQ消息中间件，如：kafka、RocketMQ 等

5、哈希表

定义：

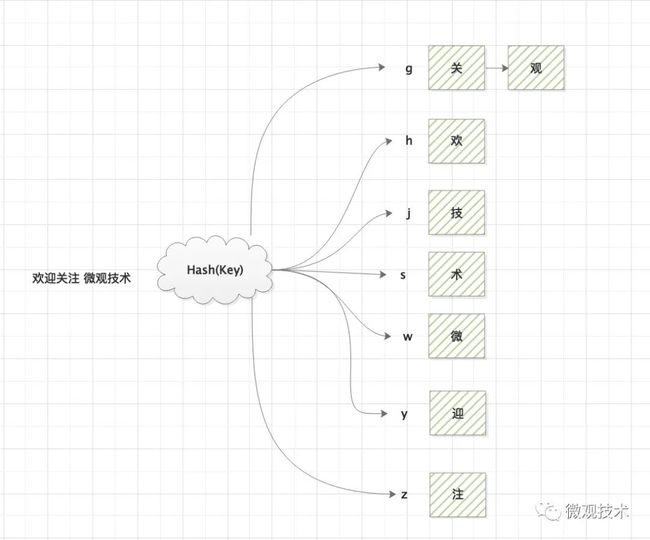
哈希表（Hash table）也叫散列表。根据键（Key）而直接访问在内存储存位置的数据结构。它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，加快查找速度。这个映射函数称为散列函数，存放记录的数组称做散列表。

划重点：

• Hash函数，建立key与value的映射关系。

• 常用的哈希函数有MD5、SHA、CRC等

优势：

• 分为治之，化大为小，降低了复杂度

• 通过key计算直接获取目标位置，提高查找速度

缺点：

可能存在哈希冲突，在每个冲突处构建链表，将所有冲突值链入链表。如果是恶意攻击，哈希表可能会退化为链表，所有元素都被存储在同一个节点的链表中，此时哈希表的查找速度=链表遍历查找速度=O(n)

为了描述冲突，引入装载因子=哈希表中的元素个数 / 哈希表长度，装载因子越大，说明链表的长度越长，性能会越低。

当装载因子过大时，需要动态扩容。申请一个更大的哈希表，将原哈希表的数据迁移到新的哈希表。

典型场景：

• Redis 数据库

• Java中的哈希表实现，HashMap

6、图

定义：

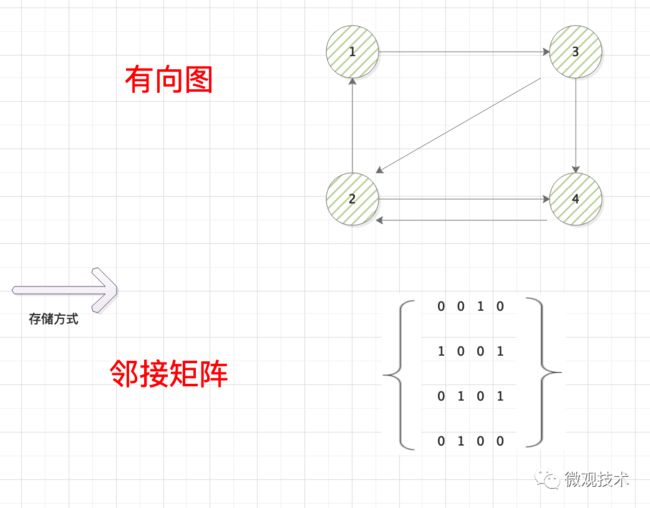
图(Graph)是由顶点的有穷非空集合和顶点之间的集合组成，通常表示为：G（V, E），其中 G 表示一个图，V 是图 G 中顶点的集合，E 是图 G 中边的集合。

上图是一个有向图G，G=（V，E），其中顶点集合 V = 1、2、3、4，边集合是 E = (1,3)、(2,1)、(2,4)、(3,2)、(3,4)、(4,2)

根据图是否有方向、权重等可以分为：有向图、无向图、带权图

划重点：

• 非线性表

• 任意两个节点关系

优势：

• 存储的信息完备

• 为任意两个顶点建立关系，称之为边。而树只能表示相邻两个节点的关系

缺点：

任意点都可以建立关系，所以数据量会比较大。为了便于存储，我们将图用多维数组表示，从而将很多图运算转换为矩阵运算。

当然，如果图比较稀疏的话，可以采用邻接表的存储方式，与哈希表类似，可以节省很多空间。

典型场景：

• 地图如何计算出最优出行路线

• 深度优先搜索

• 广度优先搜索

• 最小生成树

注意：

• 图主要有以下两种存储方式：

• 邻接矩阵。比较浪费空间，但是优点是查询效率高

• 邻接表。每个顶点对应一个链表，比较节省存储空间，但是查询效率会低些。当然为了提高查询效率，可以将里面的链表替换成红黑树、跳表、或者平衡二叉树。

7、树

定义：

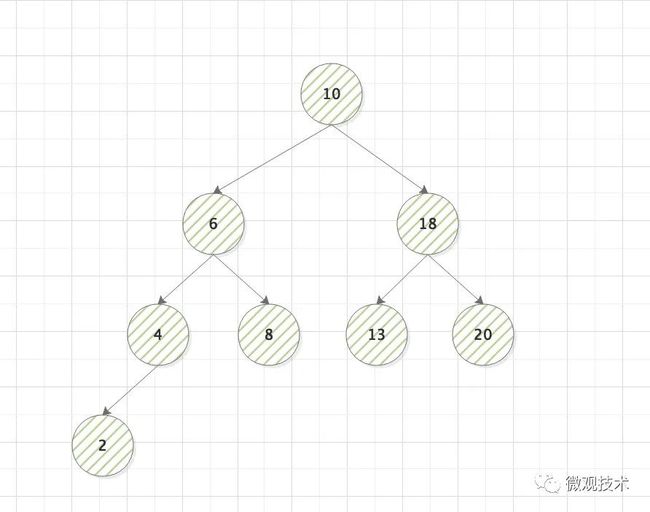
顾名思义，跟现实的树一样，树上的每一个元素成为节点，节点与节点之间有一定的关系，上下称为父子节点，左右称为兄弟节点。

按照树的表现结构，可以具体分为以下几种类型：二叉树、平衡二叉树、满二叉树、完全二叉树、递归树、红黑树、B- 树、B+ 树 ，等

划重点：

• 非线性结构

• 父子节点

• 兄弟节点

• 树型结构

• 每个节点包含3块信息：数据值、左右子节点指针。

优势：

• 树形结构，支持数据的快速插入、查找、删除

• 支持多种遍历方式：前序遍历、中序遍历、后序遍历

• 结构特殊，适合用递归来实现

缺点：

树中删除一个节点操作较复杂，需要根据其子节点的个数（0、1、2）分多种情况考虑，迁移部分节点，重新构造树结构。当然，也可以采用逻辑标记删除，物理空间没有释放，但会产生碎片，影响查询效率。

注意点：

• 红黑树出镜率很高，风头甚至盖过了平衡二叉树，因为红黑树只要求近似平衡，维护成本比AVL树要低，但性能损失不大。当HashMap中的链表数据较多时，也会将链表结构升级为红黑树结构。

• B+树主要是采用更加扁平的结构存储海量数据，降低树的深度，主要用在 mysql 数据库索引构建，有兴趣同学可以看下之前的文章

面试题：mysql 一棵 B+ 树能存多少条数据？

8、堆

定义：

一种特殊的二叉树。需要满足两个条件：1、是一棵完全二叉树 2、堆中每个节点的值必须>=或<=其左右子节点的值。

具体，根据每个节点的值是>= 还是 <= 子树中每个节点的值，分为大顶堆、小顶堆。

划重点：

• 节点的值要比左右子树的值大或小，只能一种选择

优势：

• 时间复杂度较低

• 获取堆顶元素的时间复杂度为 O(1)

• 假设完全二叉树包含n个节点，插入元素、删除元素，时间复杂度为 O(logn)

缺点：

• 特殊的二叉树

• 只能满足特殊的需求

典型场景：

• 堆排序

• 优先级队列

• 求 TOP K

• 求中位数

示例：从10亿个数据中找到最大的前10个？

• 假设10亿个数据存在数组中

• 取前10个数据，构建一个小顶堆，那么根节点是最小的

• 然后，从数组中依次取出一个数据与堆顶比较，如果大于，替换掉堆顶元素，堆内部调整；如果小于等于堆顶，不做处理

• 同样逻辑，依次循环处理数组中每一个元素。

• 当10亿个数据处理完后，堆中的数据就是Top 10

---

关于我：前阿里架构师，出过专利，竞赛拿过奖，CSDN博客专家，负责过电商交易、社区生鲜、营销、金融等业务，多年团队管理经验，爱思考，喜欢结交朋友