NumPy入门之线性代数

@[云好晕啊]学习笔记

线性代数

 线性代数是数学的一个分支，它的研究对象是向量，向量空间（或称线性空间），线性变换和有限维的线性方程组。向量空间是现代数学的一个重要课题；因而，线性代数被广泛地应用于抽象代数和泛函分析中。
 在NumPy中也有有关于线性代数计算的模块，也就是linalg模块，可以实现强大的线性代数计算，包括特征值、特征向量、矩阵分解等等。Numpy 定义了 matrix 类型，使用该 matrix 类型创建的是矩阵对象，它们的加减乘除运算缺省采 用矩阵方式计算，因此用法和Matlab十分类似。但是由于 NumPy 中同时存在 ndarray 和 matrix 对象，因此用户很容易将两者弄混。这有违 Python 的“显式优于隐式”的原则，因此官方并不推荐 在程序中使用 matrix 。在这里，我们仍然用 ndarray 来介绍。

---

矩阵和向量积

 因为矩阵的定义、矩阵加法、矩阵的数乘、矩阵的转置与二维数组完全一致，所以本章不再说明，但矩阵的乘法与二维数组是有不同的表示。

矩阵乘法

函数调用：

• numpy.dot(a,b[,out])
  

• 计算两个矩阵a、b的乘积，如果是一维数组则是他们的内积。
• 提醒：在线性代数里面讲的维数和数组的维数不同，如线性代数中提到的n维行向量在NumPy中是一维数组，而在线性代数中n维列向量在NumPy中是一个shape（n，1）的二维数组。

代码举例

import numpy as np

#矩阵和向量积
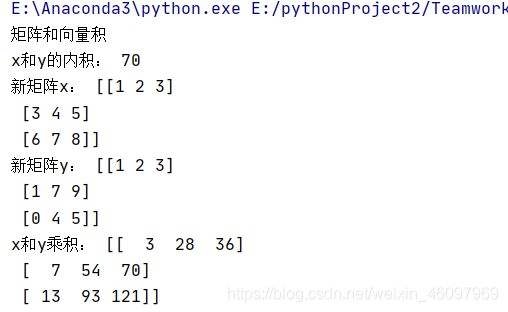
print('矩阵和向量积')
x=np.array([1,2,3,4,5])
y=np.array([2,3,4,5,6])
z=np.dot(x,y)
print('x和y的内积：',z)

x=np.array([[1,2,3],[3,4,5],[6,7,8]])
print('新矩阵x：',x)

y=np.array([[1,2,3],[1,7,9],[0,4,5]])
print('新矩阵y：',y)

z=np.dot(x,y)
print('x和y乘积：',z)

---

矩阵特征值和特征向量

 矩阵的特征向量是矩阵理论上的重要概念之一，它有着广泛的应用。数学上，线性变换的特征向量（本征向量）是一个非简并的向量，其方向在该变换下不变。该向量在此变换下缩放的比例称为其特征值（本征值）。
函数调用：

• numpy.linalg.eig(a)
  

• 计算方阵的特征值和特征向量

•   numpy.linalg.eigvalues(a)
  

• 计算方阵的特征值

代码举例

#矩阵特征值与特征向量
print('矩阵特征值与特征向量')
#创建一个对角矩阵
x=np.diag((1,2,3))
print('对角阵x：',x)
print('x特征值为：',np.linalg.eigvals(x))

a,b=np.linalg.eig(x)
#特征值保存在a中，特征向量保存在b中
print('特征值为：',a)
print('特征向量为：',b)

#检验特征值与特征向量是否正确
print('检验特征值与特征向量正确与否：')
for i in range(3):
    if np.allclose(a[i]*b[:,i],np.dot(x,b[:,i])):
        print('Right')
    else:
        print('False')
#判断矩阵是否为正定矩阵
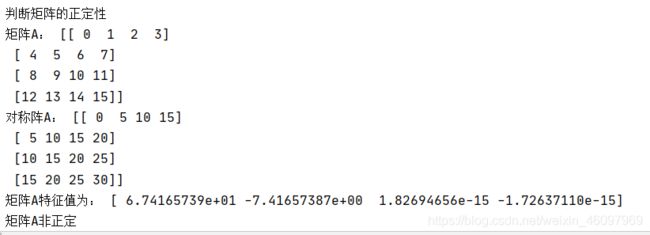
print('判断矩阵的正定性')
A=np.arange(16).reshape(4,4)
print('矩阵A：',A)

#将方阵转为对称阵
A=A+A.T
print('对称阵A：',A)

B=np.linalg.eigvals(A)
#计算A的特征值
print('矩阵A特征值为：',B)
#正定判断，即每个特征值都大于0使用all函数
if np.all(B>0):
    print('矩阵A正定')
else:
    print('矩阵A非正定')

---

矩阵分解

3.1 奇异值分解

有关于奇异值分解的原理这里不一一赘述，可以参考如下：奇异值分解(SVD)及其应用
函数调用：

• u,s,v=numpy.linalg.svd(a,full_matrices=True,compute_uv=True,hermitian=False)
  

• a是一个形如（M,N)的矩阵
• full_matrices取值是为False或者True，默认值为True，这时候u的大小为(M,M),v的大小为(N,N)。否则u的大小为(M,K),v的大小为(K,N),K=min(M,N)。
• compute_uv取值为False或者True，默认为True，表示计算u,s,v。为False的时候只计算s。
• 总共三个返回值u,s,v，u大小为(M,M)，s大小为(M,N),v大小为(N,N)，a=usv。
• 其中s是对矩阵a的奇异值分解。s除了对角元素不为0外，其余元素都为0，并且对角元素从大到小排列。s中有n个奇异值，一般排在后面的比较接近0，所以仅保留比较大的r个奇异值。
• 注：NumPy中返回的v是通常所谓奇异值分解a=usv中v的转置。

示例代码

import numpy as np

#矩阵分解
#奇异值分解
print('奇异值分解1')
A=np.array([[1,1],[1,-2],[2,1]])
print('用于奇异值分解的矩阵A：',A)

u,s,vh=np.linalg.svd(A,full_matrices=False)
print('左奇异阵大小：',u.shape)
print('相应对角阵:',np.diag(s))

print('右奇异矩阵大小：',vh.shape)
print('右奇异矩阵：',vh)

a=np.dot(u,np.diag(s))
a=np.dot(a,vh)
print('奇异值分解后再组合形成矩阵：',a)

print('奇异值分解2')
A=np.array([[4,11,14],[8,7,-2]])
print('用于奇异值分解的矩阵A：',A)

u,s,vh=np.linalg.svd(A,full_matrices=False)
print('左奇异阵大小：',u.shape)
print('相应对角阵:',np.diag(s))

print('右奇异矩阵大小：',vh.shape)
print('右奇异矩阵：',vh)

a=np.dot(u,np.diag(s))
a=np.dot(a,vh)
print('奇异值分解后再组合形成矩阵：',a)

3.2 QR分解

有关QR分解原理：QR分解

函数调用：

• q,r=numpy.linalg.qr(a,mode='reduced')
  

• 此函数用于计算矩阵a的QR分解
• a是一个(M,N)的待分解矩阵
• mode=reduced:返回(M,N)的列向量两两正交的矩阵q，和(M,N)的三角阵r（Reduced QR分解）
• mode=complete:返回(M,M)的正交矩阵q，和(N,N)的三角阵r（Full QR分解）

代码示例

print('QR分解1')
A=np.array([[2,-2,3],[1,1,1],[1,3,-1]])
print('QR分解矩阵A：',A)
q,r=np.linalg.qr(A)
print('q矩阵大小：',q.shape)
print('q:',q)

print('r矩阵大小：',r.shape)
print('r:',r)

print('q*r:',np.dot(q,r))

a=np.allclose(np.dot(q.T,q),np.eye(3))
print('q是否正交：',a)

print('QR分解2')
A=np.array([[1,1],[1,-2],[2,1]])
print('QR分解矩阵A：',A)
q,r=np.linalg.qr(A,mode='complete')
print('q矩阵大小：',q.shape)
print('q:',q)

print('r矩阵大小：',r.shape)
print('r:',r)

print('q*r:',np.dot(q,r))

a=np.allclose(np.dot(q.T,q),np.eye(3))
print('q是否正交：',a)

3.3 Cholesky分解

 有关Cholesky分解原理：Cholesky分解原理

函数调用：

• L=numpy.linalg.cholesky(a)
  

• 函数返回正定矩阵kbd>a的Cholesky分解kbd>a=L*L.T,其中L是下三角

代码示例

#Cholesky分解
print('Cholesky分解')
A=np.array([[1,1,1,1],[1,3,3,3],[1,3,5,5],[1,3,5,7]])
print('用于分解的矩阵A：',A)
print('A矩阵特征值：',np.linalg.eigvals(A))
L=np.linalg.cholesky(A)
print('Cholesky分解结果:',L)
print('重构：',np.dot(L,L.T))

---

范数和其他数字

4.1 矩阵的范数

一个在 m*n的矩阵上的矩阵范数(matrix norm)是一个从 线性空间到实数域上的一个函数，记为|| ||，它对于任意的 m*n矩阵A和B及所有实数a，满足以下四条性质：

1. ||A||>=0;
2. ||A||=0 iff A=O （零矩阵）; （1和2可统称为正定性）
3. ||aA||=|a| ||A||; （齐次性）
4. ||A+B||<= ||A|| + ||B||. （三角不等式）
   

函数调用：

• numpy.linalg.norm(x,ord=None,axis=None,keepdims=False)
  

• 该函数用于计算向量或者矩阵的范数
• x是一个向量或矩阵
• axis：指定轴，0表示沿列，1表示沿行，不指定表示整个数组或矩阵。
• keepdims:接收boolean，可选。如果将其设置为True，则将缩小的轴作为尺寸为1的尺寸留在结果中。使用此选项，结果将在输入数组中正确广播。
• ord参数的不同，计算的范数也不同
  

示例代码

（1）求向量的范数

import numpy as np

#矩阵的范数
print('求向量的范数')
x=np.array([1,2,3,4])

print('和最大值，按列',np.linalg.norm(x,ord=1))#最大值，按列
print('和最大值，按列：',np.sum(np.abs(x)))

print('2范数:',np.linalg.norm(x,ord=2))
print('2范数：',np.sum(np.abs(x)**2)**0.5)

print('和最小值，按行',np.linalg.norm(x,ord=-np.inf))
print('和最小值，按行',np.min(np.abs(x)))

print('和最大值，按行：',np.linalg.norm(x,ord=np.inf))
print('和最大值，按行：',np.max(np.abs(x)))

（2）求矩阵的范数

print('求矩阵的范数')
A=np.array([[1,2,3,4],[2,3,5,8],[1,3,5,7],[3,4,7,11]])
print('矩阵A：',A)

print('和最大值，按列',np.linalg.norm(A,ord=1))#最大值，按列
print('和最大值，按列：',np.sum(np.abs(A),axis=0))

print('2范数:',np.linalg.norm(A,ord=2))
print('2范数：',np.max(np.linalg.svd(A,compute_uv=False)))

print('按行计算和的最大值：',np.linalg.norm(A,ord=np.inf))
print('按行计算和的最大值：',np.max(np.sum(A,axis=1)))

print('fro:',np.linalg.norm(A,ord='fro'))
print('frp:',np.trace(np.dot(A.T,A)))

4.2 方阵的行列式

 行列式可以看做是有向面积或体积的概念在一般的欧几里得空间中的推广。或者说，在 n 维欧几里得空间中，行列式描述的是一个线性变换对“体积”所造成的影响。
函数调用：

•  numpy.linalg.det(a)
  

• a:用于计算行列式的方阵

代码示例

（1）计算行列式

#方阵的行列式
print('方阵的行列式')
x=np.array([[1,2],[3,4]])
print('用于计算的矩阵：',x)

print('行列式结果:',np.linalg.det(x))

4.3 矩阵的秩

 一个矩阵A的列秩是A的线性独立的纵列的极大数，通常表示为r(A)，rk(A)或rank A。
函数调用：

•  numpy.linalg.matric_rank(M,tol=None,hermitian=False)
  

• 函数返回矩阵的秩
• M：要计算秩的矩阵M
• tol：默认为空。低于此阈值，SVD值被视为零。
• hermitian：boolean，默认为False。如果为真，“M”假定为Hermitian（实值为对称），启用更有效的方法来查找奇异值。

示例代码

#矩阵的秩
I=np.eye(3)
print('单位阵：',I)
r=np.linalg.matrix_rank(I)
print('矩阵的秩:',r)

I[1,1]=0
print('新的I：',I)

r=np.linalg.matrix_rank(I)
print('I矩阵的秩：',r)

4.4 矩阵的迹

 在线性代数中，一个n×n矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数），一般记作tr(A)。
函数调用：

• numpy.trace(a,offset=0,axis1=0,axis2=1,dtype=None,out=None)
  

• a：用于计算迹的矩阵
• offset:接收int类型，对角线与主对角线的偏移。两者都可以是积极的，默认为0。
• axis1 axis2:作为第一个子轴的第二个子轴数组从中取对角线。默认值是a的前两个轴值。
• dtype：指定输入矩阵值得类型。
• out：接收ndarray，表示将结果存入指定数组类型。

代码举例

（1）计算方阵的迹

#矩阵的迹
print('矩阵的迹')
x=np.array([[1,2,3],[4,5,6],[7,8,9]])
print('矩阵x:',x)

y=np.array([[5,4,2],[1,7,9],[0,4,5]])
print('矩阵y：',y)

print('矩阵x的迹：',np.trace(x))
print('矩阵x转置的迹：',np.trace(np.transpose(x)))
print('x，y两者和的迹',np.trace(x+y))#和的迹等于迹的和
print('x，y两者迹的和',np.trace(x)+np.trace(y))

---

解方程和逆矩阵

5.1 逆矩阵（inverse matrix）

 设 A 是数域上的一个 n 阶矩阵，若在相同数域上存在另一个 n 阶矩阵 B，使得： AB=BA=E （E 为单 位矩阵），则我们称 B 是 A 的逆矩阵，而 A 则被称为可逆矩阵。
函数调用：

•  numpy.linalg.inv(a)
  

• 函数返回矩阵的逆矩阵（矩阵可逆虫咬条件是det(a) != 0不为0，或者a满秩）。
• a：用于计算逆矩阵的矩阵

代码示例

import numpy as np

#计算逆矩阵
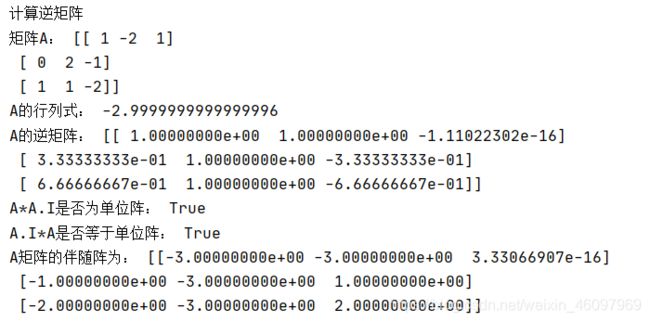
print('计算逆矩阵')
A=np.array([[1,-2,1],[0,2,-1],[1,1,-2]])
print('矩阵A：',A)

#计算A的行列式判断是否可逆
A_det=np.linalg.det(A)
print('A的行列式：',A_det)

#求A得逆矩阵
A_inverse=np.linalg.inv(A)
print('A的逆矩阵：',A_inverse)

x=np.allclose(np.dot(A,A_inverse),np.eye(3))
print('A*A.I是否为单位阵：',x)
x=np.allclose(np.dot(A_inverse,A),np.eye(3))
print('A.I*A是否等于单位阵：',x)

#计算伴随阵
A_companion=A_inverse*A_det
print('A矩阵的伴随阵为：',A_companion)

5.2 求解线性方程组

 线性方程组是各个方程关于未知量均为一次的方程组(例如2元1次方程组）。附链接：线性方程组
函数调用：

• numpy.linalg.solve(a,b)
  

• 函数返回线性方程组或矩阵方程的解
• a：线性方程系数矩阵
• b：线性方程结果，列向量或矩阵

代码示例

#解线性方程组
print('解线性方程组')
A=np.array([[1,2,1],[2,-1,3],[3,1,2]])
b=np.array([7,7,18])
x=np.linalg.solve(A,b)
print('线性方程组解法1：',x)

#A.I*b
x=np.linalg.inv(A).dot(b)
print('线性方程组解法2：',x)

y=np.allclose(np.dot(A,x),b)
print('解是否正确：',y)

---

总结

 线性方程对于工科学习的重要性不言而喻，所以数据分析中掌握好NumPy模块中有关于线性方程相关函数的如何调用也十分重要。