使用statsmodels实现线性回归

statsmodels简介

Statsmodels 是 Python 中一个强大的统计分析包，包含了回归分析、时间序列分析、假设检
验等等的功能。Statsmodels 在计量的简便性上是远远不及 Stata 等软件的，但它的优点在于可以与 Python 的其他的任务（如 NumPy、Pandas）有效结合，提高工作效率。在此，重点介绍最回归分析中最常用的 OLS（ordinary least square）功能。

当你需要在 Python 中进行回归分析时……
import statsmodels.api as sm！！！

关于统计模型

statsmodels是一个Python软件包，为scipy提供了补充，以进行统计计算，包括描述性统计以及统计模型的估计和推断。

statsmodels主要包括如下子模块：

回归模型：线性回归，广义线性模型，稳健的线性模型，线性混合效应模型等等。

方差分析（ANOVA）。

时间序列分析：AR，ARMA，ARIMA，VAR和其它模型。

非参数方法： 核密度估计，核回归。

统计模型结果可视化。

比较：statsmodels更关注统计推断，提供不确定估计和参数p-value。相反的，scikit-learn注重预测。

主要特点

线性回归模型：

普通最小二乘法
广义最小二乘法
加权最小二乘法
具有自回归误差的最小二乘
分位数回归
递归最小二乘法

具有混合效应和方差成分的混合线性模型
GLM：支持所有单参数指数族分布的广义线性模型
用于二项式和泊松的贝叶斯混合GLM
GEE：单向聚类或纵向数据的广义估计方程

离散模型:

Logit 和 Probit
多项 logit (MNLogit)
泊松和广义泊松回归
负二项式回归
零膨胀计数模型

RLM: 鲁棒的线性模型，支持多个 M 估计器。

时间序列分析：时间序列分析模型
完整的StateSpace建模框架
季节性ARIMA和ARIMAX模型
VARMA和VARMAX模型
动态因子模型
未观测到的组件模型

马尔可夫切换模型（MSAR），也称为隐马尔可夫模型（HMM）

单变量时间序列分析：AR，ARIMA
矢量自回归模型，VAR和结构VAR
矢量误差修正模型，VECM
指数平滑，Holt-Winters
时间序列的假设检验：单位根，协整和其他
用于时间序列分析的描述性统计数据和过程模型

生存分析:

比例风险回归（Cox模型）
生存者函数估计（Kaplan-Meier）
累积发生率函数估计

多变量:

缺失数据的主成分分析
旋转因子分析
MANOVA
典型相关

非参数统计：单变量和多变量核密度估计

数据集：用于示例和测试的数据集
统计：广泛的统计检验
诊断和规格检验
拟合优度和正态性检验
多元测试函数
各种其他统计检验

其他模型

Sandbox：statsmodels包含一个 sandbox 文件夹，其中包含处于开发和测试各个阶段的代码， 因此不被视为“生产就绪”。其中包括：
广义矩法（GMM）估计器
核回归
scipy.stats.distributions的各种扩展
面板数据模型
信息理论测度

什么是线性回归？

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。

在回归术语中，我们将被预测的变量称为因变量(dependent variable)，用y表示。把用来预测应变量值的一个或多个变量称为自变量（predictor variable/independent variable），用x表示。

简单线性回归案例

数据集说明

本文用于分析的样本数据集手动定义，有利于结果一目了然，特别容易理解。

导入需要的工具包

import statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.sandbox.regression.predstd import wls_prediction_std
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("darkgrid")
import pandas as pd

如果电脑上面没有安装这些包，直接下载速度过慢，可以选择在国内的网站上面下载安装。

pip install statsmodels -i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com
pip install matplotlib -i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com
pip install seaborn -i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com
pip install pandas -i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com 

使用pandas生成数据

自定义的数据，可任意修改。注意：列名中，相当于把“a”列作为主键，让两个数据集可以关联起来。

a = pd.DataFrame([[1,2,20,4,5],
                  [2,3,21.2,34,45],
                  [3,4,22.1,34,45],
                  [4,5,22.9,34,45],
                  [5,6,24.1,34,46]],index=['1','2','3','4','5'],columns=list('aBCDE'))
print(a)
b = pd.DataFrame([[1,22,33,44,55],
                  [2, 'b42', 'b43', 'b44', 65.1],
                  [3, 'b42', 'b43', 'b44', 75.3],
                  [4, 'b42', 'b43', 'b44', 85],
                  [5, 'b52', 'b53', 'b54', 95.8]],index=list('12345'),columns=list('abcde'))
print(b)

输出结果（了解数据样式）：

数据整理

我们现在已经成功生成了数据，使用Pandas的merge函数，将多个表格合并为一张总表格，以便数据分析。

#相当于sql中的join on 连接数据
df = a.merge(b,on="a")
#显示前十行数据，因为只有五条，所以相当于把数据全部显示
print(df.head(10))
df.to_csv("./df.csv")

输出结果（了解数据样式）：

回归模型

简单线性回归使用一个自变量来预测一个因变量，二者之间的关系可以用一条直线近似表示。

简单线性回归模型： y = a + bx +c

其中：

y = 因变量

b = 回归系数

a = 截距 （自变量为0时，因变量房价的平均值/期望）

x = 用于预测y的自变量

c = 随机变量，称为模型误差项，说明在y里面但不能被x和y之间线性关系解释的变异性

建模

我们将使用statsmodels中ols功能，构建B同e之间的模型。

Statsmodels是一个很强大的Python库，用于拟合多种统计模型，执行统计测试以及数据探索和可视化。

对于线性回归linear regression，我们可以使用Statsmodels库中最小二乘法OLS（Ordinary-Least-Square）的功能来实现，可以得到丰富的数据信息。

model = ols("B ~ e",data=df).fit()
model_summary = model.summary()

print(model_summary)

结果：

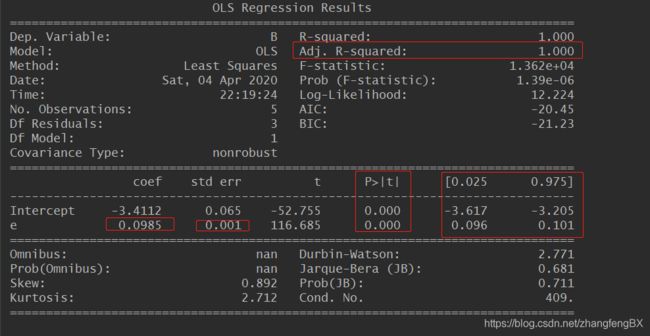
1） 修正判定系统Adj.R-squared：100.00%。自定义数据指数变异性的100.00%能被其与“a”列数据之间的线性关系解释。

2）回归系数：0.0985。代表c列数值增加1个单位，a列数值将增加0.0985。和我们自定义的数据是符合的，差不多“e”列数据步长差不多是“a”列的10倍。

3）回归系数的标准误差stand error：0.001，即b的估计的标准差。通过不同的数据，可以计算得到回归系统的标准误差。回归系数标准误差，是量度结果精密度的指标。这里计算得出的标准误差为0.001，数值非常小，说明精确度是相当高的。
如果自定义数据比较离散，这个值会增大。

4）p>|t| 值为0%。根据简单线性回归显著性的t检验，原假设“a”列与“e”列之间不存在线性关系，b为0。
而现在p值为0%，小于显著性水平0.05。所以拒绝原假设，b显著不等于0。我们足以断定，“a”列与“e”列之间存在一个显著的关系。

5）b的95%的置信区间：0.096 ~ 0.101。我们有95%的信心，回归系数b将落在置信区间 [0.096,0.101]中。换个角度来讲，简单线性回归显著性的t检验，假设b为0，而b=0并没有包含在上述置信区间内，所以我们可以拒绝原假设，断定“a”列与“e”列之间存在一个显著的关系。

关于自变量的线性回归图像

fig = plt.figure(figsize=(15,8))
fig = sm.graphics.plot_regress_exog(model,"e",fig=fig)
plt.show()
#也可以把图片保存到本地，使用下面方法
#fig.savefig('./test.jpg', dpi=300)

图片显示如下：

图像说明：

1）左上一图 “Y and Fitted vs. X” ，刻画了“a”列与“e”列同线性回归模型拟合的估计值之间的差距。同时，可以发现二者是正相关的，斜率β为负。

2）右上一图 “Residuals versus e”为 关于自变量“e”的残差图。横坐标为自变量“e”的值，纵轴表示自变量对应的残差值，也就是左上一图中蓝圆点同橘色菱形间的距离差。
残差图是用来评价回归模型假定有效性的一种方法。通过这张残差图，总体印象为所有的散点都在±0.04范围的水平带中间，我们有信心做出结论，简单线性回归模型是合理的。 （残差图，直线上下的点分布均匀且都在之间附近，效果越好）

3）左下一图“Partial regression plot”偏回归图像显示考虑新增其他自变量时，“a”列与“e”列之间的关系。 在多元线性回归当中，可以增加更多的自变量后同样的图像将产生怎样的变化。

4）右下二图“ （CCPR Plot）”图像是偏回归图像的拓展，反映了考虑新增其他自变量后反应两者关系的直线将如何变化。
现在这个是加了一个新变量c且值为3。可以理解线性回归模型变成下面这样：
简单线性回归模型： y = a + bx + 3

置信区间

下面我们做图画出拟合线（绿色标记），样本数据中的观测值（蓝色圆点），置信区间（红色标记）。

# x为自变量，y为因变量
# 注意单个方括号为series，两个方括号为dataframe
x=df[["e"]]
y=df[["B"]]

xxx,lower,upper = wls_prediction_std(model)
fig,ax = plt.subplots(figsize=(10,7))
ax.plot(x,y,'o',label="a")
ax.plot(x,model.fittedvalues,"g--",label="OLS")
ax.plot(x,upper,"r--")
ax.plot(x,lower,"r--")
ax.legend(loc="best")
plt.show()

结果如下如：

完整代码

不想敲代码的，直接复制下面

import statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.sandbox.regression.predstd import wls_prediction_std
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("darkgrid")
import pandas as pd

# a = pd.DataFrame(np.random.randn(4,5),index=[1,2,3,4 ],columns=list('abcde'))
a = pd.DataFrame([[1,2,20,4,5],
                  [2,3,21.2,34,45],
                  [3,4,22.1,34,45],
                  [4,5,22.9,34,45],
                  [5,6,24.1,34,46]],index=['1','2','3','4','5'],columns=list('aBCDE'))
print(a)
# b = pd.DataFrame({"a":pd.Series(np.random.randn(4),index=['b','c','d','e']),
#                   "two":pd.Series(np.random.randn(2),index=['b','c']),
#                   "three":pd.Series(np.random.randn(3),index=['b','c','d'])})
b = pd.DataFrame([[1,22,33,44,55],
                  [2, 'b42', 'b43', 'b44', 65.1],
                  [3, 'b42', 'b43', 'b44', 75.3],
                  [4, 'b42', 'b43', 'b44', 85],
                  [5, 'b52', 'b53', 'b54', 95.8]],index=list('12345'),columns=list('abcde'))
print(b)
#相当于sql中的join on 连接数据
df = a.merge(b,on="a")
print(df.head(10))
df.to_csv("./df.csv")
# df.info()

model = ols("B ~ e",data=df).fit()
model_summary = model.summary()

print(model_summary)

fig = plt.figure(figsize=(15,8))
fig = sm.graphics.plot_regress_exog(model,"e",fig=fig)
plt.show()

# x为自变量，y为因变量
# 注意单个方括号为series，两个方括号为dataframe
x=df[["e"]]
y=df[["B"]]

xxx,lower,upper = wls_prediction_std(model)
fig,ax = plt.subplots(figsize=(10,7))
ax.plot(x,y,'o',label="a")
ax.plot(x,model.fittedvalues,"g--",label="OLS")
ax.plot(x,upper,"r--")
ax.plot(x,lower,"r--")
ax.legend(loc="best")
plt.show()