【写在前面】
“Java算法系列”目录如下(更新ing):
- 数据结构相关算法
- 八大排序算法:冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、基数排序、堆排序
- 四大查找算法:线性查找、二分查找、插值查找、斐波那契查找
- 九大常用算法:分治算法、动态规划算法、KMP算法、贪心算法、Prim算法、Kruskal算法、Dijkstra算法、Floyd算法、骑士周游回溯算法
本篇为九大常用算法之动态规划算法。
〇、基本介绍
动态规划算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法。
动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。动态规划算法对于下一个子阶段的求解,是建立在上一个子阶段的解的基础上进行进一步的求解。
动态规划和贪心算法一样,是求最优解的一种思想方法,可以通过填表的方式来逐步推进,得到最优解。
为方便做题,可将动态规划不严格地分为四类:线性动态规划、二维动态规划、树形动态规划、背包问题。
牛客网动态规划专项将动态规划分成了九类:线性dp、前缀和、差分、二维dp、背包、区间dp、树形dp、状压dp、数位dp。
本文将介绍线性动态规划、二维动态规划、背包问题等三类。
1 线性动态规划
1.1 斐波那契数列问题
要求输入一个正整数 n ,请你输出斐波那契数列的第 n 项。
本例见:牛客网NC65 斐波那契数列
回顾经典的“斐波那契数列问题”,斐波那契数可以用两个初始条件和一个简单的递推式来定义:
$$ F(n)= \begin{cases} 0, &n=0\\ 1, &n=1\\ F(n-1) + F(n-2), &n>1 \end{cases} $$
除了使用递归的方法求解,也可以使用非递归的方法。
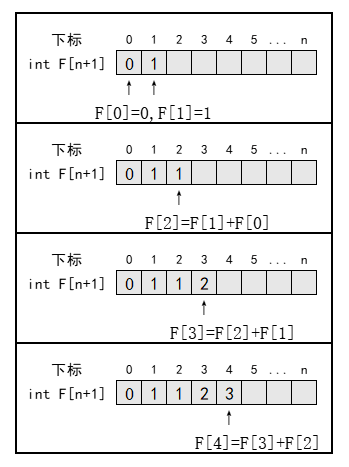
对于 F(n) 的求解可以计算它的两个更小的交叠子问题 F(n-1) 和 F(n-2),因此可以在一张一维表中填入 n+1 个 F(n) 的连续值:
代码如下:
public class Solution {
public int Fibonacci(int n) {
if (n <= 1) return n;
int[] F = new int[n + 1];
F[0] = 0;
F[1] = 1;
for (int i = 2; i <= n; i++) {
F[i] = F[i - 1] + F[i - 2];
}
return F[n];
}
}动态规划算法可以解释为一种空间换时间的权衡技术。不过在“斐波那契数列问题”中,可以对动态规划再作改进,则可避免使用额外的空间,这里不赘述。
1.2 币值最大化问题
给定一排n个硬币,其面值均为正整数 C1, C2, …, Cn,这些整数并不一定两两不同。请问如何选择硬币,使得在其原始位置互不相邻的条件下,所选硬币的总金额最大。
本例可参考:NC2 不相邻取数
如何选择硬币呢?对于前 n 枚硬币的最大可选金额设为 F(n)。对于第 n 枚硬币(n≥2),事实上有两种情况:
- 不选择第 n 枚硬币,则前 n 枚硬币的最大可选金额与前 n-1 枚硬币的最大可选金额一致,即:F(n) = F(n-1)
- 选择第 n 枚硬币,则第 n-1 枚硬币一定不可选,前 n 枚硬币的最大可选金额为第 n 枚再加上前 n-2 枚硬币:F(n) = Cn + F(n-2)
到底该选择这两种情况的哪一种呢?两种情况取最大值即可。因此可以得到递推公式:
$$ F(n)= \begin{cases} 0, &n=0\\ C_1, &n=1\\ max\{ F(n-1),C_n + F(n-2) \}, &n>1 \end{cases} $$
以一排硬币{5, 1, 2, 10, 6, 2}为例,填表过程如下:
前6枚硬币的最大可选金额即所求,故一排硬币{5, 1, 2, 10, 6, 2}的最大可选金额为17。
建一维表时,如币值数组为 C[n] ,则动态规划数组应为 F[n + 1] 。
币值最大化问题的代码如下:
public class Solution {
//输入:数组C[0..n-1]保存n个硬币的面值
public int CoinRow(int[] C) {
int n = C.length;
if (n == 0) return 0;
if (n == 1) return C[0];
int[] F = new int[n + 1];
F[0] = 0;
F[1] = C[0];
for (int i = 2; i <= n; i++) {
F[i] = Math.max(F[i - 1], C[i - 1] + F[i - 2]);
}
return F[n];
}
}但是,以上填表过程仅仅得出最优解的值,并没有给出最优解的方案。要求出最优解选择了哪些硬币,需要回溯上述计算过程。如何回溯呢?下文“01背包问题”将作为列举回溯过程的例子,其思想是一样的。
1.3 不相邻取数问题
牛客网动态规划专题的“不相邻取数问题”与币值最大化问题几乎一致:
第一行输入一个正整数n,代表数组长度。第二行输入n个正整数,代表整个数组。输出不相邻的数的最大和。
本例见:NC2 不相邻取数
这里贴一个我的解法:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long n = sc.nextLong();
long[] C = new long[(int) n];
for (int i = 0; i < n; i++) {
C[i] = sc.nextInt();
}
if (n == 0) {
System.out.print(0);
return;
}
if (n == 1) {
System.out.print(C[0]);
return;
}
long[] F = new long[(int) n + 1];
F[0] = 0;
F[1] = C[0];
for (long i = 2; i <= n; i++) {
F[(int) i] = Math.max(F[(int) i - 1], C[(int) i - 1] + F[(int) i - 2]);
}
System.out.print(F[(int) n]);
}
}1.4 找零问题
与币值最大化问题类似的,还有找零问题:
需找零金额为n,最少要用多少面值为 d1 < d2 < … < dn 的硬币?
这里贴个伪代码,不赘述:
2 二维动态规划问题
2.1 硬币收集问题
在 n×m 格木板中放有一些硬币,每格的硬币数目最多为一个。在木板左上方的一个机器人需要收集尽可能多的硬币并把它们带到右下方的单元格。每一步,机器人可以从当前的位置向右移动一格或向下移动一格。设计一个算法找出机器人能找到的最大硬币数。
本例可参考:NC9 字母收集
设第 i 行第 j 列的格子能收集的最大硬币数为 F( i , j )。如何到达第 i 行第 j 列这个格子呢?有以下两种情况:
- 从上方单元格( i-1 , j )到达。
- 从左方单元格( i , j-1 )到达。
到底该选择这两种情况的哪一种呢?两种情况取最大值即可。此外,还需要加上当前格子的硬币数 Cij。因此可以得到递推公式:
$$ F(i,j)= \begin{cases} 0, & i=0, j=0 \\ 0, & i=0, 1 \le j \le m\\ 0, & j=0, 1 \le i \le n\\ max\{ F(i-1,j),F(i,j-1) \} + C_{ij}, & 1 \le i \le n, 1 \le j \le m \end{cases} $$
以下图为例:
填表过程如下:
建二维表时,如硬币数组为 C[n][m] ,则动态规划数组应为 F[n+1][m+1] 。
先初始化第0行、第0列为0,再按照递推公式填表即可。
填表时,既可以逐行填写,也可以逐列填写。为与以下代码保持一致,上图是逐行进行填写的。
所谓动态规划算法,即这个填表过程的模拟:
public class Solution {
public static void main(String[] args) {
int[][] C = {{0, 0, 0, 0, 1, 0},
{0, 1, 0, 1, 0, 0},
{0, 0, 0, 1, 0, 1},
{0, 0, 1, 0, 0, 1},
{1, 0, 0, 0, 1, 0}};
System.out.println("收集的最大硬币数为: " + coinCollection(C));
}
public static int coinCollection(int[][] C) {
int n = C.length;
int m = C[0].length;
int[][] dp = new int[n + 1][m + 1];
// 不需要初始化dp数组的第0行、第0列,因为Java的int数组默认值就是0
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 图解中下标从1开始,代码中下标从0开始,故为C[i-1][j-1]
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + C[i - 1][j - 1];
}
}
return dp[n][m];
}
}同样的,以上填表过程仅仅得出最优解的值,并没有给出最优解的路径。
2.2 字母收集问题
与硬币收集问题类似的,还有牛客网动态规划专题的“字母收集问题”:
有一个n×m的矩形方阵,每个格子上面写了一个小写字母。小红站在矩形的左上角,她每次可以向右或者向下走,走到某个格子上就可以收集这个格子的字母。
小红非常喜欢 "love" 这四个字母。她拿到一个 l 字母可以得 4 分,拿到一个 o 字母可以得 3 分,拿到一个 v 字母可以得 2 分,拿到一个 e 字母可以得 1 分。
她想知道,在最优的选择一条路径的情况下,她最多能获取多少分?本例见:NC9 字母收集
这里贴一个我的解法:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
char[][] C = new char[n][m];
for (int i = 0; i < n; i++) {
String s = sc.next();
for (int j = 0; j < m; j++) {
C[i][j] = s.charAt(j);
}
}
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + score(C[i - 1][j - 1]);
}
}
System.out.print(dp[n][m]);
}
public static int score(char ch) {
if (ch == 'l') return 4;
else if (ch == 'o') return 3;
else if (ch == 'v') return 2;
else if (ch == 'e') return 1;
else return 0;
}
}3 背包问题
由于篇幅有限,背包问题请看这里:【Java算法系列】背包问题
强烈建议阅读这篇背包问题!