数据统计与分析实验四:机器学习算法建模与求解(R语言,还没写完)
数据统计与分析实验四:机器学习算法建模与求解(R语言)
-
-
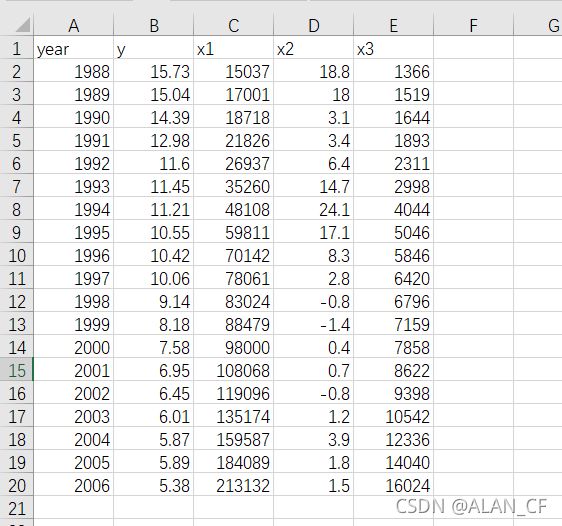
- 1、对于下表中的数据,对1990年-2006年内的数据建立人口自然增长率对于国民总收入、CPI增长率和人均GDP的三元线性回归模型。
-
- 1.1 手动输入数据到csv文件
- 1.2 导入数据、检查数据、建立多元线性回归统计模型
- 1.3 显著性检验
- 1.4 残差分析(我不是特别理解含义)
- 1.5 拿1988-2006的模型预测2020,发现与实际的2020的人口自然增长率不符(毕竟数据老了很多)
- 2、下载UCI中wine数据集:http://archive.ics.uci.edu/ml/datasets/Wine。所下载数据可以用txt打开,其中每一行数据为一种Wine的记录,每条记录包含14个维度,其中第一维为该Wine类别,后面13维为具体的Wine属性。请基于所有的178个Wine样本对Wine的13个维度进行PCA降维分析,将贡献率之和大于90%的成分提取,并将原13维属性数据映射为新数据。
- 3、聚类分析
-
- (1)随机生成均值、方差各不相同,且相互之间有少量交叉的3个类,每类30个样本,用不同的颜色进行展示。
- (2)通过keamns聚类分析,将所有的数据分成3类、4类、5类,每一类用不同颜色展示。
- 4、随机生成完全不交叉的2个类,每个类包含30个样本,用SVM进行分类和返回所有支撑向量,并以合适方式进行Figure展示。
-
1、对于下表中的数据,对1990年-2006年内的数据建立人口自然增长率对于国民总收入、CPI增长率和人均GDP的三元线性回归模型。
1.1 手动输入数据到csv文件
1.2 导入数据、检查数据、建立多元线性回归统计模型
> Data<-read.csv("E:\\CODING__ALAN_CF\\R_programLanguage\\data_4-1.csv")#从csv文件导入数据
> Data #检查数据
year y x1 x2 x3
1 1988 15.73 15037 18.8 1366
2 1989 15.04 17001 18.0 1519
3 1990 14.39 18718 3.1 1644
4 1991 12.98 21826 3.4 1893
5 1992 11.60 26937 6.4 2311
6 1993 11.45 35260 14.7 2998
7 1994 11.21 48108 24.1 4044
8 1995 10.55 59811 17.1 5046
9 1996 10.42 70142 8.3 5846
10 1997 10.06 78061 2.8 6420
11 1998 9.14 83024 -0.8 6796
12 1999 8.18 88479 -1.4 7159
13 2000 7.58 98000 0.4 7858
14 2001 6.95 108068 0.7 8622
15 2002 6.45 119096 -0.8 9398
16 2003 6.01 135174 1.2 10542
17 2004 5.87 159587 3.9 12336
18 2005 5.89 184089 1.8 14040
19 2006 5.38 213132 1.5 16024
> Data$year
[1] 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
[19] 2006
> Data$y
[1] 15.73 15.04 14.39 12.98 11.60 11.45 11.21 10.55 10.42 10.06 9.14 8.18 7.58 6.95 6.45
[16] 6.01 5.87 5.89 5.38
> Data$x1
[1] 15037 17001 18718 21826 26937 35260 48108 59811 70142 78061 83024 88479 98000
[14] 108068 119096 135174 159587 184089 213132
> Data$x2
[1] 18.8 18.0 3.1 3.4 6.4 14.7 24.1 17.1 8.3 2.8 -0.8 -1.4 0.4 0.7 -0.8 1.2 3.9 1.8
[19] 1.5
> Data$x3
[1] 1366 1519 1644 1893 2311 2998 4044 5046 5846 6420 6796 7159 7858 8622 9398
[16] 10542 12336 14040 16024
> str(Data)#查看数据的结构
'data.frame': 19 obs. of 5 variables:
$ year: int 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 ...
$ y : num 15.7 15 14.4 13 11.6 ...
$ x1 : int 15037 17001 18718 21826 26937 35260 48108 59811 70142 78061 ...
$ x2 : num 18.8 18 3.1 3.4 6.4 14.7 24.1 17.1 8.3 2.8 ...
$ x3 : int 1366 1519 1644 1893 2311 2998 4044 5046 5846 6420 ...
> summary(Data)#查看数据统计信息
year y x1 x2 x3
Min. :1988 Min. : 5.380 Min. : 15037 Min. :-1.400 Min. : 1366
1st Qu.:1992 1st Qu.: 6.700 1st Qu.: 31099 1st Qu.: 0.950 1st Qu.: 2654
Median :1997 Median :10.060 Median : 78061 Median : 3.100 Median : 6420
Mean :1997 Mean : 9.731 Mean : 83134 Mean : 6.484 Mean : 6624
3rd Qu.:2002 3rd Qu.:11.525 3rd Qu.:113582 3rd Qu.:11.500 3rd Qu.: 9010
Max. :2006 Max. :15.730 Max. :213132 Max. :24.100 Max. :16024
>
> lm1<-lm(y~x1+x2+x3,data = Data) #建立多元线性回归模型
> lm1 #打印参数估计的结果
Call:
lm(formula = y ~ x1 + x2 + x3, data = Data)
Coefficients:
(Intercept) x1 x2 x3
15.7197750 0.0003751 0.0497390 -0.0056601
>
也就是:y=0.0003751 * x1 + 0.0497390 * x2 + (-0.0056601) * x3 + 15.7197750
1.3 显著性检验
#显著性检验
> summary(lm1)
Call:
lm(formula = y ~ x1 + x2 + x3, data = Data)
Residuals:
Min 1Q Median 3Q Max
-1.4613 -0.6229 -0.0797 0.7153 1.2592
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.7197750 0.8702058 18.064 1.37e-11 ***
x1 0.0003751 0.0001061 3.535 0.00300 **
x2 0.0497390 0.0329629 1.509 0.15209
x3 -0.0056601 0.0014259 -3.969 0.00123 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9091 on 15 degrees of freedom
Multiple R-squared: 0.9363, Adjusted R-squared: 0.9236
F-statistic: 73.5 on 3 and 15 DF, p-value: 3.379e-09
>
其中
Estimate Std. Error t value Pr(>|t|)
估值,标准误差,T值,P值
P值小于0.05的变量,在统计意义上对因变量y的线性回归具有显著意义
所以,截距项(Intercept)和x1,x3通过显著性检验
Multiple R-squared和Adjusted R-squared这两个值,常称之为“拟合优度”和“修正的拟合优度”,是指回归方程对样本的拟合程度几何,这里我们可以看到,修正的拟合优度=0.9263,也就是大概拟合程度大概九成多一点,这个值当然是越高越好
F-statistic,也就是常说的F检验,常常用于判断方程整体的显著性检验,其P值为3.379e-09,显然是<0.05的,我们可以认为方程在P=0.05的水平上还是通过显著性检验的。
总结:
T检验是检验解释变量的显著性的;
R-squared是查看方程拟合程度的;
F检验是检验方程整体显著性的;
1.4 残差分析(我不是特别理解含义)
> par(mfrow=c(2,2))#一页多图,一页四图(不重叠)
> plot(lm1)
>
> #关于残差的分析图
> #残差和拟合值(左上)
> #残差QQ图(右上)
> #标准化残差平方根和拟合值(左下)
> #标准化残差和杠杆值(右下)
1.5 拿1988-2006的模型预测2020,发现与实际的2020的人口自然增长率不符(毕竟数据老了很多)
以2020年,人均GDP72447元,CPI上涨2.5%,国民总收入1009151亿元,人口自然增长率0.145% x1=1009151,x2=2.5,x3=72447
> newdata<-data.frame(year=2020,x1=1009151,x2=2.5,x3=72447)
> predict<-predict(lm1,newdata = newdata,interval = "predict")
> predict
fit lwr upr
1 -15.69411 -28.39739 -2.990832
所以用1988-2006年的模型预测2020年并不准确
2、下载UCI中wine数据集:http://archive.ics.uci.edu/ml/datasets/Wine。所下载数据可以用txt打开,其中每一行数据为一种Wine的记录,每条记录包含14个维度,其中第一维为该Wine类别,后面13维为具体的Wine属性。请基于所有的178个Wine样本对Wine的13个维度进行PCA降维分析,将贡献率之和大于90%的成分提取,并将原13维属性数据映射为新数据。
主成分分析直接调用函数就行,但是13个属性的累计贡献率之和怎么都在90%以上啊??!!!,后面怎么做?不晓得~
> wine<-read.table(file = "C:\\Users\\15328\\Desktop\\数据统计与分析基础\\wine.data",
+ header = FALSE,
+ sep=',')
> wine
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
1 1 14.23 1.71 2.43 15.6 127 2.80 3.06 0.28 2.29 5.64 1.040 3.92 1065
2 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.050 3.40 1050
3 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.68 1.030 3.17 1185
4 1 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.80 0.860 3.45 1480
5 1 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.32 1.040 2.93 735
6 1 14.20 1.76 2.45 15.2 112 3.27 3.39 0.34 1.97 6.75 1.050 2.85 1450
7 1 14.39 1.87 2.45 14.6 96 2.50 2.52 0.30 1.98 5.25 1.020 3.58 1290
8 1 14.06 2.15 2.61 17.6 121 2.60 2.51 0.31 1.25 5.05 1.060 3.58 1295
9 1 14.83 1.64 2.17 14.0 97 2.80 2.98 0.29 1.98 5.20 1.080 2.85 1045
10 1 13.86 1.35 2.27 16.0 98 2.98 3.15 0.22 1.85 7.22 1.010 3.55 1045
11 1 14.10 2.16 2.30 18.0 105 2.95 3.32 0.22 2.38 5.75 1.250 3.17 1510
12 1 14.12 1.48 2.32 16.8 95 2.20 2.43 0.26 1.57 5.00 1.170 2.82 1280
13 1 13.75 1.73 2.41 16.0 89 2.60 2.76 0.29 1.81 5.60 1.150 2.90 1320
14 1 14.75 1.73 2.39 11.4 91 3.10 3.69 0.43 2.81 5.40 1.250 2.73 1150
15 1 14.38 1.87 2.38 12.0 102 3.30 3.64 0.29 2.96 7.50 1.200 3.00 1547
16 1 13.63 1.81 2.70 17.2 112 2.85 2.91 0.30 1.46 7.30 1.280 2.88 1310
17 1 14.30 1.92 2.72 20.0 120 2.80 3.14 0.33 1.97 6.20 1.070 2.65 1280
18 1 13.83 1.57 2.62 20.0 115 2.95 3.40 0.40 1.72 6.60 1.130 2.57 1130
19 1 14.19 1.59 2.48 16.5 108 3.30 3.93 0.32 1.86 8.70 1.230 2.82 1680
20 1 13.64 3.10 2.56 15.2 116 2.70 3.03 0.17 1.66 5.10 0.960 3.36 845
21 1 14.06 1.63 2.28 16.0 126 3.00 3.17 0.24 2.10 5.65 1.090 3.71 780
22 1 12.93 3.80 2.65 18.6 102 2.41 2.41 0.25 1.98 4.50 1.030 3.52 770
23 1 13.71 1.86 2.36 16.6 101 2.61 2.88 0.27 1.69 3.80 1.110 4.00 1035
24 1 12.85 1.60 2.52 17.8 95 2.48 2.37 0.26 1.46 3.93 1.090 3.63 1015
25 1 13.50 1.81 2.61 20.0 96 2.53 2.61 0.28 1.66 3.52 1.120 3.82 845
26 1 13.05 2.05 3.22 25.0 124 2.63 2.68 0.47 1.92 3.58 1.130 3.20 830
27 1 13.39 1.77 2.62 16.1 93 2.85 2.94 0.34 1.45 4.80 0.920 3.22 1195
28 1 13.30 1.72 2.14 17.0 94 2.40 2.19 0.27 1.35 3.95 1.020 2.77 1285
29 1 13.87 1.90 2.80 19.4 107 2.95 2.97 0.37 1.76 4.50 1.250 3.40 915
30 1 14.02 1.68 2.21 16.0 96 2.65 2.33 0.26 1.98 4.70 1.040 3.59 1035
31 1 13.73 1.50 2.70 22.5 101 3.00 3.25 0.29 2.38 5.70 1.190 2.71 1285
32 1 13.58 1.66 2.36 19.1 106 2.86 3.19 0.22 1.95 6.90 1.090 2.88 1515
33 1 13.68 1.83 2.36 17.2 104 2.42 2.69 0.42 1.97 3.84 1.230 2.87 990
34 1 13.76 1.53 2.70 19.5 132 2.95 2.74 0.50 1.35 5.40 1.250 3.00 1235
35 1 13.51 1.80 2.65 19.0 110 2.35 2.53 0.29 1.54 4.20 1.100 2.87 1095
36 1 13.48 1.81 2.41 20.5 100 2.70 2.98 0.26 1.86 5.10 1.040 3.47 920
37 1 13.28 1.64 2.84 15.5 110 2.60 2.68 0.34 1.36 4.60 1.090 2.78 880
38 1 13.05 1.65 2.55 18.0 98 2.45 2.43 0.29 1.44 4.25 1.120 2.51 1105
39 1 13.07 1.50 2.10 15.5 98 2.40 2.64 0.28 1.37 3.70 1.180 2.69 1020
40 1 14.22 3.99 2.51 13.2 128 3.00 3.04 0.20 2.08 5.10 0.890 3.53 760
41 1 13.56 1.71 2.31 16.2 117 3.15 3.29 0.34 2.34 6.13 0.950 3.38 795
42 1 13.41 3.84 2.12 18.8 90 2.45 2.68 0.27 1.48 4.28 0.910 3.00 1035
43 1 13.88 1.89 2.59 15.0 101 3.25 3.56 0.17 1.70 5.43 0.880 3.56 1095
44 1 13.24 3.98 2.29 17.5 103 2.64 2.63 0.32 1.66 4.36 0.820 3.00 680
45 1 13.05 1.77 2.10 17.0 107 3.00 3.00 0.28 2.03 5.04 0.880 3.35 885
46 1 14.21 4.04 2.44 18.9 111 2.85 2.65 0.30 1.25 5.24 0.870 3.33 1080
47 1 14.38 3.59 2.28 16.0 102 3.25 3.17 0.27 2.19 4.90 1.040 3.44 1065
48 1 13.90 1.68 2.12 16.0 101 3.10 3.39 0.21 2.14 6.10 0.910 3.33 985
49 1 14.10 2.02 2.40 18.8 103 2.75 2.92 0.32 2.38 6.20 1.070 2.75 1060
50 1 13.94 1.73 2.27 17.4 108 2.88 3.54 0.32 2.08 8.90 1.120 3.10 1260
51 1 13.05 1.73 2.04 12.4 92 2.72 3.27 0.17 2.91 7.20 1.120 2.91 1150
52 1 13.83 1.65 2.60 17.2 94 2.45 2.99 0.22 2.29 5.60 1.240 3.37 1265
53 1 13.82 1.75 2.42 14.0 111 3.88 3.74 0.32 1.87 7.05 1.010 3.26 1190
54 1 13.77 1.90 2.68 17.1 115 3.00 2.79 0.39 1.68 6.30 1.130 2.93 1375
55 1 13.74 1.67 2.25 16.4 118 2.60 2.90 0.21 1.62 5.85 0.920 3.20 1060
56 1 13.56 1.73 2.46 20.5 116 2.96 2.78 0.20 2.45 6.25 0.980 3.03 1120
57 1 14.22 1.70 2.30 16.3 118 3.20 3.00 0.26 2.03 6.38 0.940 3.31 970
58 1 13.29 1.97 2.68 16.8 102 3.00 3.23 0.31 1.66 6.00 1.070 2.84 1270
59 1 13.72 1.43 2.50 16.7 108 3.40 3.67 0.19 2.04 6.80 0.890 2.87 1285
60 2 12.37 0.94 1.36 10.6 88 1.98 0.57 0.28 0.42 1.95 1.050 1.82 520
61 2 12.33 1.10 2.28 16.0 101 2.05 1.09 0.63 0.41 3.27 1.250 1.67 680
62 2 12.64 1.36 2.02 16.8 100 2.02 1.41 0.53 0.62 5.75 0.980 1.59 450
63 2 13.67 1.25 1.92 18.0 94 2.10 1.79 0.32 0.73 3.80 1.230 2.46 630
64 2 12.37 1.13 2.16 19.0 87 3.50 3.10 0.19 1.87 4.45 1.220 2.87 420
65 2 12.17 1.45 2.53 19.0 104 1.89 1.75 0.45 1.03 2.95 1.450 2.23 355
66 2 12.37 1.21 2.56 18.1 98 2.42 2.65 0.37 2.08 4.60 1.190 2.30 678
67 2 13.11 1.01 1.70 15.0 78 2.98 3.18 0.26 2.28 5.30 1.120 3.18 502
68 2 12.37 1.17 1.92 19.6 78 2.11 2.00 0.27 1.04 4.68 1.120 3.48 510
69 2 13.34 0.94 2.36 17.0 110 2.53 1.30 0.55 0.42 3.17 1.020 1.93 750
70 2 12.21 1.19 1.75 16.8 151 1.85 1.28 0.14 2.50 2.85 1.280 3.07 718
71 2 12.29 1.61 2.21 20.4 103 1.10 1.02 0.37 1.46 3.05 0.906 1.82 870
[ reached 'max' / getOption("max.print") -- omitted 107 rows ]
#到达最大显示幅度可能?后面还有107行没有显示出来
> pc_wine<-princomp(wine[,2:14])#主成分分析
> pc_wine
Call:
princomp(x = wine[, 2:14])
Standard deviations:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9 Comp.10 Comp.11
314.07718175 13.09831925 3.06350952 2.22781020 1.10541467 0.91451560 0.52669370 0.38798300 0.33386675 0.26702019 0.19329997
Comp.12 Comp.13
0.14475490 0.09031952
13 variables and 178 observations.
> summary(pc_wine)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9
Standard deviation 314.0771817 13.098319252 3.063510e+00 2.227810e+00 1.105415e+00 9.145156e-01 5.266937e-01 3.879830e-01 3.338668e-01
Proportion of Variance 0.9980912 0.001735916 9.495896e-05 5.021736e-05 1.236368e-05 8.462130e-06 2.806815e-06 1.523081e-06 1.127830e-06
Cumulative Proportion 0.9980912 0.999827146 9.999221e-01 9.999723e-01 9.999847e-01 9.999931e-01 9.999960e-01 9.999975e-01 9.999986e-01
Comp.10 Comp.11 Comp.12 Comp.13
Standard deviation 2.670202e-01 1.933000e-01 1.447549e-01 9.031952e-02
Proportion of Variance 7.214158e-07 3.780603e-07 2.120138e-07 8.253928e-08
Cumulative Proportion 9.999993e-01 9.999997e-01 9.999999e-01 1.000000e+00
>
# 第一行是特征值(Standard deviation),
# 第二列是方差的贡献率(Proportion of Variance)
# 第三列是累计方差的贡献率(Cumulative Proportion)
# 方差的贡献率: 标准化后的特征值,全部相加等于100%
# 累计方差的贡献率:累加后的方差的贡献率
3、聚类分析
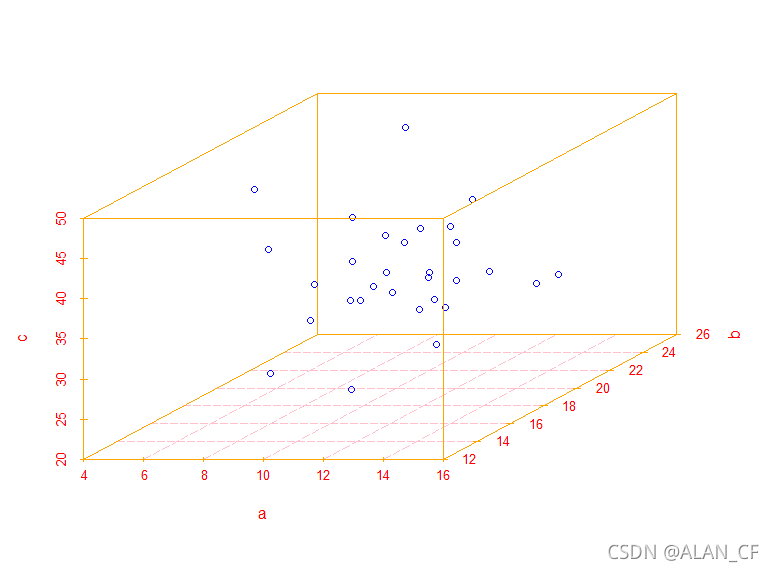
(1)随机生成均值、方差各不相同,且相互之间有少量交叉的3个类,每类30个样本,用不同的颜色进行展示。
> a<-rnorm(30,10,2)#样本数量、均值、标准差各不相同
> b<-rnorm(30,20,4)
> c<-rnorm(30,36,6)
> summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
5.587 8.955 9.632 9.933 11.151 14.399
> summary(b)
Min. 1st Qu. Median Mean 3rd Qu. Max.
13.70 18.35 19.95 20.24 21.37 25.62
> summary(c)
Min. 1st Qu. Median Mean 3rd Qu. Max.
22.18 31.42 32.86 34.17 38.34 46.35
> a
[1] 9.524986 9.280957 8.856085 11.429310 9.251991 8.627237 7.606568 12.151841 9.624943 11.719732 12.687304 12.134777 10.047509 14.398540
[15] 9.263212 7.219364 7.759353 10.816147 9.638876 10.216056 10.823944 10.573994 8.824954 7.509732 11.260270 5.587230 12.243530 9.953913
[29] 9.571754 9.396327
> b
[1] 18.19843 13.70380 25.61854 19.68710 19.17396 19.78770 19.12725 16.60318 17.91749 20.45248 24.86621 19.38487 24.46448 20.43895 18.56120 25.48773
[17] 25.35885 18.28004 22.03702 18.20893 20.86706 20.84360 17.18387 16.79552 20.61161 19.41235 21.53978 22.01808 20.11724 20.39201
> c
[1] 37.78435 28.83921 31.84021 31.30081 31.77410 41.40340 29.40073 41.94260 22.17640 32.84960 28.70440 40.78994 38.55480 32.53705 32.52373 46.35303
[17] 23.82788 33.76297 37.59299 34.60493 24.47531 32.87408 35.99738 40.80707 29.31982 45.31903 32.78607 32.17224 34.23691 38.52554
>
> scatterplot3d(x=a,y=b,z=c,color="blue",
col.grid = "pink",col.lab = "red",
col.axis = "orange",lty.grid = 5) #绘制三维散点图
> > data4_3<-1:30 #给一个向量,标注1到30的顺序
> data4_3
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
[29] 29 30
> data4_3_a<-data.frame(data4_3,a) #建立 数据框
> data4_3_a
data4_3 a
1 1 9.524986
2 2 9.280957
3 3 8.856085
4 4 11.429310
5 5 9.251991
6 6 8.627237
7 7 7.606568
8 8 12.151841
9 9 9.624943
10 10 11.719732
11 11 12.687304
12 12 12.134777
13 13 10.047509
14 14 14.398540
15 15 9.263212
16 16 7.219364
17 17 7.759353
18 18 10.816147
19 19 9.638876
20 20 10.216056
21 21 10.823944
22 22 10.573994
23 23 8.824954
24 24 7.509732
25 25 11.260270
26 26 5.587230
27 27 12.243530
28 28 9.953913
29 29 9.571754
30 30 9.396327
> data4_3_b<-data.frame(data4_3,b)
> data4_3_b
data4_3 b
1 1 18.19843
2 2 13.70380
3 3 25.61854
4 4 19.68710
5 5 19.17396
6 6 19.78770
7 7 19.12725
8 8 16.60318
9 9 17.91749
10 10 20.45248
11 11 24.86621
12 12 19.38487
13 13 24.46448
14 14 20.43895
15 15 18.56120
16 16 25.48773
17 17 25.35885
18 18 18.28004
19 19 22.03702
20 20 18.20893
21 21 20.86706
22 22 20.84360
23 23 17.18387
24 24 16.79552
25 25 20.61161
26 26 19.41235
27 27 21.53978
28 28 22.01808
29 29 20.11724
30 30 20.39201
> data4_3_c<-data.frame(data4_3,c)
> data4_3_c
data4_3 c
1 1 37.78435
2 2 28.83921
3 3 31.84021
4 4 31.30081
5 5 31.77410
6 6 41.40340
7 7 29.40073
8 8 41.94260
9 9 22.17640
10 10 32.84960
11 11 28.70440
12 12 40.78994
13 13 38.55480
14 14 32.53705
15 15 32.52373
16 16 46.35303
17 17 23.82788
18 18 33.76297
19 19 37.59299
20 20 34.60493
21 21 24.47531
22 22 32.87408
23 23 35.99738
24 24 40.80707
25 25 29.31982
26 26 45.31903
27 27 32.78607
28 28 32.17224
29 29 34.23691
30 30 38.52554
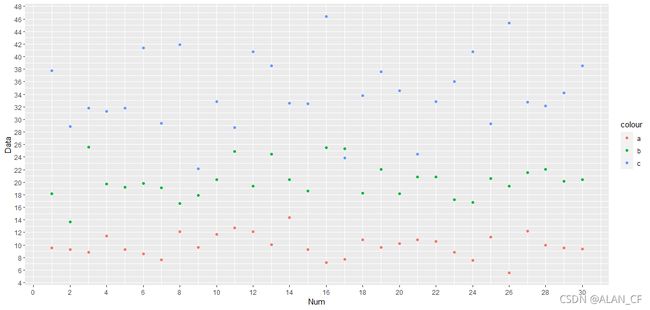
> library(ggplot2)
> ggplot()+
+ geom_point(data = data4_3_a, aes(x=data4_3,y=a,color = "a"))+
+ geom_point(data = data4_3_b, aes(x=data4_3,y=b,color = "b"))+
+ geom_point(data = data4_3_c, aes(x=data4_3,y=c,color = "c"))+
+ scale_x_continuous(breaks = seq(0,30,by=2))+
+ scale_y_continuous(breaks = seq(0,48,by=2))+
+ labs(x="Num",y="Data") #绘图,三类数据,二维平面图
>
>
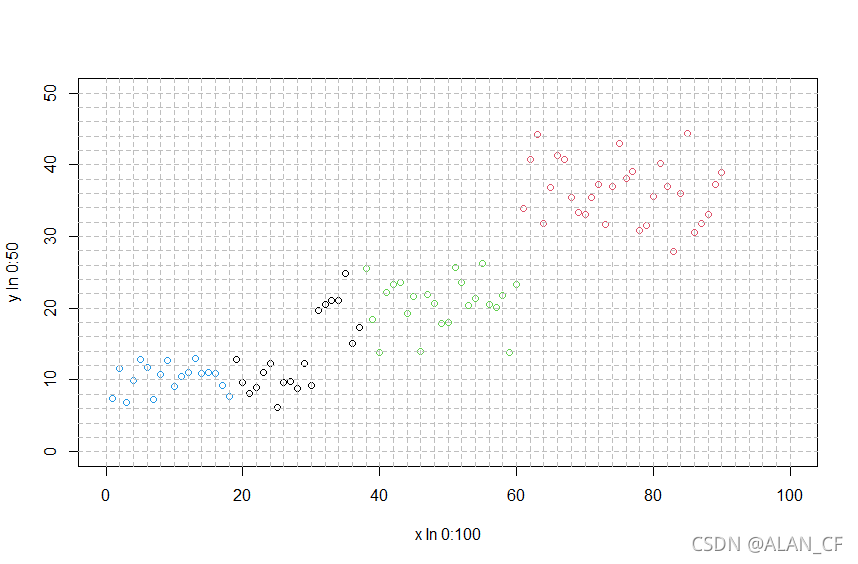
(2)通过keamns聚类分析,将所有的数据分成3类、4类、5类,每一类用不同颜色展示。
> for(i in 1:90){
+ if(i <= 30)
+ {
data_new[i]=a[i]}
+ if(i <= 60 && i > 30)
+ {
data_new[i]=b[i-30]}
+ if(i <= 90 && i > 60)
+ {
data_new[i]=c[i-60]}
+ }
> data_new
[1] 7.456319 11.572397 6.814606 9.938019 12.815763
[6] 11.686153 7.262254 10.710768 12.698461 9.074380
[11] 10.551535 11.024495 13.008572 10.851654 11.024795
[16] 10.864380 9.171385 7.704503 12.859385 9.675335
[21] 8.070182 8.990059 11.060694 12.257815 6.172478
[26] 9.682554 9.763029 8.748758 12.251217 9.172198
[31] 19.738764 20.501748 21.054288 21.150245 24.835484
[36] 15.102064 17.256718 25.605664 18.385802 13.866511
[41] 22.200251 23.379533 23.595921 19.323490 21.577638
[46] 13.972503 21.969029 20.642763 17.897801 18.033550
[51] 25.691461 23.625472 20.413657 21.351698 26.189629
[56] 20.544046 20.083766 21.843806 13.827343 23.360183
[61] 33.939320 40.796937 44.281133 31.876346 36.784914
[66] 41.273806 40.731411 35.386068 33.342416 33.030830
[71] 35.485651 37.214781 31.690202 37.027441 43.003857
[76] 38.083299 39.001923 30.823535 31.524934 35.586099
[81] 40.173552 36.926101 27.854280 35.954891 44.401148
[86] 30.583698 31.839231 33.006067 37.236035 38.956257
> x_zhou<-1:90
> data_newx<-data.frame(x_zhou,data_new)
> #3
> result3<-kmeans(data_newx,3)
> plot(data_newx,col=result3$cluster,xlab="x In 0:100",ylab="y In 0:50",,xlim=c(0,100),ylim=c(0,50))
> abline(v=seq(0,100,by=2),h=seq(0,50,by=2),lty=2,col="grey")
> #4
> result4<-kmeans(data_newx,4)
> plot(data_newx,col=result4$cluster,xlab="x In 0:100",ylab="y In 0:50",,xlim=c(0,100),ylim=c(0,50))
> abline(v=seq(0,100,by=2),h=seq(0,50,by=2),lty=2,col="grey")
> #5
> result5<-kmeans(data_newx,centers = 5)
> plot(data_newx,col=result5$cluster,xlab="x In 0:100",ylab="y In 0:50",,xlim=c(0,100),ylim=c(0,50))
> abline(v=seq(0,100,by=2),h=seq(0,50,by=2),lty=2,col="grey")
>
4、随机生成完全不交叉的2个类,每个类包含30个样本,用SVM进行分类和返回所有支撑向量,并以合适方式进行Figure展示。