《深度卷积神经网络原理与实践》笔记 第一章 机器学习基础
本笔记是依据周浦城等教授编著的《深度卷积神经网络原理与实践》的个人笔记(Version:1.0.2)
整理作者:sq_csl
第一章 机器学习基础
1.1 机器学习概述
1.1.1 概念
概念
ML(Machine Learning)是一门发展了比较长时间的学科,其在发展过程中定义也发生了一些变化
早期概念源于Tom Mitchell:假设用 P P P来评估计算机程序在某个任务类 T T T上的性能,若某程序利用经验 E E E在任务类 T T T上获得了性能改善,那么认为关于 T T T和 P P P,这个程序对 E E E进行了学习。
但随着研究深入,内涵和外延也在发生变化,目前大家的普遍认知:ML专门研究计算机如何模拟、实现人的学习行为用来获得新的知识、技能,重新组织已有的知识结构使得其不断改善系统自身的性能。
目的
机器学习的目的:学习到的模型能够很好的适用于新样本,而不仅仅是训练集本身(所以也需要测试集)。
1.1.2 机器学习的任务
分类
D a t a ⇒ Data⇒ Data⇒ f : R d ➡ Z f:R^d➡Z f:Rd➡Z,它是一种从向量到整数的映射。
其中 R d R^d Rd为样本集, Z Z Z为标签集。
如果标签数量为2,那么是二分类问题,一般类别标签设置为 + 1 、 − 1 +1、-1 +1、−1,如果涉及到多个类别,则为多分类问题
举例:身高1.75m,体重100kg的男人肥胖吗? 根据肿瘤的体积、患者的年龄来判断肿瘤的良性或恶性?
回归
D a t a ⇒ Data⇒ Data⇒ f : R d ➡ R f:R^d➡R f:Rd➡R,它是一种从自变量到因变量的映射。
其中 R d R^d Rd为自变量集, R R R为因变量集。
根据函数表达式的不同,可将回归分为线性回归和非线性回归。也可根据因变量和自变量的数量不同,将回归分为一元回归和多元回归。
举例:如何预测曹县的房价?未来一个月的某板块股票的走向?
排序
使用机器学习方法,得到数据特征排序的模型,通过模型来得到排序结果。
根据训练数据的不同,排序学习方法可分为:pointwise(基于单个样本)、pairwise(基于样本对)、listwise(基于样本列表)
聚类
聚类算法将样本集根据样本之间的相似性,将样本之间划分成多个不相交的簇。
常见的聚类算法:
划分聚类:K-Means、K-Medoids等
层次聚类:BIRCH、ROCK等
密度聚类:DBSCAN(可参考周志华教授《机器学习》)、OPTICS、DENCLUE等
网络聚类:STING、CLIQUE、waveCluster等
模型聚类分基于概率模型聚类和基于神经网络模型聚类两种,主要有:GMM、基于PagerRank的聚类、SOM
举例:如何将教室里的学生按性格、爱好划分为5类?
降维
通过某种数学变换将原始的高维度属性空间的样本映射到低维度的子空间,并保证其中所包含的有效信息不会丢失,这是一种预处理的重要手段。
降维算法可以根据策略的不同进行不同的分类:
根据样本信息是否可利用:监督降维、半监督降维、无监督降维
处理的类型:线性降维(PCA、ICA、LDA等)、非线性降维(Isomap、LLE、kernel PCA等)
1.1.3 机器学习的发展简史
机器学习的发展大致可以分为以下五个阶段:(以下不讲历史,列出一些此时期出现的方法)
奠基时期
Adaline模型和学习方法
瓶颈时期
感知机
重振时期
反向传播(BP)
决策树:ID3、C4.5、CART
成型时期
Boosting:AdaBoost算法等
支持向量机(SVM)
随机森林(RF)
在此时期,研究发现,在应用反向传播(BP)算法进行神经网络的训练时,易出现由于神经元饱和而导致的梯度消失的现象。
爆发时期
通过无监督学习方法逐层训练算法,再使用有监督的BP算法进行调优解决深度神经网络在训练上的问题。
DL(Deep Learning)发展
1.2 机器学习策略
有监督学习(SL)
常见:决策树、k邻接算法(kNN)、朴素贝叶斯分类器(NBC)等
无监督学习(UL)
常见:稀疏自编码(SAE)、主成分分析(PCA)、K-Means、最大期望(EM)
半监督学习(SSL)
可分为:半监督分类、半监督回归、半监督聚类和半监督降维
常见的半监督学习有直推式和归纳式两种模式。
强化学习(RL)
将DL应用于RL,可形成深度强化学习。
1.3 模型评估与选择
1.3.1 归纳偏好
丑小鸭定理:不存在与问题无关的“优越”的或“最好”的特征集合或属性集合。
没有免费的午餐:所有搜索代价函数极值的算法在平均到所有可能的代价函数上时,其表现都恰好是相同的;特别地,如果算法A在一些代价函数上优于算法B,那么一定存在其它一些函数,使得B优于A。
最小描述长度(MDL):必须使模型的算法复杂度及与该模型相适应的训练数据的描述长度的和最小。(体现了“奥卡姆剃刀”原理)
1.3.2 数据集划分
误差:预测输出与真实输出之间的差异
训练误差、经验误差:算法模型在训练集上的差异
泛化误差:算法模型在新样本上的误差
通常将数据集 D D D拆分成训练集 S S S和测试集 T T T。假设 T T T是从样本真实分布中独立采样得到的,就可以将 T T T上的误差近似为泛化误差,从而同时根据训练误差和测试误差对学习算法进行性能评估。
要充分利用已有的有限数量的数据集来构造一个规模尽量大的数据集,主要的技术包括留出法、自助法、交叉验证法等
1.3.3 性能度量
性能度量不仅取决于算法和数据,还应该反映具体的任务需求。
错误率和精度
错误率(error rate):错分样本的数量占样本总量的比例

精度(accuracy):分对的样本的数量占样本总数的比例

这里的 I I ( . ) II(.) II(.)是指示函数,若 . . .为真则取1,否则取值为0。
查准率、查全率和F1度量
查准率P(Precision)与查全率R(Recall)分别定义为:
![]()
![]()
其中:
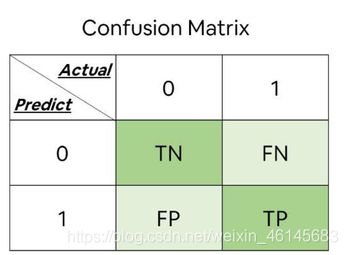
TP:真正例(true positive),即真实结果和预测结果都是正例。
FP:假正例(false positive),即真实结果是反例,预测结果是正例。
TN:真反例(true negative),即真实结果和预测结果都是反例。
FN:假反例(false negative),即真实结果是正例,预测结果是反例。
因此,学习模型对测试数据集输出一系列为正样本的概率,根据概率由大到小排列,然后依次设置阈值,若大于该阈值,则为正样本;反之则为负样本。每次阈值的设置都有对应的查准率和查全率,因此以查全率为横坐标,查准率为纵坐标,就可以得到查准率-查全率曲线,也称作”P-R"曲线。
1.3.4 过拟合、欠拟合
如果模型没有很好的捕捉到数据特征,对训练样本的一般性质尚未学习好,不能很好拟合数据,导致得到的模型在训练集上的表现差,就被称为欠拟合。(可能原因:模型本身过于简单;特征数量太少)
如果在训练集上表现好,但在测试集上表现差(可能原因:模型本身过于复杂;训练样本缺乏代表性)
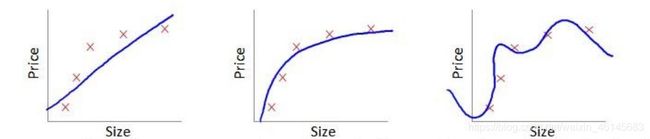
(从左到右分别为:欠拟合、好的拟合、过拟合)
1.4 神经网络与深度学习
1.4.1 生物神经元(略)
1.4.2 人工神经网络
M-P模型

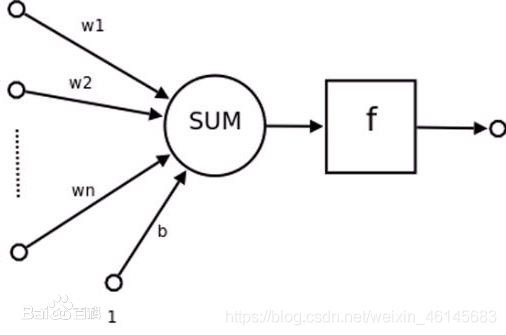
其中, x 1 x_1 x1, x 2 x_2 x2,…, x n x_n xn为神经元P的n个输入节点; w 1 w_1 w1, w 2 w_2 w2,…, w n w_n wn为权值, θ θ θ是神经元阈值; y y y是神经元的输出,那么输出函数为下式:
y = f ( ( ∑ i = 1 n w i x i ) + θ y=f(\displaystyle \left( \sum_{i=1}^n w_i x_i \right)+θ y=f((i=1∑nwixi)+θ
其中, f f f为激活函数。激活函数的不同,神经元模型也不同。
感知机
假设输入特征向量空间为 x ∈ R n x∈R^n x∈Rn,输出的类标签空间为 y = y= y={ − 1 , + 1 -1,+1 −1,+1}, f f f为符号函数(有文献记作 s g n sgn sgn函数), W = ( w 1 , w 2 , . . . , w n ) T W=(w1,w2,...,wn)^T W=(w1,w2,...,wn)T, x x x和 b b b分别为神经元的神经向量和偏置(bias),则模型为:
y = f ( W T x + b ) y=f(W^Tx+b) y=f(WTx+b)
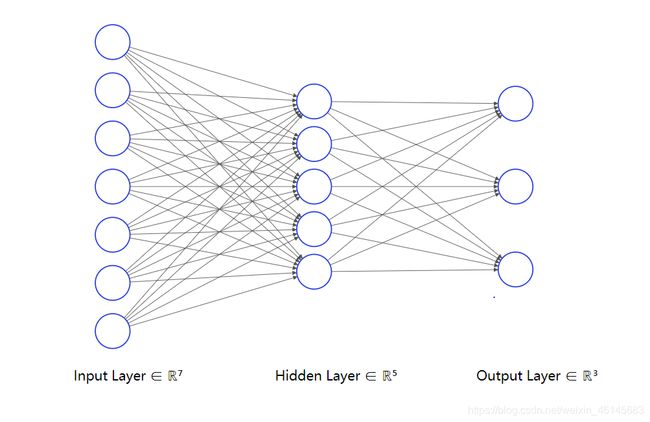
多层感知机
在输入层和输出层之间加上隐藏层(Hidden Layer),就构成了多层感知机。
1.4.3 深度学习
产生背景
为了解决传统机器学习中人工设计特征的不足,采用类似大脑皮层的分层结构,不仅极大的降低了视觉系统处理的数据量,而且显著提升了鲁棒性和认知效率。
深度学习的提出(略)
与浅层学习的区别
模型结构方面:学得的模型中非线性操作的层级数变得更多
特征学习方面:对原始信号逐层进行特征变换,得到层次化的特征表示,可更好的刻画数据的内在信息
避免了繁杂的特征提取,更好的实现了复杂的函数逼近。
深度学习模型
DAE
CNN
RNN
(第一章 完结)