相机标定与3D重建(opencv-python实现)

1. 相机标定的四个坐标系以及转换关系

1.1 四个坐标系介绍

1.1.1 世界坐标系(X_w, Y_w, Z_w)

1. 为了描述相机位置而被引入的
2. 标定时确定标定物的位置
3. 作为双目视觉的系统参考系，给出两个摄像机对世界坐标系的关系，从而求出相机之间的相对关系
4. 作为重建得到三维坐标的容器，重放重建后的物体的三维坐标

1.1.2 摄像机坐标系(X_c, Y_c, Z_c)

摄像机坐标系是摄像机站在自己角度上衡量的物体的坐标系。摄像机坐标系的原点在摄像机的光心上，z轴与摄像机光轴平行。

1.1.3 图像坐标系(x,y)

主要用于表征从摄像机坐标系向图像坐标系的透视投影关系，特点为连续，原点位于摄像机光轴与成像平面的焦点上

1.1.4 像素坐标系(u,v)

我们能从摄像机得到的真实信息，特点为离散，原点位于图像的左上角，其实是存储器的首地址

1.2 简单知识介绍

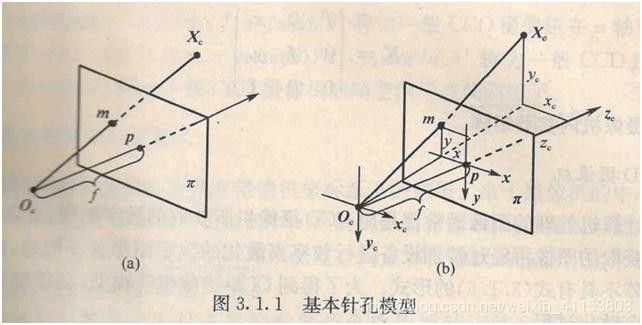
上图是针孔摄像机的基本模型。平面π称为摄像机的像平面，点O_c称为摄像机中心（或光心），f成为摄像机的焦距，O_c为端点且垂直于像平面的射线成为光轴或主轴，主轴与像平面的交点p是摄像机的主点

1.3 图像坐标系与像素坐标系的关系

如上图所示，像素坐标系u-v的原点为O₀，图像坐标系x-y的原点O₁在像素坐标系u-v的坐标为（u₀，v₀），dx和dy分别表示每个像素在横轴x和纵轴y的物理尺寸则图像坐标系和像素坐标系的坐标关系如下所示：
$$u=\frac{x}{dx}+u_0$$$$v=\frac{x}{dx}+v_0$$
写成矩阵形式：
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{dx}& 0& u_0\\ 0& \frac{1}{dy}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

1.4 世界坐标系与摄像机坐标系的关系

世界坐标系的坐标可以通过刚体变换（旋转以及平移转换）为摄像机坐标系的坐标，如下图所示

可表现为如下：
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{ccc}{r}_{00}& r_{01}& r_{02}\\ r_{10}& r_{11}& r_{12}\\ r_{20}& r_{21}& r_{22}\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]+\left[\begin{array}{c}{T}_x\\ T_y\\ T_z\end{array}\right]$$
我们将旋转矩阵R以及平移矩阵T称之为摄像机的外参数
R可以表示为分别绕X,Y,Z轴旋转的效果之和，R=r1r2r3如下图所示：

1.5 摄像机坐标系、图像坐标系和像素坐标系三者之间的关系

摄像机坐标系中的坐标通过透视投影（用中心投影法将形体投射到投影面上）变为图像坐标系中的坐标

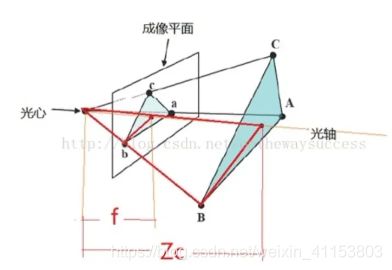
由简单的相似三角形可以得到
$$x=\frac{f}{Z_c}{X}_c$$$$y=\frac{f}{Z_c}{Y}_c$$
写成矩阵的形式为：
$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\frac{1}{Z_c}\left[\begin{array}{ccc}f& 0& 0\\ 0& f& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$
再由像素坐标系和图像坐标系的关系可得，中间矩阵也称为摄像机的内参矩阵：
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{Z_c}\left[\begin{array}{ccc}\frac{f}{dx}& 0& u_0\\ 0& \frac{f}{dy}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$

1.6 总结

世界坐标通过刚体变换(旋转和平移)得到摄像机坐标，摄像机坐标系通过透视投影转换为图像坐标，图像坐标离散化可得像素坐标
将以上步骤整理得：
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{Z_c}\left[\begin{array}{ccc}{f}_x& 0& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cc}R& t\\ 1& 0\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]$$
其中$$f_x=\frac{f}{dx},f_y=\frac{f}{dy}$$
1.第一个矩阵中的四个参数称之为相机的内部参数，因为他们只与相机有关
2.第二个矩阵的两个参数称之为相机的外部参数，只要世界坐标系的相对位置关系发生改变，它们就会改变，每一张图片的R、T都是唯一的
3.单目摄像机标定就是在已知像素坐标系下的坐标和世界坐标系下的坐标求解内部参数的过程
可以简化为：
$$s\ast m=A\left[\begin{array}{cc}R& t\end{array}\right]M$$
其中s就是Z_c，称之为尺度因子,m为图像坐标系的坐标，A为内参矩阵，M为世界坐标系中的坐标

为了能够更好的理解相机内参，举个实例：
现以NiKon D700相机为例进行求解其内参数矩阵：
就算大家身边没有这款相机也无所谓，可以在网上百度一下，很方便的就知道其一些参数——
焦距 f = 35mm 最高分辨率：4256×2832 传感器尺寸：36.0×23.9 mm
根据以上定义可以有：
u₀= 4256/2 = 2128 v₀= 2832/2 = 1416 dx = 36.0/4256 dy = 23.9/2832
f_x = f/dx = 4137.8 f_y = f/dy = 4147.3
分辨率可以分为显示分辨率与图像分辨率两个方向：
显示分辨率（屏幕分辨率）是屏幕图像的精密度，是指显示器所能显示的像素有多少
图像分辨率则是单位英寸中所包含的像素点数，其定义更趋近于分辨率本身的定义

2 畸变模型

2.1 产生原因

采用理想针孔模型，由于通过针孔的光线少，摄像机曝光太慢，在实际使用中均采用透镜，可以使图像生成迅速，但代价是引入了畸变。两种主要的失真是径向失真和切向失真，而在张氏标定中，只关注径向畸变。

2.2 径向畸变

产生原因是光线在远离透镜中心的地方比靠近中心的地方更加弯曲，主要包括桶形畸变和枕形畸变：

其在真实照片中是这样的：

它可以被如下方法校正：
$$x_{corrected}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$$$y_{corrected}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$
其中k₁,k₂表示径向畸变的系数，r表示图像坐标到原点的距离

2.3 切向畸变

产生的原因透镜不完全平行于图像平面，这种现象发生于成像仪被粘贴在摄像机的时候：

$$x_{corrected}=x+[2p_{1}xy+p_2(r^2+2y^2)]$$$$y_{corrected}=y+[2p_{2}xy+p_1(r^2+2y^2)]$$

3 张正友标定算法详解

3.1 相机标定的目的

1. 进行摄像机标定的目的：求出相机的内、外参数，以及畸变参数
2. 标定相机后通常是想做两件事：一是由于每个镜头的畸变程度各不相同，通过相机标定可以矫正这种镜头畸变；另一个就是根据获得的图像重构三维场景

3.2 计算单应性矩阵

设三维世界坐标的点为X=[X,Y,Z,1]T，二维相机平面像素坐标为m=[u,v,1]T，所以标定用的棋盘格平面到图像平面的单应性关系为：
$$s\ast m=A\left[\begin{array}{cc}R& t\end{array}\right]M$$
其中s为尺度因子，A为摄像机内参数，R为旋转矩阵，T为平移向量。其中
$$A=\left[\begin{array}{ccc}{f}_x& c& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]$$
c是描述两个特征坐标轴倾斜角倾斜角的参数（两个坐标轴相互垂直时，c = 0,则默认情况下这个c都是为0）。

张氏标定法中，假设模型平面在世界坐标系中Z坐标为0，也就是我们把世界坐标系的原点定在物体上。则可得
$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K\left[\begin{array}{cccc}{r}_1& r_2& r_3& t\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 0\\ 1\end{array}\right]=K\left[\begin{array}{ccc}{r}_1& r_2& t\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]$$
我们把K[r₁ r₂ t]叫做单应性矩阵H，被定义为一个平面到另一个平面的投影映射
$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=H\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]$$$$H=\left[\begin{array}{ccc}{h}_1& h_2& h_3\end{array}\right]=\lambda K\left[\begin{array}{ccc}{r}_1& r_2& t\end{array}\right]$$
H是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H。

3.3 计算内参数矩阵

由上式可得
$$\lambda =\frac{1}{s}$$$$r_1=\frac{1}{\lambda }{K}^{-1}{h}_1$$$$r_2=\frac{1}{\lambda }{K}^{-1}{h}_2$$
由于旋转矩阵是个酉矩阵，r1和r2正交，可得
$$r_1^T{r}_2=0$$$$\Vert r_1\Vert =\Vert r_2\Vert =0$$
代入可得：
$$h_1^T{K}^{-T}{K}^{-1}{h}_2=0$$$$h_1^T{K}^{-T}{K}^{-1}{h}_1=h_2^T{K}^{-T}{K}^{-1}{h}_2$$
即每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。为了方便计算，定义如下：

可以看到，B是一个对称阵，所以B的有效元素为六个，让这六个元素写成向量b，即

可以推导得到

利用约束条件可以得到：

通过上式，我们至少需要三幅包含棋盘格的图像，可以计算得到B，然后通过cholesky分解，得到相机的内参数矩阵K。

3.3 计算外参数矩阵

$$\lambda =\frac{1}{s}=\frac{1}{\Vert A^{-1}{h}_1\Vert }=\frac{1}{\Vert A^{-1}{h}_2\Vert }$$$$r_1=\frac{1}{\lambda }{K}^{-1}{h}_1$$$$r_2=\frac{1}{\lambda }{K}^{-1}{h}_2$$$$r_3=r_1\times r_2$$$$t=\lambda K^{-1}{h}_3$$

3.4 最大似然估计

张正友在论文中提到，前面的这些数学原理和推导并没有太多的物理意义，仅仅是为后面的极大似然优化提供了一个初值。
极大似然估计是一种估计总体未知参数的方法，它主要用于点估计问题。说穿了就是一句话：就是在参数空间中选取使得样本取得观测值的概率最大的参数。
假设我们得到了模型平面的n幅图片，模型平面上有m个点，假设图像上像素点的噪声服从独立的同一分布，下面给出极大似然优化问题：$$\sum \sum \Vert m_{ij}-\hat{m}(A,R_i,t_i,M_j)\Vert$$
其中$$\hat{m}(A,R_i,t_i,M_j)$$表示Mj在第i副图像上的投影

4 张正友相机标定python实现

在张正友相机标定中，一般分为以下的步骤：

1. 准备一系列来相机标定的图片
2. 对每张图片提取角点信息
3. 由于角点信息不够精确，进一步提取亚像素角点信息
4. 在图片中画出提取出的角点
5. 相机标定
6. 对标定结果评价，计算误差
7. 使用标定结果对原图片进行校正

4.1 准备好一系列相机标定

在本次实验中我们选取的是opencv官方在github上提供的图片`

opencv/samples/data/left01-left14.jpg

4.2 对每张图片提取角点信息

# 导入图像
a = cv2.imread('E:/3Dreconstruction/camera calibration/chess/left14.jpg')
# 进行颜色空间的转换
b = cv2.cvtColor(a, cv2.COLOR_BGR2GRAY)
# 提取角点信息，表示每行角点的个数为9，每列角点的个数为6
ret, corners = cv2.findChessboardCorners(b, (9, 6))
# ret为标志位，用来检测是否检测到所有棋盘内角点
print(ret)

4.3 提取亚像素角点信息

# 迭代的终止标准
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 提取亚像素角点信息
corners2 = cv2.cornerSubPix(b, corners, (11, 11), (-1, -1), criteria)

4.4 画出角点

# 画出角点
cv2.drawChessboardCorners(a, (9, 6), corners2 ,False)
cv2.namedWindow('winname', cv2.WINDOW_NORMAL)
cv2.imshow('winname', a)
cv2.waitKey(0)

得如下图像：

4.5 相机标定

# 相机标定的核心
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(op, imgpoints, b.shape[::-1], None, None)
# ret为极大似然函数的最小值
# mtx是内参矩阵
# dist为相机的畸变参数矩阵
# rvecs为旋转向量
# tvecs为位移向量

4.6 标定结果评价，计算误差

tot_error = 0
for i in range(len(op)):
    imgpoints2, _ = cv2.projectPoints(op[i], rvecs[i], tvecs[i], mtx, dist) #对空间中的三维坐标点进行反向投影
    error = cv2.norm(imgpoints[i], imgpoints2, cv2.NORM_L2) / len(imgpoints2)   # 平均平方误差（重投影误差）
    tot_error += error
 print(ret, (tot_error / len(op))**0.5)

4.7 对原图像进行校正

h, w = a.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (h, w), 1) # 校正内参矩阵
dst = cv2.undistort(a, mtx, dist, None)
# undistort
mapx, mapy = cv2.initUndistortRectifyMap(mtx, dist, None, newcameramtx, (w, h), 5)  # 用于计算畸变映射
dst = cv2.remap(a, mapx, mapy, cv2.INTER_LINEAR)    # 把求得的映射应用到图像上
np.savez("outfile", mtx, dist)
a = cv2.cvtColor(a, cv2.COLOR_BGR2RGB)
dst = cv2.cvtColor(dst, cv2.COLOR_BGR2RGB)
plt.subplot(121), plt.imshow(a), plt.title('source')
plt.subplot(122), plt.imshow(dst), plt.title('undistorted')
plt.show()

得到校正结果
![在这里插入图片描述](https://img-blog.csdnimg.cn/20190622145959192.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MTE1MzgwMw==,size_16,color_FFFFFF,t_70

4.8 最终代码

import numpy as np
import cv2
from matplotlib import pyplot as plt
import time
import os

 # 程序流程
 # 1.准备好一系列来相机标定的图片
 # 2.对每张图片提取角点信息
 # 3.由于角点信息不够精确，进一步提取亚像素角点信息
 # 4.在图片中画出提取出的角点
 # 5.相机标定
 # 6.对标定结果评价，计算误差
 # 7.使用标定结果对原图片进行校正

path = 'E:/3Dreconstruction/camera calibration/chess2'   # 文件路径
objp = np.zeros((9 * 6, 3), np.float32)
objp[:, :2] = np.mgrid[0:9, 0:6].T.reshape(-1, 2) * 10
# mgrid是meshgrid的缩写，生成的是坐标网格，输出的参数是坐标范围，得到的网格的点坐标
op = [] # 存储世界坐标系的坐标X，Y，Z，在张正友相机标定中Z=0
imgpoints = []  # 像素坐标系中角点的坐标
for i in os.listdir(path):
    #读取每一张图片
    file = '/'.join((path, i))
    a = cv2.imread(file)
    b = cv2.cvtColor(a, cv2.COLOR_BGR2GRAY)
    # 确定输入图像中是否有棋盘格图案，并检测棋盘格的内角点
    ret, corners = cv2.findChessboardCorners(a, (9, 6), None)
    criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
    if ret == True: # 如果所有的内角点都找到了
        corners2 = cv2.cornerSubPix(b, corners, (11, 11), (-1, -1), criteria)   # 提取亚像素角点信息
        imgpoints.append(corners2)
        op.append(objp)

# 相机标定的核心
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(op, imgpoints, b.shape[::-1], None, None)
# ret为极大似然函数的最小值
# mtx是内参矩阵
# dist为相机的畸变参数矩阵
# rvecs为旋转向量
# tvecs为位移向量
tot_error = 0
for i in range(len(op)):
    imgpoints2, _ = cv2.projectPoints(op[i], rvecs[i], tvecs[i], mtx, dist) #对空间中的三维坐标点进行反向投影
    error = cv2.norm(imgpoints[i], imgpoints2, cv2.NORM_L2) / len(imgpoints2)   # 平均平方误差（重投影误差）
    tot_error += error
# print(ret, (tot_error / len(op))**0.5)
# cv2.namedWindow('winname', cv2.WINDOW_NORMAL)
# cv2.imshow('winname', a)
# cv2.waitKey(0)
"""下面是校正部分"""
h, w = a.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (h, w), 1) # 校正内参矩阵
dst = cv2.undistort(a, mtx, dist, None)
# undistort
mapx, mapy = cv2.initUndistortRectifyMap(mtx, dist, None, newcameramtx, (w, h), 5)  # 用于计算畸变映射
dst = cv2.remap(a, mapx, mapy, cv2.INTER_LINEAR)    # 把求得的映射应用到图像上
# crop the image
# x, y, w, h = roi
# dst = dst[y:y + h, x:x + w]
# print(mapx.shape)
# print(mapy)
np.savez("outfile", mtx, dist)
a = cv2.cvtColor(a, cv2.COLOR_BGR2RGB)
dst = cv2.cvtColor(dst, cv2.COLOR_BGR2RGB)
# print(roi)
plt.subplot(121), plt.imshow(a), plt.title('source')
plt.subplot(122), plt.imshow(dst), plt.title('undistorted')
plt.show()