人工智能基础-数学知识之线性代数（1）

说明：本篇博客出自湖南师范大学基础教育大数据研究与应用重点实验室

本篇博客为人工智能基础-数学知识之线性代数的第一部分内容，主要介绍了线性代数中向量的含义及一些基本运算、文本向量化的三种方法，内含python相关实现代码。本篇博客较为简单，请读者在学习的过程中，适当学习相关代码，领会其中思想。

一、向量

1.1 向量的含义

向量是指在坐标系中的有箭头的线段。在线性代数中，向量经常以原点作为起点。
用行的方式排列的向量叫作行向量，用列的方式排列的向量叫作列向量。习惯上，我们说向量时都是指列向量，如果是行向量，会加上一个上标符号T， T代表转置。

–	行向量	列向量
示例	$$\mathbf{\alpha }=(2,4,6)$$	$$\begin{gathered} \mathbf{\beta }=\left[\begin{array}{c} \\ 2\\ 4\\ 7\end{array}\right] \end{gathered}$$
列向量表示法	$${\mathbf{\alpha }}^T$$	$$\mathbf{\beta }$$

1.2 创建向量

NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。此处以Numpy为例进行演示。

# 创建向量，利用Numpy中的ndarray定义一个一维数组对象，就相当于创建了一个向量
import numpy as np
x=np.array([1,2,3,4,5])
y=np.array([2,5,6,3,2])
#结果为 [1 2 3 4 5]和 [2 5 6 3 2]

注意：如果两个向量的维数相同，并且对应元素相等，才说明两个向量相等。

#判断向量是否相等
np.all(x==y)
#结果为 False

1.3 向量的范数（模长）

向量的长度，也叫作向量的二范数、模长，其计算公式就是两点间欧氏距离公式，记作$$\begin{gathered} \Vert a\Vert =\left[\begin{array}{c} \\ {a}_1\\ a_2\\ ⋮\\ a_n\end{array}\right]=\sqrt{a_1^2+a_2^2+\cdots +a_n^2} \end{gathered}$$
可以利用Numpy中的linalg（线性代数）子模块进行运算：

#计算向量的长度
np.linalg.norm(x)
#结果为 7.416198487095663

1.4 向量加法（减法）

向量的加法（减法）就是两个维度相同的向量的对应元素之间的相加（减）。
$$\begin{gathered} \left[\begin{array}{c} \\ {a}_1\\ {\alpha }_2\end{array}\right]+\left[\begin{array}{c} \\ {b}_1\\ b_2\end{array}\right]=\left[\begin{array}{c} \\ {a}_1+b_1\\ a_2+b_2\end{array}\right] \end{gathered}$$
也可以从几何的角度理解向量的加减法运算：
将两个向量作为两条边，起点相同画一个平行四边形，对角线向量就是两个向量的和向量；两个向量的减法为平行四边形的另一条对角线。
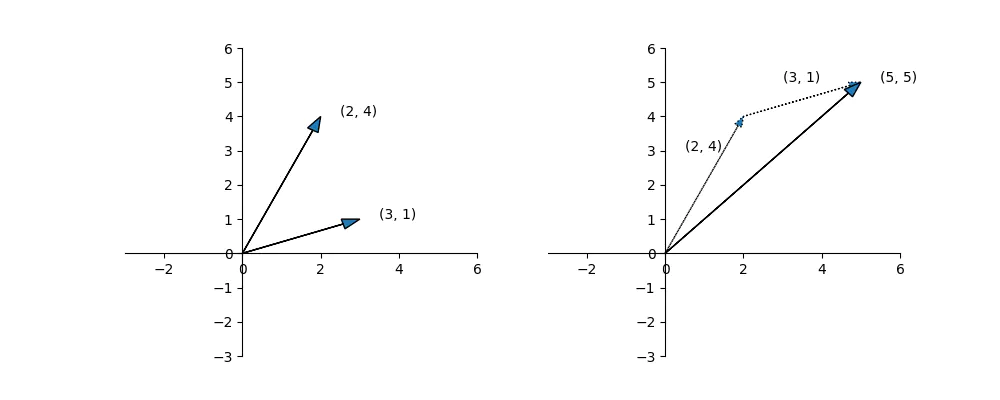在python中这样计算：

#向量减法，加法类似
z=x-y
#结果为 [-1 -3 -3  1  3]

1.5 向量的数乘

指向量与一个数字相乘，等于向量的各个分量都乘以相同的系数
$$\begin{gathered} \left[\begin{array}{c} \\ {a}_1\\ a_2\end{array}\right]\ast k=\left[\begin{array}{c} \\ {a}_1\ast k\\ a_2\ast k\end{array}\right] \end{gathered}$$
在python中这样计算：

#向量的数乘
z=10*x
#结果为 [10 20 30 40 50]

1.6 向量的乘法（点积）

指两个向量对应元素之积的和，得到的是一个数字。
$$\begin{gathered} \left[\begin{array}{c} \\ {a}_1\\ a_2\\ ⋮\\ a_n\end{array}\right].\left[\begin{array}{c} \\ {b}_1\\ b_2\\ ⋮\\ b_n\end{array}\right]=a_1{b}_1+a_2{b}_2\cdots +a_n{b}_n \end{gathered}$$
在python中这样计算：

#向量的点积，使用numpy.dot方法
np.dot(x,y)
#结果为 52

在数值上等于两个向量的长度和夹角余弦之积，即：
$$a\cdot b=||a||\ast ||b||\ast \cos \theta$$

二、向量化

文本向量化属于自然语言处理的范畴，在所有数据任务中，机器处理的都是全是数字的向量。文本向量化就是将文本表示成一系列能够表达文本语义的向量。
文本向量化主要有以下几种方法：

2.1 One-Hot Encoding方式

独热编码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。
大致步骤为：①分词②构造文本分词后的字典③对词语进行One-hot编码。

例如：
对于句子’I , I , I love study’和’study is my angle!’，首先将其看做为一篇文档，分词之后，构成字典包括’angle’, ‘i’, ‘is’, ‘love’, ‘my’, 'study’六个单词，再对每个句子进行分词，若句子中出现字典中的字，则记为1，否则记为0。最终得到编码表如下所示。

–	angle	i	is	love	my	study
I , I , I love study	0	1	0	1	0	1
study is my angle	1	0	1	0	1	1

代码如下：（此处为英文句子，英文句子默认会分词，而中文不会）

from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd

corpus=['I , I , I love study', 'study is my angle!']
vectorizer=CountVectorizer(min_df=1, binary=True, token_pattern='\w{1,}')
 # token_pattern：通过正则表达式来确定哪些数据被过滤掉，默认情况下单个英文字母会被过滤掉，代码中的\w{1,}可以避免这种情况
 
data=vectorizer.fit_transform(corpus)
print(vectorizer.get_feature_names())  # 特征名称
print(vectorizer.vocabulary_)             # 特征在列表中的索引位
print(data)
df = pd.DataFrame(data.toarray(), columns=vectorizer.get_feature_names()) # to DataFrame
print(df.head())

得到结果如下：

['angle', 'i', 'is', 'love', 'my', 'study'] #获取到的特征，这里为一个一个的单词
{
     'i': 1, 'love': 3, 'study': 5, 'is': 2, 'my': 4, 'angle': 0} #各个特征的索引号，例如‘i’：1 表示字符i在特征表中的索引为 1
#得到稀疏矩阵。比如(0,5) 1  表示在全部矩阵的第0行第5列有数据1，在稀疏矩阵中没有表示的索引全部为0
  (0, 5)	1
  (0, 3)	1
  (0, 1)	1
  (1, 0)	1
  (1, 4)	1
  (1, 2)	1
  (1, 5)	1
 #以下为最终的编码表
   angle  i  is  love  my  study
0      0  1   0     1   0      1
1      1  0   1     0   1      1

2.2 词袋（BOW）模型

词袋模型(Bag-of-words model，BOW)，BOW模型假定对于一个文档，忽略它的单词顺序和语法、句法等要素，将其仅仅看作是若干个词汇的集合，文档中每个单词的出现都是独立的，不依赖于其它单词是否出现。
与独热编码不同的是，词袋模型要把文章中所有单词的向量做加法运算，相当于记录每个单词的出现频次。依旧使用之前的例子，利用词袋模型得到的编码为：

–	angle	i	is	love	my	study
I , I , I love study	0	3	0	1	0	1
study is my angle	1	0	1	0	1	1

代码如下：

from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd

corpus=['I , I , I love study', 'study is my angle!']
# 将binary参数设置为False，表示不需要二值化
vectorizer=CountVectorizer(min_df=1, binary=False, token_pattern='\w{1,}')
 
data=vectorizer.fit_transform(corpus)
print(vectorizer.get_feature_names())  # 特征名称
print(vectorizer.vocabulary_)             # 特征在列表中的索引位
print(data)
df = pd.DataFrame(data.toarray(), columns=vectorizer.get_feature_names()) # to DataFrame
print(df.head())

最终得到结果：

['angle', 'i', 'is', 'love', 'my', 'study']
{
     'i': 1, 'love': 3, 'study': 5, 'is': 2, 'my': 4, 'angle': 0}
  (0, 5)	1
  (0, 3)	1
  (0, 1)	3
  (1, 0)	1
  (1, 4)	1
  (1, 2)	1
  (1, 5)	1
   angle  i  is  love  my  study
0      0  3   0     1   0      1
1      1  0   1     0   1      1

2.3 TF-IDF

TF-IDF（term frequency–inverse document frequency）是一种用于信息检索与数据挖掘的常用加权技术。TF意思是词频(Term Frequency)，IDF意思是逆文本频率指数(Inverse Document Frequency)。
字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。一个词语在一篇文章中出现次数越多, 同时在所有文档中出现次数越少, 越能够代表该文章。
一个词x的IDF值公式如下：
$$IDF(x)=log\frac{N}{N(x)}$$
其中N代表语料库中文本的总数，而N(x)代表语料库中包含词x的文本总数。
上面的IDF公式已经可以使用了，但是在一些特殊的情况会有一些小问题，比如某一个生僻词在语料库中没有，这样我们的分母为0， IDF没有意义了。所以常用的IDF我们需要做一些平滑，使语料库中没有出现的词也可以得到一个合适的IDF值。平滑的方法有很多种，最常见的IDF平滑后的公式之一为：
$$IDF(x)=log\frac{N}{N(x)+1}$$
代码如下：

from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer

corpus=["I like to travel","I love tea"]

vectorizer=CountVectorizer(min_df=1, binary=False, token_pattern='\w{1,}')

transformer = TfidfTransformer()
tfidf = transformer.fit_transform(vectorizer.fit_transform(corpus))
print(tfidf)
df = pd.DataFrame(tfidf.toarray(), columns=vectorizer.get_feature_names()) # to DataFrame
print(df.head())

结果如下，可以明显看到 i 的值较其他值是较低的：

  (0, 0)	0.37997836159100784
  (0, 1)	0.534046329052269
  (0, 4)	0.534046329052269
  (0, 5)	0.534046329052269
  (1, 0)	0.4494364165239821
  (1, 2)	0.6316672017376245
  (1, 3)	0.6316672017376245
          i      like      love       tea        to    travel
0  0.379978  0.534046  0.000000  0.000000  0.534046  0.534046
1  0.449436  0.000000  0.631667  0.631667  0.000000  0.000000

或者使用用TfidfVectorizer一步到位，代码如下：

from sklearn.feature_extraction.text import TfidfVectorizer
tfidf2 = TfidfVectorizer(token_pattern='\w{1,}')
re = tfidf2.fit_transform(corpus)
print(re)

结果与第一种的输出完全相同。

2.4 三种方法的缺点

较为明显地可以看到，以上三种文本向量化的方式或多或少存在着以下缺点：

–	缺点
One-hot编码	①维数过高，随着语料的增加，维数会越来越大，导致维数灾难；②矩阵稀疏，从上面也可以看到，每一个词向量只有1维是有数值的，其他维上的数值都为0；③不能保留语义。用这种方式得到的结果不能保留词语在句子中的位置信息。
词袋（BOW）模型	①不能保留语义；②矩阵稀疏
TF-IDF	不能保留语义,无法处理一词多义与一义多词的情况

上述三种方法最大的缺点就是单词的编码不能体现词义，对于任何两个单词向量而言，它们的夹角余弦相似度都是0，无法体现词义之间的关系，因此，谷歌提出了Word2Vec，可以在一定程度上解决这个问题，关于这个问题，我们下一篇博客详细讨论。

欢迎大家在评论区提出自己对本篇博客的看法和建议，有问题可留言或私戳我~

---

参考文献

[1] 张晓明.人工智能基础——数学知识.北京:人民邮电出版社.2020.
[2] https://www.cnblogs.com/dogecheng/p/11470196.html
[3] https://blog.csdn.net/Clannad_niu/article/details/95216996