雷达信号处理---线性调频信号脉冲压缩MATLAB实现
关于脉冲压缩的原理以及公式推导这里不再赘述,主要讲解如何通过MATLAB进行仿真。
实现原理
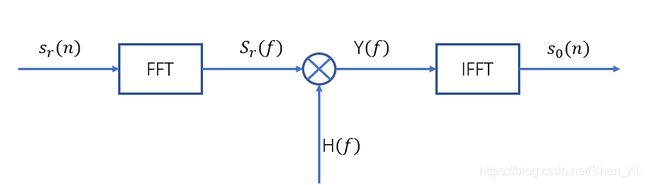
脉冲压缩是为了解决雷达作用距离与距离分辨率这一矛盾关系而产生的技术,普通雷达在提升雷达作用距离的同时,会使得距离分辨率下降许多,反之亦然。而脉冲压缩雷达发射的是大时宽带宽积的射频信号,这保证了雷达的作用距离;同时,接收端会对发射信号做脉冲压缩处理,得到形似sinc函数的信号,该信号具有很好的距离分辨能力。在接收端的具体实现过程如下图。
其中,![]() 是雷达回波信号,
是雷达回波信号,![]() 是脉冲压缩的输出信号,
是脉冲压缩的输出信号,![]() 是滤波器系数
是滤波器系数![]() 经傅里叶变换后的结果。由于脉冲压缩本质上是匹配滤波,故
经傅里叶变换后的结果。由于脉冲压缩本质上是匹配滤波,故![]() ,即发射信号反褶后去共轭。线性调频脉冲信号的发射信号可表示为
,即发射信号反褶后去共轭。线性调频脉冲信号的发射信号可表示为![]() 。
。
同时,经过公式推导,可以知道,经过匹配滤波后,最大的旁瓣仅比主瓣电平小-13.2dB,在检测多个目标时,强目标回波的旁瓣有可能会淹没弱信号的主瓣,导致信号丢失。故,我们可以利用窗函数来抑制旁瓣。
现在从时域,频域分别讨论脉冲压缩实现方法。
时域脉冲压缩
方法一
发射信号反褶,取共轭后与发射信号做卷积处理 ,得到脉冲压缩信号。适用于脉压比要求小时的情况。(脉压比是输入脉冲与输出脉冲的宽度之比)
out =conv(conj(fliplr(s)), sr);%s为发射信号,sr为目标回波信号方法二
由于![]() ,故
,故![]() 。脉冲压缩信号
。脉冲压缩信号![]() ,可得
,可得![]() 。即匹配滤波也可表示为回波信号与发射信号的互相关。
。即匹配滤波也可表示为回波信号与发射信号的互相关。
out =xcorr(s, sr);%s为发射信号,sr为目标回波信号频域脉冲压缩
方法一
发射信号时间反褶,取共轭后,计算FFT,再与经过FFT处理的回波信号在频域相乘,最后IFFT取得时域脉冲压缩信号。
out =ifft(fft(sr,n).*fft(conj(fliplr(s)),n),n);%s为发射信号,sr为目标回波信号方法二
发射信号做FFT变换后,取共轭。再与经过FFT处理的回波信号在频域相乘,最后IFFT取得时域脉冲压缩信号。
out =ifft(fft(sr,n).*conj(fft(s,n)),n);%s为发射信号,sr为目标回波信号测距仿真
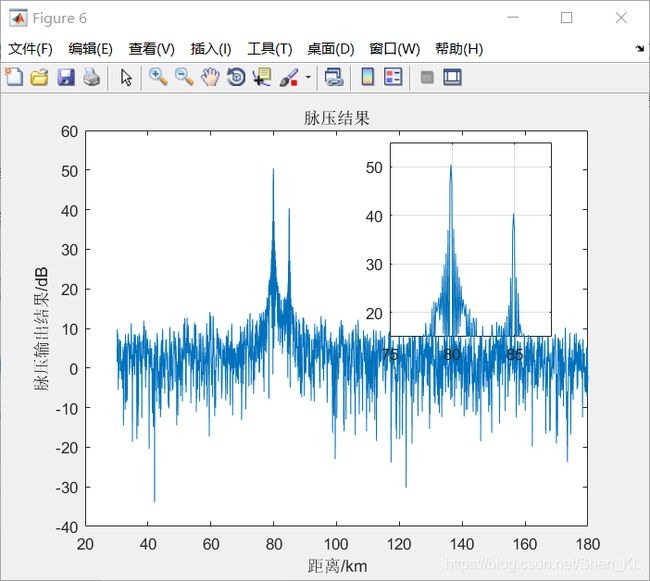
现在假设目标分别距离为80km,85km,使用线性调频脉冲压缩信号对目标进行测距。脉冲宽度![]() 为
为 ![]() ,调频带宽
,调频带宽![]() 为
为![]() ,采样时钟
,采样时钟![]() 为
为![]() ,信噪比SNR分别为20dB,10dB,采样的最小距离
,信噪比SNR分别为20dB,10dB,采样的最小距离![]() 为20km,距离窗
为20km,距离窗![]() 为150km,波数
为150km,波数![]() 为
为![]()
仿真结果如下
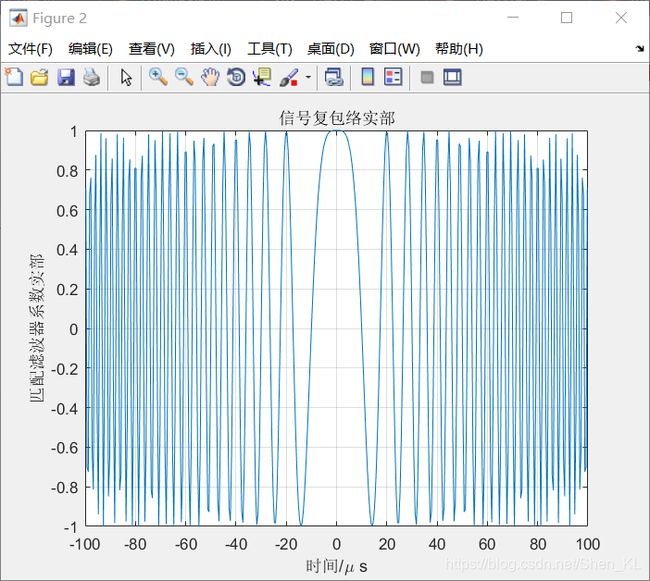
| 线性调频脉冲信号 复包络实部 |
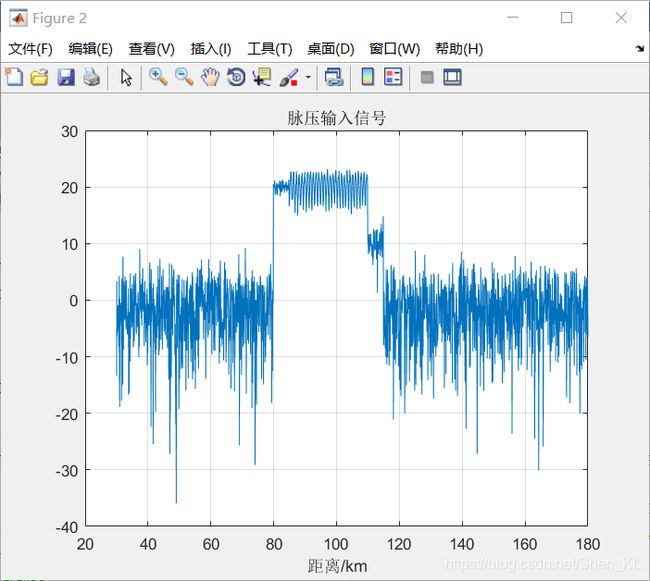
脉压输入信号 | 脉压输出信号 |
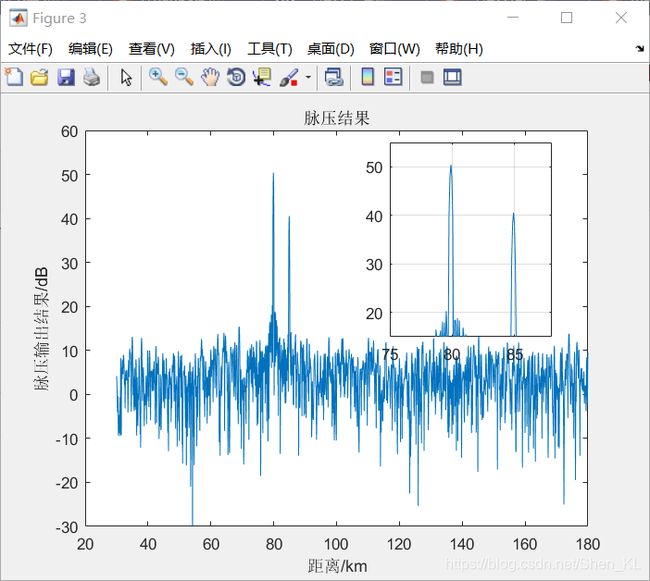
| 未加窗结果 | 加窗结果 |
仿真程序如下
%产生线性调频脉冲的目标回波信号,并给出脉压结果
%Tp发射脉冲宽度s,Bm调频带宽Hz,Ts采样时钟s,R0目标的距离矢量m,Vr目标速度矢量m/s,SNR目标信噪比矢量dB,Rmin采样最小距离,Rrec距离窗的大小(雷达探测最大最小作用距离的差值),Window窗函数,bos波数
%本例将两个物体都设定为静止 若改变Vr 可验证距离-多普勒测不准原理
%图三可以看到在80 85km处有脉冲信号
clear all;clc;
Tp=200e-6;Bm=1e6;Ts=0.5e-6;R0=[80e3,85e3];Vr=[0,0];SNR=[20,10];Rmin=30e3;Rrec=150e3;Window=taylorwin(Tp/Ts);bos=2*pi/0.03;
mu=Bm/Tp;%调频率
c=3e8;
M=round(Tp/Ts);%round函数取整数
t1=(-M/2+0.5:M/2-0.5)*Ts;%时间矢量
NR0=ceil(log2(2*Rrec/c/Ts+M));%ceil函数朝正无穷大四舍五入 2*Rrec/c/Ts为距离窗的单元数
NR1=2^NR0;%以上两步 模拟补零,将N拓展为2的幂!!!!!
lfm=exp(1i*pi*mu*t1.^2);%线性调频信号 单脉冲
W_t=lfm.*Window.';%加窗 抑制旁瓣
game=(1+2*Vr./c).^2;
sp=(0.707*(randn(1,NR1)+1i*randn(1,NR1)));%噪声
for k=1:length(R0)
NR=fix(2*(R0(k)-Rmin)/c/Ts);%fix函数 让变量向0靠近取整 NR代表的是距离为R0的物体的回波在时间轴上的位置
spt=(10^(SNR(k)/20))*exp(-1i*bos*2*(R0(k)-Vr(k)*t1)).*(exp(1i*pi*mu*game(k)*(t1).^2));%10^(SNR(k)/20)是将dB值换算回原单位
sp(NR:NR+M-1)=sp(NR:NR+M-1)+spt;%信号+噪声
end;
spf=fft(sp,NR1);Wf_t=fft(W_t,NR1);
y=abs((ifft(spf.*conj(Wf_t),NR1)/NR0));%conj 取复共轭
N0=2*(Rrec)/c/Ts;
t=linspace(Rmin/1000,(Rmin+Rrec)/1000,N0);
figure;plot(t,20*log10(abs(sp(1:N0))));xlabel('距离/km');title('脉压输入信号'); grid;%脉压输入信号
figure;plot(t1*1e6,real(lfm));xlabel('时间/\mu s');ylabel('匹配滤波器系数实部');title('信号复包络实部');grid;%线性调频信号复包络的实部
figure;plot(t,20*log10(y(1:N0)));xlabel('距离/km');ylabel('脉压输出结果/dB');title('脉压结果');%axis([30 180 -10 60]);grid;%脉压输出信号
h2=axes('Position',[0.6 0.5 0.25 0.4]);%在原图上绘制局部放大图 axes('Position',[subNormalxLabel,subNormalyLabel,normalWidth,normalHeight])
axes(h2); % 将h2设置为当前坐标系
plot(t,20*log10(y(1:2000)));%绘制局部图
set(h2,'xlim',[75 88]);
set(h2,'ylim',[15 55]);
grid;%显示网格
补充:
1.匹配滤波器接受的信号复包络不仅仅是发射信号的延时。实际上还有一个附加相移![]() (针对静止物体)
(针对静止物体)
2.脉冲压缩过程中,进行FFT的点数是有要求的。根据奈奎斯特采样定理,对实信号,采样信号 ![]() 。而对于时宽为
。而对于时宽为![]() 的LFM信号,其FFT的频率分辨率
的LFM信号,其FFT的频率分辨率![]() 应当小于等于
应当小于等于![]() ,那么需要的最小样本数应当为(FFT分辨率
,那么需要的最小样本数应当为(FFT分辨率![]() )
)
即最少需要![]() 个样本才能完全描述一个时宽为
个样本才能完全描述一个时宽为![]() 的LFM波形。
的LFM波形。
同时,我们还需要考虑距离窗内的距离单元数个数,具体求法为 ![]() 。
。
故,所需FFT的点数为![]()