八大排序算法(原理+代码详解)Python版
一、前言:
排序算法是最经典的算法知识,往往面试题中或数据结构中会涉及有关排序的算法,掌握排序算法的思想及其原理有助于化解排序方面的难题。
下面介绍几种Python语言中常见的排序算法:
冒泡排序、选择排序、插入排序、归并排序、快速排序、希尔排序、计数排序。
目录
一、前言:
二、排序算法
(一)冒泡排序
<1>简单介绍
<2>.算法描述:
<3>.代码部分
(二)选择排序
<1>简单介绍
<2>算法描述
<3>.代码部分
(三)插入排序
<1>简单介绍
<2>算法描述
<3>代码部分
(四)归并排序
<1>简单介绍
<2>算法描述
<3>代码部分
(五)快速排序(挖坑填数)
<1>简单介绍
<2>算法描述
<3>代码实现
(六)希尔排序(缩小增量排序)
<1>简单介绍
<2>算法描述
<3>代码部分
(七)计数排序
<1>简单介绍
<2>算法描述
<3>代码部分
二、排序算法
(一)冒泡排序
<1>简单介绍
冒泡排序(Bubble Sort) 是最为简单的一种排序,从第一个元素开始往后两两比较,把较大的元素交换到后面,第一轮比较结束后,最大的元素便放到了最后;然后从第二个元素开始往后两两比较,最终次大的元素便放在了倒数第二个位置.....,直到整个数组排好顺序。因如同气泡般往上浮,故交冒泡排序。-----------------------核心思想:通过元素来找位置,元素大的放在后面。
<2>.算法描述:
1.比较相邻两个元素,如果前者比后者大,便交换两个数的位置
2.对每一个相邻的元素做上述的操作,当一轮循环结束后,最大的元素便在最后
3.对所有的元素进行上面两个步骤,直到还剩最后一个元素为止(剩下的最后的一个元素,说明它已最小,不用交换)
4.重复1-3的步骤,直至循环退出
原理图:
<3>.代码部分
"""冒泡排序 通过元素来找位置"""
sortList=[8,2,3,1,2,6]
for i in range(0,len(sortList)-1):
for j in range(0,len(sortList)-1-i):
if sortList[j]>sortList[j+1]:
"""异或运算符,对两元素进行交换"""
sortList[j],sortList[j+1] = sortList[j+1],sortList[j]
print(sortList)(二)选择排序
<1>简单介绍
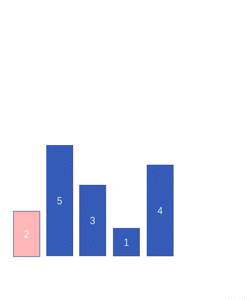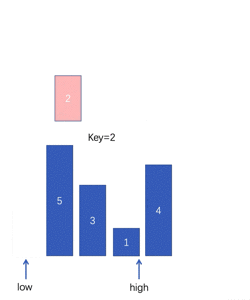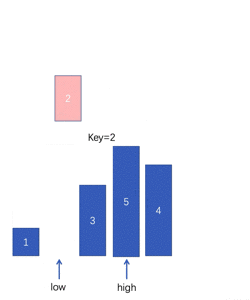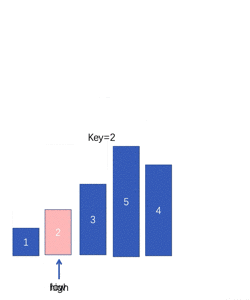
选择排序(Select Sort) 即每一趟从待排序的数据元素中选出最小(最大)的元素,顺序放在待排序的数列最前,直到全部待排序的数据元素全部排完。-----------核心思想:通过位置来找元素
<2>算法描述
1.在一个长度为N-1的无序数组中,第一次遍历N-1个数找到最小的元素,记录该元素的下标,当第一轮遍历结束时,通过下标所对应的元素与第一位置的元素的交换
2.第二次从下一个数开始遍历N-2个数,找到最小的元素,按照1的操作,将此元素与第二个位置的元素交换
3.重新以上操作,直到排序完成。
原理图:
<3>.代码部分
"""选择排序 位置来找元素"""
sortList = [2,1,5,3,5,6,8]
for i in range(0,len(sortList)-1):
"""通过定义一个变量index 来记录 此时需排序的位置"""
index=i
for j in range(i+1,len(sortList)):
if(sortList[index]>sortList[j]):
index=j
"""循环结束 让最小的元素与相应位置上的元素进行交换"""
sortList[index],sortList[i]=sortList[i],sortList[index]
print(sortList)(三)插入排序
<1>简单介绍
插入排序是一种最简单直观的排序算法,通过构建有序的元素,对于未排序的元素,在已经排好序的元素中从后往前查找,找到相应位置并插入,直到所有待排序元素元素全部插入为止。
<2>算法描述
1.从第二个元素开始从后往前遍历,若未排序的元素比排完序的元素小,则排完序的元素往后移动,未排序的元素往前移(通过交换元素实现移动)
2.第三个元素同理,若比前面最近的元素(已排完序)大,则不动
3.重复1-2的步骤,直到最后一个元素插入成功
<3>代码部分
插入排序
def insert_sort(relist):
# range() 前闭后开 从第二个元素开始
for i in range(1,len(relist)):
'''从后往前开始依次遍历 若未排序的元素比排完序的元素小,
则排完序的元素往后移动,未排序的往前移'''
for j in range(i,0,-1):
if relist[j] <= relist[j-1]:
relist[j],relist[j-1] = relist[j-1],relist[j]
print(relist)
relist = [8,3,2,6,1,4,9,7]
insert_sort(relist)原理图:
(四)归并排序
<1>简单介绍
归并排序,是创建在归并操作上的一种有效的排序算法,该算法的基本思想是采用分治法,一般用于总体上无序,单各个子项相对有序的元素。
<2>算法描述
直接上图:
此图展示了归并算法的核心思想,其中箭头旁边的序号表示执行的顺序,其思路为:
1.把整个数组尽可能分为相等的两个部分------体现 “分” 的思想,即递的过程
2.最终把数组分成一个一个元素后,开始返回,即归的过程
3.对于两个被分开的两个部分进行整个的递归排序--------“治”
4.最后把两个被分开的且已排好序的数组拼接在一起
原理图:
<3>代码部分
# 归并排序
def merge_sort(ary):
# 当传的列表元素为1时 开始归来(此条件作为递归出口)
if len(ary) <= 1:
return ary
median = int(len(ary)/2) # 二分分解 一直分解到每组只有一个元素为止
"""按顺序执行,先执行左边的元素的切割,再执行右边元素的切割"""
left = merge_sort(ary[:median])#切片前闭后开
right = merge_sort(ary[median:])
"""从最低层开始合并,从下往上的过程 ------归来"""
return merge(left, right) # 合并数组,从最底层开始
def merge(left, right):
'''合并操作,
将两个有序数组left[]和right[]合并成一个大的有序数组'''
new = []
i = j = k = 0
# 循环比较两个数列的数值大小,把小的元素存放到new列表中
while(i < len(left) and j < len(right)):
if left[i] < right[j]:
new.append(left[i])
i += 1
else:
new.append(right[j])
j += 1
"""拼接多余的元素"""
new = new + left[i:] + right[j:]
return new
print(merge_sort([1,2,1,3,2,4,5,3,4,9,7,6]))(五)快速排序(挖坑填数)
<1>简单介绍
快速排序使用了分而治之的思想,是冒泡排序的一种改进。即把大的序列拆分成小的序列,然后小的再拆分为更小的。实现原理:从当前序列中选择一个元素作为基准数,通过一轮的比较,把比基准数大的元素放在左边,比基准数小的放在右边,然后对这两部分分别进行上述同样的操作,直到整个序列有序为止。
<2>算法描述
1.从序列中选出一个基准数(),定义好指向序列首尾两端的两个指针(此时指针我们用下标来表示)
2.先从右下标开始查找比基准数小的元素,若下标所指向的元素 比基准数 大,则向左进一位,继续比较 直到存在比基准数小的为止,此时便把该元素填入左下标所指向的元素(做下标第一次指向的是基准数)
3.完成 2号步骤后, 左下标需向右进一位,然后左下标进行 2号步骤类似的操作,想右遍历,查找比基准数大的元素,找到后便把此元素填入右下表所指向的元素(注意:右下标的值已保存在左边,所以可以直接覆盖),同理 填完后右下标相应向左移动一位,准备下一轮的操作。
4.反复执行2号和3号的操作,直至左右两下标重合,便把基准元素填入下标重合位置处,此时 基准数左右两边便完成了右边小 左边大的情况。
5.对左右两个区域单独进行上述的操作,直到区域元素个数为1为止。
原理图:
<3>代码实现
# 快速排序
def quick_sort(alist, first, last):
"""快速排序"""
if first >= last:
return
"""选取基准元素 == 挖出基准元素"""
mid_value = alist[first]
"""定义两个 下标 (指针) 指向数列两端"""
low = first
high = last
while low < high:
while low < high and alist[high] >= mid_value:
high -= 1
""" 打破循环的条件是 左边的下标所指向的元素小于基准元素"""
if low < high:
alist[low] = alist[high]
""" 赋完值后下标右进一位"""
low+=1
while low < high and alist[low] < mid_value:
low += 1
"""打破循环的条件 是右边的下标所指向的元素大于基准元素"""
if low(六)希尔排序(缩小增量排序)
<1>简单介绍
希尔排序也是一种插入排序,是简单插入排序经过改进后的一个更高效的版本。通过比较一定间隔的元素进行插入排序,同时不断缩小间隔(增量),直到比较相邻元素。当增量为0时,算法终止。
<2>算法描述
先上图:
1、动态图中,颜色相同的为一组,序列共有10个元素,增量gap=length/2 ,即第一遍的时候增量为5,共分为5组,在每组中进行简单的插入排序,在组内实现元素的排序。
2、第二遍的时候 增量(gap=gap/2)便为2,其余操作与1相同
3、当gap=1时 此时便是整个序列为一组,对整个序列进行插入排序即可。
<3>代码部分
# # 希尔排序(缩小增量排序)
def shell_sort(ary):
# 增量分配
gap=round(len(ary)/2)
# 当(增量)gap=1时 整个文件恰被分成一组,gap=0时算法终止
while gap>=1:
"""从后半部分开始遍历 即每组进行插入排序"""
for i in range(gap,len(ary)):
while i-gap >= 0 and ary[i-gap]>ary[i]:
ary[i],ary[i-gap]=ary[i-gap],ary[i]
i-=gap
"""再次缩小增量"""
gap = round(gap/2)
return ary
print(shell_sort([1,3,5,2,4,3,6,4,3,7]))(七)计数排序
<1>简单介绍
计数排序是一个不基于比较的一个排序算法,对于其它需比较的算法而言,它的速度更快。但是一种以空间换取时间的算法,需额外开辟存放排序后的数列。
<2>算法描述
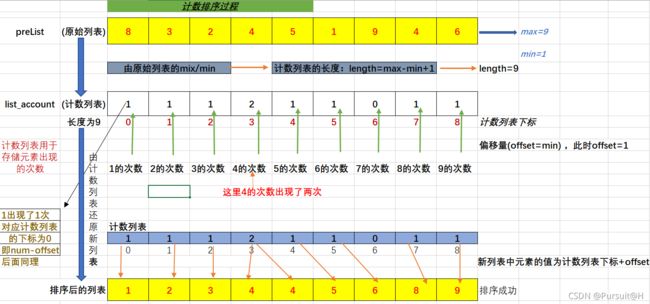
用excel表绘制的计数排序过程如下:
算法步骤:
1、找出待排序数组的最大和最小值,求出偏移量offset = min
2、定义计数列表,且长度为length = max-min+1
3、统计数组中每个元素出现的次数,并存放到计数列表中(为了方便计数列表的统计,我们将需统计的元素值做个变形:元素值-偏移量,此时刚好对应计数列表的下标,对应下标-1即可)-------还原时下标+1便可还原为元素自身的大小。
4、最后还原序列,只需要以计数列表中统计的个数遍历还原即可-----注意元素大小需要下标+1哦!
最后,配一张动态图,有助于对原理的理解:
PS:此图来源于网络(侵删)
<3>代码部分
# 计数排序:
preList = [4,2,5,3,7,3,7,2,6]
maxsize = max(preList)
minsize = min(preList)
len_account = maxsize-minsize+1
offset = minsize
# 计数列表
list_account = [0]*len_account
# 初始化排序后的列表
laterList = [0]*len(preList)
for num in preList:
list_account[num-offset]+=1 #列表的初值都为0 可以直接用下标进行加减运算
index = 0
for i in range(0,len_account):
# 计算列表中 数值为几 就循环几遍
for j in range(0,list_account[i]):
laterList[index]=i+offset
index +=1
print("")
print(laterList)以上排序算法由个人总结,如有不足之处,欢迎大家指正!