【python数据结构】树和二叉树
目录
树的逻辑结构
树的定义
树的基本术语
树的遍历操作
前序遍历
后序遍历
层序遍历
树的存储结构
双亲表示法
孩子链表表示法
双亲孩子表示法
孩子兄弟表示法
二叉树的逻辑结构
二叉树的特点
特殊的二叉树
斜树
满二叉树
完全二叉树
二叉树的基本性质
完全二叉树的基本性质
二叉树的遍历操作
前序(根)遍历:A B D G C E F
中序(根)遍历:D G B A E C F
后序(根)遍历:G D B E F C A
层序遍历:A B C D E F G
树结构是非常重要的一种非线性结构,具有严格的层次特征。
(树是一对多,而二叉树是一对二)
树的逻辑结构
树的定义
n(n≥0)个结点的有限集合。当n=0时,称为空树;任意一棵非空树满足以下条件:
- 有且仅有一个特定的称为根的结点;
- 当n>1时,除根结点之外的其余结点被分成m(m>0)个互不相交的有限集合T1,T2,… ,Tm,其中每个集合又是一棵树,并称为这个根结点的子树。
- 树的定义是采用递归方法
树的基本术语
结点的度:结点所拥有的子树的个数。
树的度:树中各结点的最大值。
叶子结点:度为0的结点,也称为终端结点。
分支结点:度不为0的结点,也称为非终端结点。
孩子、双亲:树中某结点子树的根结点称为这个结点的孩子结点,这个结点称为它孩子结点的双亲结点;
兄弟:具有同一个双亲的孩子结点互称为兄弟。
路径:如果树的结点序列n1,n2,…,nk有如下关系:路径上经过的边的个数称为路径长度。
祖先、子孙:在树中,如果有一条路径从结点x到结点y,则x称为y的祖先,而y称为x的子孙。
结点所在层数:根结点的层数为1;对其余任何结点,若某结点在第K曾,则其孩子结点在第K+1曾。
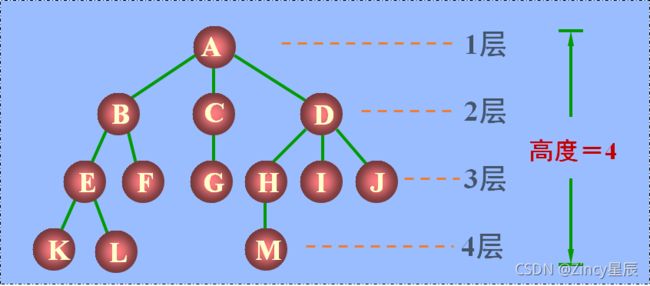
树的深度:树中所有结点的最大层数,也称高度。
层序编号:将树中的结点按照从上层到下层、同曾从左到右的次序依次给他们编以从1开始的连续自然数。
有序树、无序树:如果一棵树中结点的各子树从左到右是有次序的,称这棵树为有序树;反之,称为无序树。
森林:m(m≥)0棵互不相交的树的集合。
树的遍历操作
树的遍历:从根结点出发,按照某种次序访问树中所有结点,使得每个结点被访问一次且仅被访问一次。
树的访问:抽象操作,可以是对结点进行的各种处理,这里简化为输出结点的数据。
遍历的实质:树结构(非线性结构)→线性结构。
次序:通常有前序(根)遍历、后序(根)遍历和层序(次)遍历三种方式。
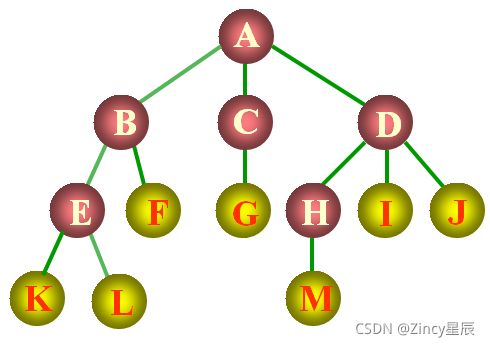
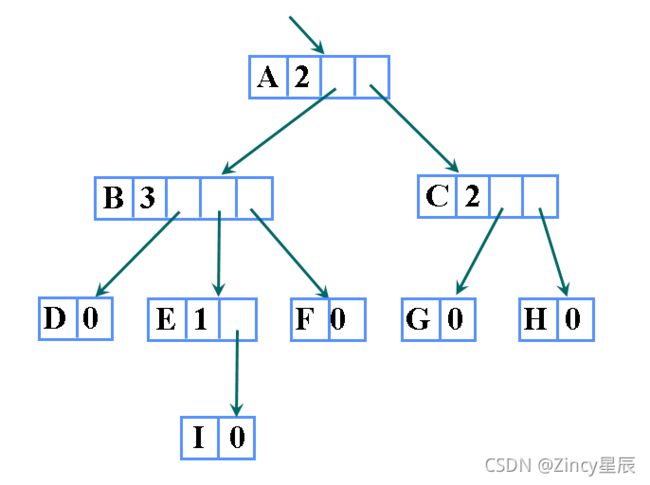
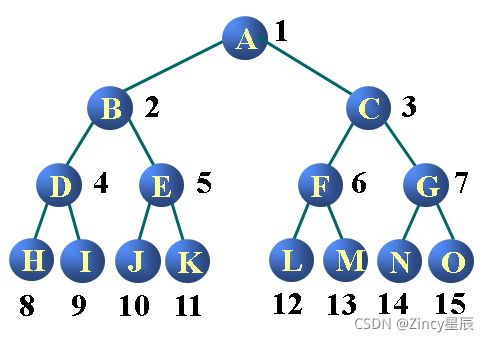
以这个树为例:
前序遍历
树的前序遍历操作定义为:若树为空,则空操作返回;否则
⑴ 访问根结点;
⑵ 按照从左到右的顺序前序遍历根结点的每一棵子树。
前序遍历序列:A B D E H I F C G
后序遍历
树的后序遍历操作定义为:若树为空,则空操作返回;否则
⑴ 按照从左到右的顺序后序遍历根结点的每一棵子树;
⑵ 访问根结点。
后序遍历序列:D H I E F B G C A
层序遍历
树的层序遍历操作定义为:从树的第一层(即根结点)开始,自上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
层序遍历序列:A B C D E F G H I
树的存储结构
存储结构:数据元素以及数据元素之间的逻辑关系在存储器中的表示。
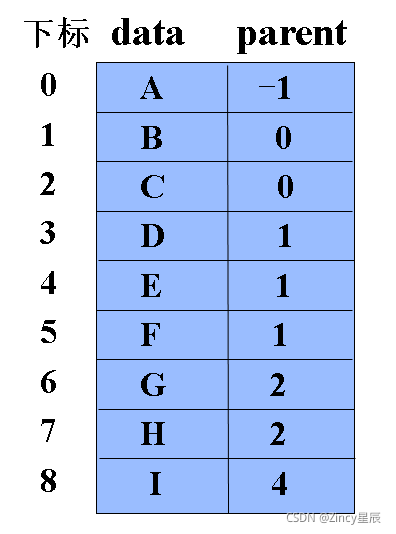
双亲表示法
基本思想:用一维数组来存储树的各个结点(一般按层序存储),数组中的一个元素对应树中的一个结点,包括结点的数据信息以及该结点的双亲在数组中的下标。
data:存储树中结点的数据信息
parent:存储该结点的双亲在数组中的下标
查找双亲结点(时间性能O1):
查找孩子结点(时间性能On):
查找兄弟结点(层序存储时时间性能为O1:
孩子链表表示法
链表中的每个结点包括一个数据域和多个指针域,每个指针域指向该结点的一个孩子结点。
方案一:指针域的个数等于树的度
其中:data:数据域,存放该结点的数据信息;
child1~childd:指针域,指向该结点的孩子。
缺点:浪费空间
 在一棵有n个结点、度为k的树中,必有n*(k-1) +1个空链域。 由n x k - (n-1)推导得出
在一棵有n个结点、度为k的树中,必有n*(k-1) +1个空链域。 由n x k - (n-1)推导得出
链表中的每个结点包括一个数据域和多个指针域,每个指针域指向该结点的一个孩子结点。
方案二: 指针域的个数等于该结点的度
其中:data:数据域,存放该结点的数据信息;
degree:度域,存放该结点的度;
child1~childd:指针域,指向该结点的孩子。
缺点:结点结构不一致
将结点的所有孩子放在一起,构成线性表。
孩子链表的基本思想:把每个结点的孩子排列起来,看成是一个线性表,且以单链表存储,则n个结点共有 n 个孩子链表。这 n 个单链表共有 n 个头指针,这 n 个头指针又组成了一个线性表,为了便于进行查找采用顺序存储。最后,将存放 n 个头指针的数组和存放n个结点的数组结合起来,构成孩子链表的表头数组。
查找孩子:时间
查找孩子的时间性能较好,查找双亲的时间性能不好
双亲孩子表示法
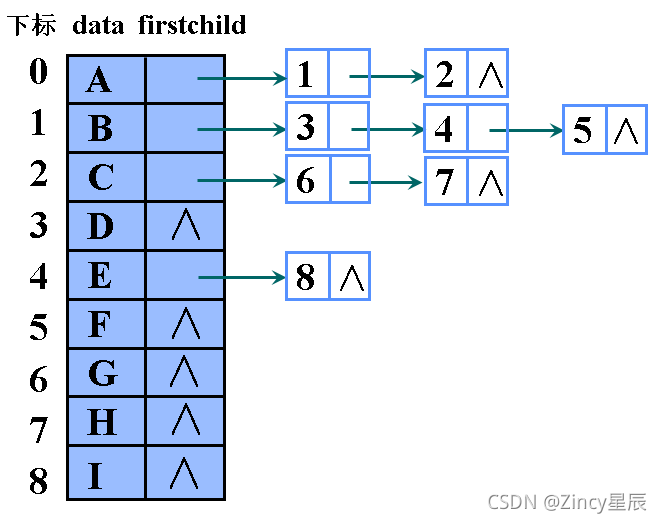
孩子兄弟表示法
某结点的第一个孩子是惟一的,右兄弟是惟一的。设置两个分别指向该结点的第一个孩子和右兄弟的指针。
data:数据域,存储该结点的数据信息;
firstchild:指针域,指向该结点第一个孩子;
rightsib:指针域,指向该结点的右兄弟结点。
查找孩子的时间性能较好(O1),查找双亲的时间性能不好
二叉树的逻辑结构
二叉树是n(n≥0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
问题转化:将树转换为二叉树,从而利用二叉树解决树的有关问题。
二叉树的特点
⑴ 每个结点最多有两棵子树;
⑵ 二叉树是有序的,其次序不能任意颠倒。
注意:二叉树和树是两种树结构。
 特殊的二叉树
特殊的二叉树
斜树
1 .所有结点都只有左子树的二叉树称为左斜树;
2 .所有结点都只有右子树的二叉树称为右斜树;
3.左斜树和右斜树统称为斜树。
斜树的特点:
1. 在斜树中,每一层只有一个结点;
2. 斜树的结点个数与其深度相同。
满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上。
满二叉树的特点:
1.叶子只能出现在最下一层;2.只有度为0和度为2的结点。
满二叉树在同样深度的二叉树中结点和叶子结点个数都最多
下面是一个不是满二叉树例子:虽然所有分支结点都有左右子树,但叶子不在同一层上。(但是按英文定义,这是full binary tree,每个分支结点度为2)
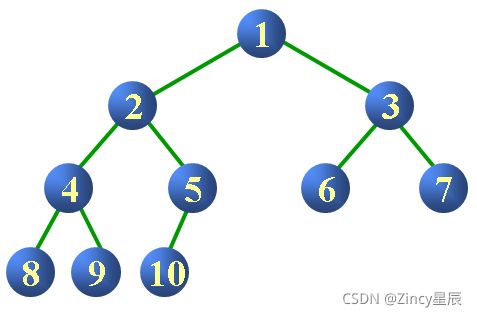
完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同。
在满二叉树中,从最后一个结点开始,连续去掉任意个结点,即是一棵完全二叉树。
完全二叉树的特点:
1. 叶子结点只能出现在最下两层且最下层的叶子结点都集中在二叉树的左面;
2. 完全二叉树中如果有度为1的结点,只可能有一个,且该结点只有左孩子。
3. 深度为k的完全二叉树在k-1层上一定是满二叉树。
4. 在同样结点个数的二叉树中,完全二叉树的深度最小。
下面是一个不是完全二叉树的例子:结点10与满二叉树中的结点10不是同一个结点。一个是左子树,一个是右子树。
二叉树的基本性质
- 二叉树的第i层上最多有2^(i-1)个结点(i ≥ 1)
- 一棵深度为k的二叉树中,最多有2^k -1个结点,最少有k个结点(深度为k且具有2k-1个结点的二叉树一定是满二叉树,深度为k且具有k个结点的二叉树不一定是斜树。)
- 在一棵二叉树中,如果叶子结点数为n0,度为2的结点数为n2,则有: n0=n2+1(n个结点的满二叉树叶子结点n0 = (n+1) /2 )
完全二叉树的基本性质
1.具有n个结点的完全二叉树的深度为 [ ] +
2.对一棵具有n个结点的完全二叉树中从1开始按层序编号,则对于任意的序号为i(1≤i≤n)的结点(简称为结点i),有:
(1)如果i>1,则结点i的双亲结点的序号为i/2;如果i=1,则结点i是根结点,无双亲结点。
(2)如果2i ≤ n,则结点i的左孩子的序号为2i;
如果2i >n,则结点i无左孩子。
(3)如果2i+1 ≤ n,则结点i的右孩子的序号为2i+1;
如果2i+1 >n,则结点i无右孩子。
对一棵具有n个结点的完全二叉树中从1开始按层序编号,则
- 结点i的双亲结点为 i/2
- 结点i的左孩子为2i
- 结点i的右孩子为2i+1
在完全二叉树中,结点的层序编号反映了结点之间的逻辑关系
二叉树的遍历操作
二叉树的遍历是指从根结点出发,按照某种次序(前序遍历、中序遍历、后序遍历、层序遍历
)访问二叉树中的所有结点,使得每个结点被访问一次且仅被访问(抽象操作,可以是对结点进行的各种处理,这里简化为输出结点的数据)一次。
二叉树的组成:根结点D、左子树L、右子树R
二叉树的遍历方式:DLR、LDR、LRD、DRL、RDL、RLD
如果限定先左后右,则二叉树遍历方式有三种:前序:DLR、中序:LDR、后序:LRD
层序遍历:按二叉树的层序编号的次序访问各结点。
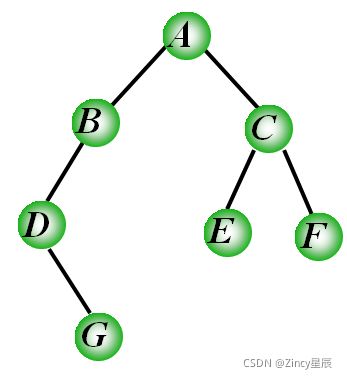
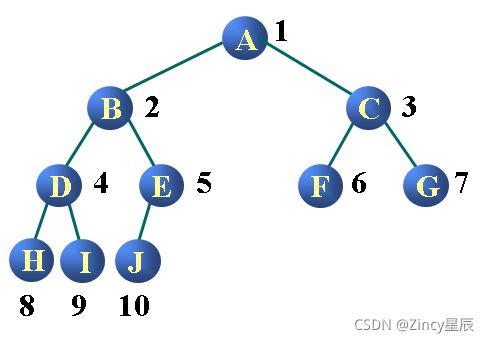
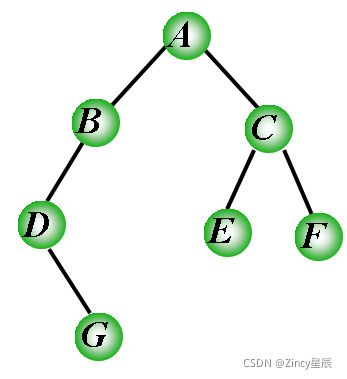
以这个二叉树为例:
前序(根)遍历:A B D G C E F
若二叉树为空,则空操作返回;否则:
①访问根结点;
②前序遍历根结点的左子树;
③前序遍历根结点的右子树。
中序(根)遍历:D G B A E C F
若二叉树为空,则空操作返回;否则:
①中序遍历根结点的左子树;
②访问根结点;
③中序遍历根结点的右子树。
后序(根)遍历:G D B E F C A
若二叉树为空,则空操作返回;否则:
①后序遍历根结点的左子树;
②后序遍历根结点的右子树;
③访问根结点。
层序遍历:A B C D E F G
二叉树的层次遍历是指从二叉树的第一层(即根结点)开始,从上至下逐层遍历,在同一层中,则按从左到右的顺序对结点逐个访问。