##智能优化算法复习

智能优化算法

#总述

智能优化算法分为进化类算法，群智能算法，以及模拟退火算法（SA），禁忌搜索算法(TS)，神经网络算法(GNN)，其中进化类算法包括遗传算法(GA)，差分进化算法(DE)，免疫算法（IA）等，其中群智能算法主要有粒子群算法（PSO），蚁群算法（ACO）等等

下面来逐一讲述

• 遗传算法（GA） 

• 遗传算法是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法。其特点高效，实用，鲁棒性强等特点。能有效的求解NP问题以及非线性、多峰函数优化和多目标优化问题。

多的不说，来讲主要内容吧

1.主要思想

   遗传算法是受生物进化过程中“优胜劣汰”的自然选择机制和遗传信息传递规律的启发，所提出的一种智能优化算法。遗传算法通过初始化种群、复制操作、交叉操作、变异操作几个步骤，模拟自然界生物进化过程中的繁殖行为与竞争行为，衍生出下一代的个体，再根据适应度的大小进行个体的优胜劣汰，提高新一代群体的质量，在经过反复多次迭代，逐步逼近复杂工程技术问题的最优解。

2.主要步骤

（1）初始化种群的产生（编码）

常见的编码方式有：

1、二进制编码

基因用0或1表示（常用于解决01背包问题）   

                

2、格雷码编码

连续的两个整数所对应的编码之间仅仅只有一个码位是不同的，其余码位都相同。

3、实数(浮点数)编码

个体的每个基因值用某一范围内的某个浮点数来表示，个体的编码长度等于其决策变量的位数，只能用于连续变量问题。

5、互换编码

用于解决排序问题，如旅行商问题和调度问题。

如旅行商问题中，一串基因编码用来表示遍历的城市顺序，如：234517986，表示九个城市中，先经过城市2，再经过城市3，依此类推。

（2）适应度函数的确定

遗传算法对一个个体（解）的好坏用适应度函数值来评价，适应度函数选择的越好，解的质量越高。常见构造方法为：目标函数映射成适应度函数，基于序的适应度函数等。

（3）遗传操作（选择，交叉，变异）

*选择操作：

遗传算法使用选择运算来实现对群体中的个体进行优胜劣汰操作：适应度高的个体被遗传到下一代群体中的概率大；适应度低的个体，被遗传到下一代群体中的概率小。选择操作的任务就是按某种方法从父代群体中选取一些个体，遗传到下一代群体。

常见的选择操作有：

1、轮盘赌选择（Roulette Wheel Selection）：

又称比例选择方法．其基本思想是：各个个体被选中的概率与其适应度大小成正比．

具体操作如下：
(1)计算出群体中每个个体的适应度f(i=1，2，…，M)，M为群体大小；
(2)计算出每个个体被遗传到下一代群体中的概率；

 

(3)计算出每个个体的累积概率；

  （q[i]称为染色体x[i] (i=1, 2, …, n)的积累概率）

 

(4)在[0，1]区间内产生一个均匀分布的伪随机数r；
(5)若r  

(6)重复(4)、(5)共M次

2、随机联赛选择（锦标赛选择）：

每次选取几个个体中适应度最高的一个个体遗传到下一代群体中。

*交叉操作：

所谓交叉运算，是指对两个相互配对的染色体依据交叉概率按某种方式相互交换其部分基因，从而形成两个新的个体。交叉运算在GA中起关键作用，是产生新个体的主要方法。

常见的交叉操作：

1、单点交叉：

指在个体编码串中只随机设置一个交叉点，然后在该点相互交换两个配对个体的部分染色体。

2、两点交叉与多点交叉：

（1）两点交叉：在个体编码串中随机设置了两个交叉点，然后再进行部分基因交换。

（2）多点交叉

3、均匀交叉（也称一致交叉）：

两个配对个体的每个基因座上的基因都以相同的交叉概率进行交换，从而形成两个新个体。

4、算术交叉：

由两个个体的线性组合而产生出两个新的个体。该操作对象一般是由浮点数编码表示的个体。例如：第k个基因w_k和第l个基因w_l在j位的交叉操作分别为：

w_kj=w_kj (1-b)+w_lj b,

w_lj=w_lj (1-b)+w_kj b

其中b为[0,1]间的随机数.

5、基于“ 与/或 ”交叉法 （用于二进制编码）

对父代按位"与”逻辑运算产生一子代A;按位”或”逻辑运算产生另一子代B。该交叉策略在解背包问题中效果较好。

如：交叉前：

01001011

11011101

交叉后：

01001001

11011111

6、部分匹配交叉（PMX）法（用于互换编码）

（常用于TSP）

先随机产生两个交叉点，定义这两点间的区域为匹配区域，并用交换两个父代的匹配区域。

父代A：872 | 130 | 9546

父代B：983 | 567 | 1420    变为：

TEMP A: 872 | 567 | 9546

TEMP B: 983 | 130 | 1420

对于 TEMP A、TEMP Ｂ中匹配区域以外出现的数码重复，要依据匹配区域内的位置逐一进行替换。匹配关系：1<——>５　３<——>６　７<——>０

子代Ａ：802 | 567 | 9143

子代Ｂ：986 | 130 | 5427

7、顺序交叉法(OX) （用于互换编码）

从父代Ａ随机选一个编码子串，放到子代Ａ的对应位置；子代Ａ空余的位置从父代Ｂ中按Ｂ的顺序选取（与己有编码不重复）。同理可得子代Ｂ。

父代A: 872 | 139 | 0546

父代B: 983 | 567 | 1420

交叉后：

子代A: 856 | 139 | 7420

子代B: 821 | 567 | 3904

*变异操作：

变异是指依据变异概率将个体编码串中的某些基因值用其它基因值来替换，从而形成一个新的个体。GA中的变异运算是产生新个体的辅助方法，它决定了GA的局部搜索能力，同时保持种群的多样性。交叉运算和变异运算的相互配合，共同完成对搜索空间的全局搜索和局部搜索。

注：变异概率Pm不能太小，这样降低全局搜索能力；也不能太大，Pm > 0.5，这时GA退化为随机搜索。变异概率,一般取为0.001~0.1

常见的变异操作：

1、基本位变异：（二进制编码）

对个体编码串中以变异概率、随机指定的某一位或某几位基因做变异运算。对于基本遗传算法中用二进制编码符号串所表示的个体，若需要进行变异操作的某一基因座上的原有基因值为0，则变异操作将其变为1；反之，若原有基因值为1，则变异操作将其变为0。

2、逆转变异算子（常用于TSP问题）

在个体中随机挑选两个逆转点，再将两个逆转点间的基因交换。

如：变异前：

1346798205

变异后：

1246798305

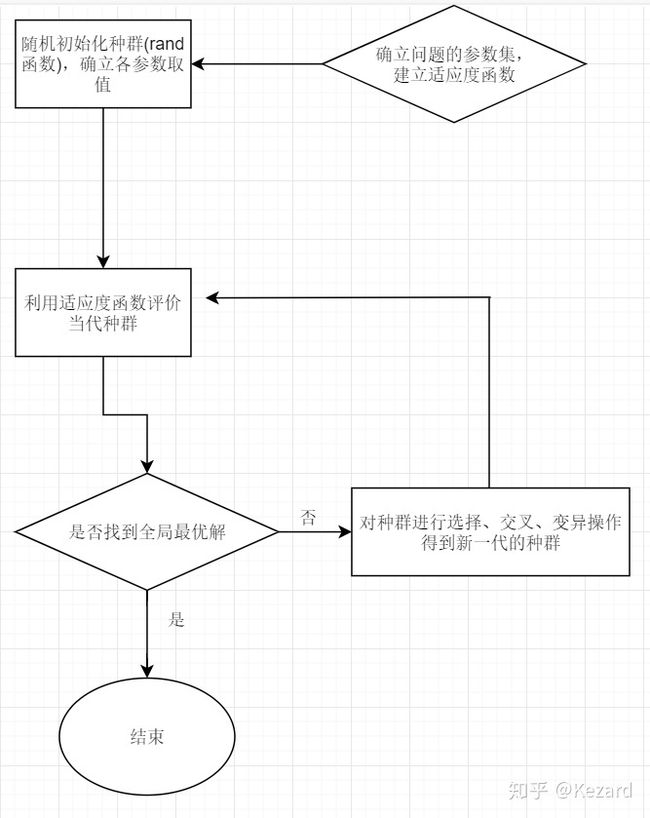
*算法流程图

 

 例题及源代码：

用标准遗传算法求函数f(x)=x+10sin(5x)+7cos(4x)的最大值，其中x的取值范围为[0,10].只是一个有多个局部极值的函数

%%%%%%%%%%%%初始化参数%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;
close all;
clc;
NP = 50;
L = 20;
Pc = 0.8;
Pm = 0.1;
G = 100;
Xs = 10;
Xx = 0;
f = randi([0,1],NP,L);
%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%%%%%%%%%%%%%
for k = 1:G
  %%%%%%%%%%%%将二进制解码为定义域范围内十进制%%%%%%%%%%%%
    for i = 1:NP
        U = f(i,:);
        m = 0;
        for j = 1:L
            m= U(j) * 2 ^ (j-1) + m;
        end
        x(i)= Xx + m * (Xx-Xs) / (2 ^ L - 1);
        Fit(i) = func1(x(i));
    end
    maxFit = max(Fit);
    minFit = min(Fit);
    rr = find(Fit == maxFit);
    fBest = f(rr(1,1),:);
    xBest = x(rr(1,1));
    Fit = (Fit-minFit)/(maxFit- minFit);
    %%%%%%%%%%%基于轮盘赌的复制操作%%%%%%%%%%%%%%
    sum_Fit = sum(Fit);
    fitvalue = Fit./sum_Fit;
    fitvalue = cumsum(fitvalue);
    ms = sort(rand(NP,1));
    fiti = 1;
    newi = 1;
    while newi <= NP
        if (ms(newi)) < fitvalue(fiti)
            nf(newi,:) = f(fiti,:);
            newi = newi + 1;
        else
            fiti = fiti + 1;
        end
    end
    %%%%%%%%%%%%%%%%%%%基于概率的交叉操作%%%%%%%%%%%%%%%%%%%%%%%%
    for i = 1:2:NP
        p = rand;
        if p < Pc
            q = randi([0,1],1,L);
            for j = 1:L
                if q(j)==1
                    temp = nf(i+1,j);
                    nf(i,j)= temp;
                end
            end
        end
    end
    %%%%%%%%%%%%%基于概率的变异操作%%%%%%%%%%%%%%%%%%%%%
    i = 1;
    while i <= round(NP * Pm)
        h = randi([1,NP],1,1);
        for j = 1 :round(L*Pm)
            g = randi([1,L],1,1);
            nf(h,g) = ~nf(h,g);
        end
        i = i+1;
    end
    f = nf;
    f(1,:) = fBest;
    trace(k) = maxFit;
end
xBest;
figure 
plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
%%%%%%%%%%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%%%%%%%%%
function result = func1(x)
fit = x + 10 .* sin(5 * x) + 7 .* cos(4 * x);
result = fit;
end