七, Java实现八大排序算法, 带源码详解
文章目录
-
- 前置知识:
- 一,选择类排序(简单选择和堆排序)
-
- 1,简单选择
-
- 基本思想:
- 实现思路:
- 稳定性: `不稳定`
- 原理演示:
- 代码实例:
- 2,堆排序
- 二, 插入类排序(直接插入和希尔排序)
-
- 3,直接插入排序
-
- 基本思想:
- 实现思路:
- 稳定性: `稳定`
- 原理演示:
- 代码实例:
- 4.希尔排序
-
- 前置知识:
- 稳定性: `不稳定`
- 原理演示:
- 三, 交换类排序(冒泡和快排)
-
-
- 5,冒泡排序
-
- 基本思想:
- 实现思路:★
- 稳定性: `稳定`
- 原理演示:
- 代码实例:
- 5-1, 冒泡排序的优化,一
- 6, 快速排序 (需要补充快排的优化!!!!!)
-
- 基本思想:
- 稳定性: `不稳定`
- 原理演示:
- 代码实例:
- 6.1 用前后指针的方式实现快排
- 四,归并排序
- 7, 归并排序
-
- 基本思想:
- 稳定性: `稳定`
- 原理演示:
- 实现流程概述:
- 代码实例:
- 五, 非比较排序
- 8. 基数排序
-
前置知识:
时间复杂度的定义和计算:
-
一般情况下,
算法中的基本操作语句的重复执行次数是问题规模为n的某个函数, 用T(n)表示, 若有某个辅助函数f(n), 使得当n趋于无穷大时, T(n)/f(n)的极限值为不等于零的常数, 则称 f(n)是T(n)的同数量级函数, 记作 T(n)=O(f(n)), 我们称O(f(n))为算法的渐进时间复杂度, 简称时间复杂度. -
计算时间复杂度的方法:
基本排序算法的种类
-
内部排序:待排序记录存放
在计算机内存中进行的排序过程。通过比较次数(时间复杂度)来衡量效率; -
外部排序:待排序记录的数量很大,以致于内存不能一次容纳全部记录,所以
在排序过程中需要对外存进行访问的排序过程。通过IO次数(即读写外存的次数)来衡量效率。 -
比较类排序:
通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。 -
非比较类排序:
不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,需要开辟额外的存储空间,因此也称为线性时间非比较类排序。
一,选择类排序(简单选择和堆排序)
1,简单选择
基本思想:
从无序数组中选出最小(或最大)的一个元素,存放在序列的起始位置(构成了有序数组),直到全部待排元素有序。
实现思路:
- 外层循环控制有序队列的最后一个元素,这个元素是动态变化的(从0—>len-1), min=i
- 而内层循环就是把这个元素与无序队列的所有元素一一比较, ?num[min] > num[j], 从而找出最小的元素的索引 min=j, 然后在内循环外,我们进行交换.
注意: 选择排序的时间比冒泡要快很多.
稳定性: 不稳定
如:5️⃣, 8,5, 2, 9
在第一遍排序中,2会与第一个5️⃣交换而放在第一列,此时第一个5️⃣会放在第二个5之后,此时两个5的相对次序会被破坏,所以简单选择是不稳定的排序。
原理演示:
代码实例:
//升序排列
package SortingAlgorithm;
class SelectSorting{
public void selectSorting() {
int min,tmp;
int []num= {
9,3,4,2,6,7,5,1};
//外层循环是从下标0开始对无序数组的遍历
for(int i=0; i<num.length-1; i++){
//设置最小值标志min,每循环一次都用i初始化,即min刚开始的位置始终是无序数列的第一个
min= i;
//内层循环是把无序数组的每个数与num[min]比较,遇到比他小的,则设置新的最小值标志(min = j)
for(int j=i+1; j<num.length; j++) {
if(num[j] < num[min])
min = j;
}
//min不等于i时说明最小值标志发生了变化,并且上面内循环的结束标志着对无序数组的一次遍历已经完成
//,我们可以知道此时的最小值num[min],理应与num[i]进行交换以放入到已经排好序的数列的末尾。
if(min!=i) {
tmp = num[i];
num[i] = num[min];
num[min] = tmp;
}
}
///打印排序后的数组
for(int k=0; k<8; k++)
System.out.print(num[k]+",");
}
///主函数
public static void main(String[] args) {
SelectSorting iS = new SelectSorting();
iS.selectSorting();
}
}
2,堆排序
十-4, 堆排序及其Java实现
二, 插入类排序(直接插入和希尔排序)
3,直接插入排序
基本思想:
将后面无序的一个元素与前面有序的队列中的元素一一进行比较,找到合适的位置之后将这个无序元素插入,插入后前面序列依旧有序(后无序插前有序)
实现思路:
- 外层循环遍历无序队列(i从1–>len-1),
- 内层循环(j从i-1到0 )倒序遍历无序前面的有序队列, 并不断跟无序队列的第一个元素比较, 直到找到这个元素应该的插入位置
稳定性: 稳定
原理演示:
举个栗子:
红框内为有序数列,红框后为无序数列(待排数列)
代码实例:
///主方法 //升序排列
package SortingAlgorithm;
class InsertSorting{
public void insertSorting() {
int tmp,j;
int []num= {
9,3,4,2,6,7,5,1};
//外循环负责对整个无序数组(从1到n.length)的遍历
//第一次排序就应拿第二个元素与第一个元素比较,所以无序数列的遍历应该从i=1开始,i=0只会让循环白白浪费一次。
for(int i=1; i<num.length; i++){
//把无序数组的第一个元素存在tmp中
tmp = num[i];
//有序数组的最后一个数的下标
j=i-1;
//遍历有序数组,并把tmp与有序数组中的每个元素进行比较,把大于tmp的数后移
while(j>=0 && num[j]> tmp){
num[j+1]=num[j];//数组后移,把无序数组arr[i]覆盖掉了,但是没关系我们保存到tmp了
j--;
}
//找到小于tmp的数之后,把tmp插入到这个数的后面
num[j+1]=tmp;
}
///--------打印排序后的数组
for(int k=0; k<8; k++)
System.out.print(num[k]+",");
}
//---------主函数
public static void main(String[] args) {
InsertSorting iS = new InsertSorting();
iS.insertSorting();
}
}
4.希尔排序
前置知识:
希尔排序又称为缩小增量排序,是插入排序的改进版
Java实现希尔排序的两种方法(交换法和移位法), 看了还不会手撕代码来打我!
稳定性: 不稳定
由于多次插入排序,在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱
原理演示:
三, 交换类排序(冒泡和快排)
5,冒泡排序
基本思想:
从头到尾,重复走访要排序的序列,一次比较两个元素,如果排列方式错误就把他们交换过来,直到没有需要交换的元素。
实现思路:★
- 外层循环控制比较趟数, 内层循环控制每趟比较的比较次数.
- 冒泡排序: 两两比较, 所以N个元素比较趟数是 N-1趟(外层循环的职责, i 从0–>n-1, 比较发生了n-1趟); 每一趟比较必然会使一个元素到达最终位置, 所以每一趟的比较次数为 N-i-1(i记录了当前趟数,i趟就有i个 元素已经排好序,所以未排好序的还有n-i个元素, 这n-i个元素需要比较n-i-1次)(此为内层循环的职责, j从 0–> n-i-1);
稳定性: 稳定
因为在比较的过程中,当两个相同大小的元素相邻,只比较大或者小,所以相等的时候是不会交换位置的。而当两个相等元素离着比较远的时候,也只是会把他们交换到相邻的位置。他们的位置前后关系不会发生任何变化,所以算法是稳定的
原理演示:
在最好情况下如果数列已经有序,那么我们只需一趟便可使数列完成排序,这一趟中排序次数为n-1次,所以此时复杂度0(n)。在最坏情况下,数列仍未有序我们还需n-1趟,每趟需要比较n-1-i次,此时的复杂度为0(n2);
代码实例:
package SortingAlgorithm;
class BubbleSorting{
public void bubbleSorting() {
int min,tmp;
int []num= {
9,3,4,2,6,7,5,1};
//每排序一次,至少一个元素有序,所以i趟排序就会有i个元素有序,进而得出第i趟未被排序的元素还有N-i个
//N个数字要排序完成,总共进行N-1趟排序,故每i趟的排序次数为(N-i-1)次
//外层控制循环多少趟,内层控制每一趟的比较次数
for(int i=0; i<num.length-1; i++){
for(int j=0; j <num.length-i-1;j++) {
if(num[j]>num[j+1]) {
tmp = num[j];
num[j] = num[j+1];
num[j+1] = tmp;
}
}
}
//-----打印排序后的数组
for(int k=0; k<8; k++)
System.out.print(num[k]+",");
}
/主函数
public static void main(String[] args) {
BubbleSorting iS = new BubbleSorting();
iS.bubbleSorting();
}
}
5-1, 冒泡排序的优化,一
如果我们发现在冒泡排序的
某一趟比较时, 一次数据的交换也没有发生, 那这个待排序列其实已经有序了,没有必要再继续循环了,可以直接跳出循环了. 通过这个原理,我们可以对冒泡排序进行优化(通过设置flag来实现)
代码如下:
package DataStrcture.SortAlgorithmsDemo;
import java.util.Arrays;
public class UpdateBubbleSortDemo {
/**
* 如果在某一趟排序时,未发生任何的数据交换, 那么这个待排队列就是有序的了,我们直接跳出循环就可以了
* 依此原理,我们对排序过程进行优化.
*/
public static void main(String[] args) {
int temp;
int arr[] = {
3,9,-1,10,20};
//外层循环控制比较的趟数, 内层循环控制每趟比较的次数
for(int i=0; i<arr.length; i++){
boolean flag = false;//是否比较了
for( int j=0; j<arr.length-i-1; j++){
if(arr[j] > arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
flag = true;
}
}
System.out.println("进行了第"+(i+1)+"趟");
//把数组转为字符串输出
System.out.println(Arrays.toString(arr));
//如果有一趟排序未发生队列数据的交换,则跳出冒泡的这俩循环;
if(!flag){
break;
}
}
}
}
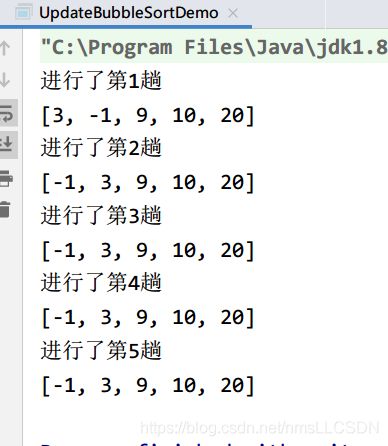
优化后的执行结果:
未优化的冒泡排序趟数:
6, 快速排序 (需要补充快排的优化!!!)
基本思想:
快排是对冒泡的一种改进,其原理是将要排序的数据分割成独立的两部分,其中一部分的所有数据都要比另一部分的所有数据小,然后按此方法对这两部分分别进行快速排序。整个过程可递归进行,以此让数据有序。
稳定性: 不稳定
多个相同值的相对位置可能会在算法结束时发生变动
原理演示:
代码实例:
package SortingAlgorithm;
class QuickSorting{
///本段快排的基本原理:
//把begin看做快排中比较基准值的下标.(begin是待排序列数组的第一个数的下标,相应的,end代表待排序列的最后一个数的下标.)
//根据快排的思想,我们需要根据基准值num[begin]把数组中的待排数列划分为两段序列,左段的序列都比num[begin]小,右段的都比num[begin]大.
//我们用i做左段序列数组的下标,用j做右段序列数组的下标.在i
public void quickSorting(int num[], int begin, int end) {
int i = 0,j = 0;
///begin < end的时候不断执行下面的比较交换操作
//?什么时候停止? 每一小段的数都有序.
if(begin >= end) {
return; //递归结束的条件/出口
}
//标记前一段比较序列开头下标,后一段比较序列的末尾下标
i = begin+1;
j = end;
当前段序列下标小于后段序列下标的时候,不断把前段的数与基准值num[begin]比较,
//把比基准值大的num[i]与num[j]交换,此时后段序列下标应向前移动一位(j--).
//相反,若num[i]比num[begin]小,则说明这个num[i]处于正确的段内,只需向后继续比较(i++);
while(i<j) {
if(num[i] > num[begin]) {
swapArray(num, i, j);
j--;
}else {
i++;
}
}
/前后两段比较完成后, 此时i=j
//接下来确定num[begin]的位置
//只需比较num[bein]和num[i],交换num[begin]和num[i]的位置
if(num[i] > num[begin]) {
i--;
}
swapArray(num, i, begin);
quickSorting(num, begin, j-1);
quickSorting(num, j, end);
}
交换同一数组中两个数的方法
public void swapArray(int[] number, int index1, int index2) {
int tmp;
tmp = number[index1];
number[index1] = number[index2];
number[index2] = tmp;
}
public static void main(String[] args) {
int[] num = {
9,3,4,2,6,7,5,1};
int begin = 0;
int end = num.length-1;
QuickSorting iS = new QuickSorting();
iS.quickSorting(num,begin,end);
//直接使用Arrays 的toString(arr)方法输出数组
System.out.println("快排后的结果为: "+ Arrays.toString(num));
}
在写快排的程序时,要时刻注意数组下标的写法,防止数组越界
另外,书写swap方法时,要注意交换两个数字和交换两个数组中数字的写法上的差异!!!
数组是引用数据类型, 所以我们在交换数组中两个数时,需要把数组以及需要交换的两个索引作为方法的形参传入;
6.1 用前后指针的方式实现快排
package DataStrcture.SortReview531;
import static DataStrcture.SortAlgorithmsDemo.QuickSortRW530.swapArr;
public class QuickSortNew607 {
//前后指针实现快排
/**
* cur指示当前的遍历位置, pre指向cur 的前面位置
* 注意: 在前后指针法中, 前指针pre前面的值比基准值都要小, 前指针pre到后指针cur之间的值都要比基准值大
* 在 cur < right情况下, 不断比较 cur和right对应的值,
* 1. arr[cur] >= arr[right], cur指针后移, pre指针不动
* 2. arr[cur] < arr[right], pre指针先后移,交换cur和pre对应的值, cur再后移
* 3. 本趟排序之后, 把基准值arr[right]与 pre+1 进行交换
*/
public static void quickSort(int[] arr, int left, int right){
if(left >= right) return;
int pre = left - 1;
int cur = left;
while(cur < right){
if(arr[cur] < arr[right]){
pre++;
swapArr(arr, cur, pre);
cur++;
}else{
cur++;
}
}
pre++;
swapArr(arr, pre, right);
///?????????
quickSort(arr, left, pre-1);
quickSort(arr, pre+1, right);
}
public static void main(String[] args) {
// int arr[] = {8, 23, 5, 1, 6, 3, 2, 1, 7};
int arr[] = {
49, 38, 65, 97, 76, 13, 27, 49};
quickSort(arr, 0, arr.length-1);
for(int x : arr){
System.out.print(x + ", ");
}
}
}
四,归并排序
7, 归并排序
基本思想:
归并排序算法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
稳定性: 稳定
原理演示:
实现流程概述:
- 根据上面的动图, 我们很容易知道归并排序就是分治法的一个典型,
- 最先开始的是分, 先通过递归把待排序列不断的往下细分, 直到分成了一个个独立的数,
- 然后我们在使用比较同时进行合并, 把一个元素和另一个元素按升序或逆序的顺序合并为两个元素, 三个, 四个…直到达到待排序列的长度;
[具体的实现流程]
- 对于归并排序, 我们通过使用递归对待排序列进行不断地往下细分, 直到每个子问题是一个单独的值
- 然后在递归进行返回的时候, 递归是如何返回的呢? 先是两个数,再是三个数, 直到返回整个待排序列, 在返回的同时我们需要对每次返回的数进行排序, 如何排序呢? 通过比较mid两边的值, 合适的值会被临时数组等待此单次排序完成后放入原数组;
代码实例:
package DataStrcture.SortAlgorithmsDemo;
public class MergeSortRW530 {
//归并排序, 先分后合并排序
//1. 先分然后调用排序方法进行排序
public static void mergeSort(int[] arr, int begin, int end) {
if (begin >= end) return;
int mid = (begin + end) / 2;
mergeSort(arr, begin, mid);
mergeSort(arr, mid + 1, end);
sort(arr, begin, mid, end);
}
// 2. 对数组中的两部分进行比较以重新排序
public static void sort(int[] arr, int begin, int mid, int end) {
//定义临时数据temp, 临时存放排序了的数
int[] temp = new int[arr.length];
int beginIndex = begin;
int endIndex = mid + 1;
int tempIndex = 0;
//比较双方都还有待比较的数
while (beginIndex <= mid && endIndex <= end) {
if (arr[beginIndex] < arr[endIndex]) {
temp[tempIndex] = arr[beginIndex];
tempIndex++;
beginIndex++;
} else {
temp[tempIndex] = arr[endIndex];
tempIndex++;
endIndex++;
}
}
//比较双方一方遍历完成, 还有一方还剩一些数
while (beginIndex <= mid) {
temp[tempIndex++] = arr[beginIndex++];
}
while (endIndex <= end) {
temp[tempIndex++] = arr[endIndex++];
}
//把临时数组赋值给原数组
for (int i = 0; i < tempIndex; i++) {
arr[i+left] = temp[i];
}
}
//测试方法
public static void main(String[] args) {
int[] a = {
49, 38, 65, 97, 76, 13, 27, 50};
mergeSort(a, 0, a.length - 1);
System.out.println("排好序的数组:");
for (int e : a)
System.out.print(e + " ");
}
}
待补充: 掌握需要加强,补充更多侧面知识点, 对个别算法继续优化的学习.时间复杂度的掌握
五, 非比较排序
8. 基数排序
参考资料:
https://blog.csdn.net/qq_36427244/article/details/95593452