【SLAM学习笔记4】卡方检验chi-square
文章目录
- 前言
- 一、卡方分布
- 二、卡方检验
-
- 计算步骤
- 关于自由度n
- 查表
-
- 检验统计量拒绝域内外判定:
- 决策原则
- 总结
- Reference
前言
卡方分布和卡方检验在很多地方都会用到,尤其是统计学和数据分析里。
卡方检验(chi-square,记为χ2检验)是一种计数资料的假设检验方法,因为对总体的分布不作任何假设,故属于非参数检验。
第一次碰见是在ORB-SLAM2检验单应矩阵中。
现在在卡方检验重新梳理一下。
一、卡方分布
卡方检验是基于卡方分布的一种假设检验方法。
实际观察次数fo与理论(期望)次数fe之差的平方除以理论次数fe所得的值,近似服从卡方分布。
卡方检验的公式:
卡方分布的定义与性质:


E(X):期望值;Var(X):方差。
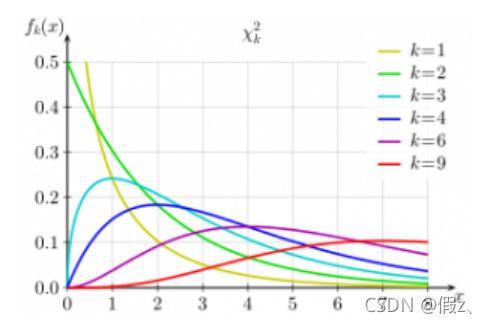
通常,Xn2密度函数的定义域为(0,+∞),且自由度n越大,其密度曲线越趋近于对称;n越小,曲线越不对称。
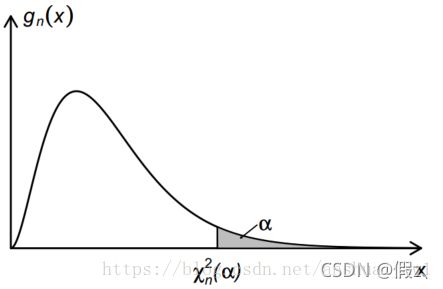
若X ~ Xn2,记 P (x>c) = α, 则 c = Xn2(α) 则称为Xn2分布的上侧α分位数,如下图所示,gn(x)是Xn2的密度函数。
注:显著性水平是:估计总体参数落在某一区间内,可能犯错误的概率,用α表示。
当α和n给定时,可查表得到 Xn2(α)的值。如 X102(0.01) = 23.209, X52(0.05) = 12.592等。
二、卡方检验
卡方检验(chi-square,记为χ2检验)是一种计数资料的假设检验方法,因为对总体的分布不作任何假设,故属于非参数检验。
根本思想:比较实际频次fo与理论频次fe的吻合程度或拟合优化问题
使用的情况:当事实与期望不符合情况下使用卡方分布进行检验,看是否系统出了问题,还是属于正常波动。利用卡方分布分析结果,排除可疑结果。
作用:主要用于比较两个及两个以上的样本率或分类变量的关联性分析。检查实际结果与期望结果之间何时存在显著差异。
- 检验拟合程度:可以检验一组给定数据与指定分布的吻合程度。如:检验抽奖机收益的观察频数与我们所期望的吻合程度。
- 检验两个变量的独立性:通过这个方法,检查变量之间是否存在某种关系。
步骤:
- 确定要进行检验的假设H0,及其备择假设H1.
- 求出期望E.
- 确定用于做决策的拒绝域(右尾).
- 根据自由度和显著性水平查询检验统计量临界值.
- 查看检验统计量是否在拒绝域内.
- 做出决策.
显著性水平是:估计总体参数落在某一区间内,可能犯错误的概率,用α表示。
显著性水平是假设检验中的一个概念,是指当原假设为正确时人们却把它拒绝了的概率或风险。它是公认的小概率事件的概率值,必须在每一次统计检验之前确定,通常取α=0.05或α=0.01。这表明,当作出接受原假设的决定时,其正确的可能性(概率)为95%或99%。
检测标准:卡方分布检验是单尾检验且是右尾,右尾被作为拒绝域。于是通过查看检验统计量是否位于右尾的拒绝域以内,来判定期望分布得出结果的可能性。
计算步骤
期望频数总和与观察频数总和相等
- 表里填写相应的观察频数和期望频数
期望频数 = 观察频数总和*出现某种结果的概率,其实就是求期望值。
如下表的,X= -2的期待频数为977。

- 利用卡方公式计算检验统计量

检验统计量X2意义:fo与fe之间差值越小,检验统计量X2越小。
卡方检验的标准:如果统计量值X2很小,说明实际观察频数和期望频数之间的差别不显著;统计量越大,差别越显著。故还是越小越好。
按观察频率和期望频率表(上表),计算检验统计量X2:
关于自由度n
自由度:用于计算检验统计量的独立变量的数目。
- 当自由度等于1或者2时:卡方分布先高后低的平滑曲线,检验统计量等于较小值的概率远远大于较大值
的概率,即观察频数有可能接近期望频数。 - 当自由度大于2时:卡方分布先低后高再低,其外形沿着正向扭曲,但当自由度很大时,图形接近正态分
布。
自由度的计算:
对于单行或单列:自由度 = 组数 - 限制数
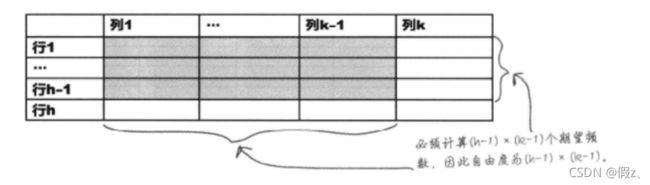
对于表格类:自由度 = (行数 - 1) * (列数 - 1)
查表
检验统计量拒绝域内外判定:
- 求出检验统计量a
- 通过自由度和显著性水平查到拒绝域临界值b
- a>b则位于拒绝域内;反之,位于拒绝域外。
例子:
假设自由度为4, 5%的显著水平,查表得到其拒绝域是9.49,也就是说检验统计量大于9.49位于拒绝域内。
按上面计算得到的检验统计量X2 = 38.272 > 9.49 位于拒绝域内。
决策原则
如果位于拒绝域内我们拒绝原假设H0,接受H1。
如果不在拒绝域内我们接受原假设H0,拒绝H1。
上述,因为检验统计量38.272 > 9.49 位于拒绝域内,所以拒绝原假设,接受备择假设。
比如,
原假设H0是:机器没有故障,一切正常
备择假设H1:机器故障,违反常规。
总结
本文为了ORB-SLAM2中的一些卡方检测(例如,剔除外点策略)而准备。
Reference
- https://blog.csdn.net/jinxiaonian11/article/details/78617936(卡方分布分析与应用)
- https://blog.csdn.net/anshuai_aw1/article/details/82735201(三大抽样分布:卡方分布,t分布和F分布的简单理解)【重点】
- @计算机视觉life课程(yyds)