Python 用推导式解决“七段码”问题

 源代码

from itertools import chain,combinations as comb

if __name__ == '__main__':

    L = list('abcdefg')
    C = [[''.join(c) for c in list(comb(L,i+1)) if 'g' in c] for i in range(7)]
    D = list(chain.from_iterable(C))
    X = [e for e in D if 'a' in e and 'b' not in e and 'f' not in e 
                        or 'd' in e and 'c' not in e and 'e' not in e]
    E = [d for d in D if d not in X]

    L = list('abcdef')*2
    A = [L[i:j] for i in range(len(L)) for j in range(i+1,len(L)+1) if len(L[i:j])<7]
    B = list(set([''.join(sorted(a)) for a in A]))

    F = sorted(B + E)
    print('可表达字符总数：',len(F))
    print('所有组合的列表：',F)

运行结果

可表达字符总数： 80
所有组合的列表： ['a', 'ab', 'abc', 'abcd', 'abcde', 'abcdef', 'abcdefg', 'abcdeg', 'abcdf', 'abcdfg', 'abcdg', 'abcef', 'abcefg', 'abceg', 'abcf', 'abcfg', 'abcg', 'abdef', 'abdefg', 'abdeg', 'abef', 'abefg', 'abeg', 'abf', 'abfg', 'abg', 'acdef', 'acdefg', 'acdfg', 'acefg', 'acfg', 'adef', 'adefg', 'aef', 'aefg', 'af', 'afg', 'b', 'bc', 'bcd', 'bcde', 'bcdef', 'bcdefg', 'bcdeg', 'bcdfg', 'bcdg', 'bcefg', 'bceg', 'bcfg', 'bcg', 'bdefg', 'bdeg', 'befg', 'beg', 'bfg', 'bg', 'c', 'cd', 'cde', 'cdef', 'cdefg', 'cdeg', 'cdfg', 'cdg', 'cefg', 'ceg', 'cfg', 'cg', 'd', 'de', 'def', 'defg', 'deg', 'e', 'ef', 'efg', 'eg', 'f', 'fg', 'g']

解题思路

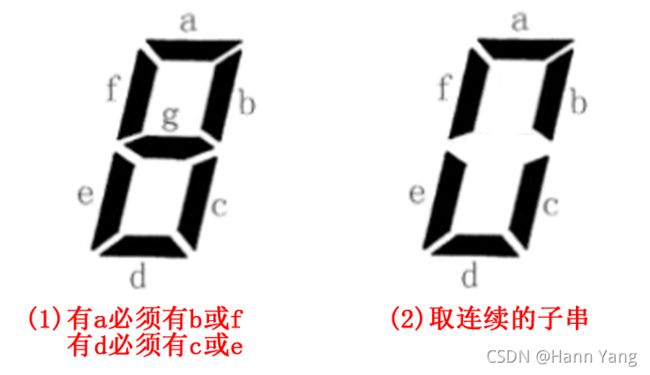
分两类进行分别计算：第一类是g段处于点亮状态，即在'abcdefg'中取出所有字母组合，但要排除不包含g的，排除后有64种；最后还要排除含a但不含b或f的、含d但不含c或e的共15个（“有了a但没有b或f就形成ag不连通”，另一个同理），排除后共49种组合。
第二类是g段不点亮状态即不包含g段，可以看作a~f组成的是一个环（零），所以需要在双倍长度的字符串'abcdefabcdef'中取出所有长度为1~6的所有子串，共有57种；每个字串内部作排序后再去重，留下31种组合。这样，两类总共合计有80种组合。

欢迎加入CSDN社区！https://bbs.csdn.net/forums/PythonTogether