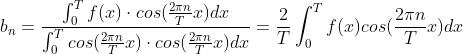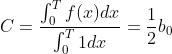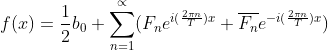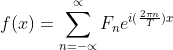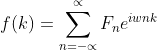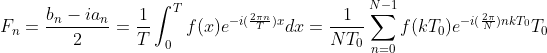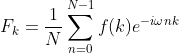傅里叶级数和傅里叶变换详细推导及其在python的应用

最近，应研究室需要，在导师慈善的注视下，作为新生的我勤勤恳恳地开始啃傅里叶变换相关知识，又是看书又是找各种博客，昨日刚完成了导师的一个小任务，着实觉得学习历程之辛苦，最主要还是知识点的散乱和驳杂，因此在此做一个小总结，希望能对后来者有点帮助。如果能得到各位老爷们的赞，实属荣幸。

傅里叶变换，尤其是离散傅里叶变换以及其简化运算的快速傅里叶变换应用广泛，本文将详细地从连续傅里叶级数开始，推导离散傅里叶级数，连续傅里叶变换和离散傅里叶变换，顺便会用python做一个连续傅里叶级数的展开（曲线拟合），一个离散傅里叶变换实例和一个快速傅里叶变换实例（所有实例代码都会贴在文章最下面）。

参考材料为《信号与系统》（华中科技大学出版社出版）的第一，四，五章，加上众多大佬的博客（之后会一一列出），最后加上一点自己的理解。不会涉及快速傅里叶变换（FFT）的知识，毕竟FFT只是DFT的简化运算，想看的伙伴可以去看看《数字信号处理（第2版）》（中国工信出版集团）的第七章“快速傅里叶变换（FFT）”。

废话不多说，正式开始。

连续傅里叶级数推导（CTFS）：

傅里叶认为任何周期函数都能用不同振幅，不同相位正弦波叠加而形成。

可能有的同学会不理解这句话的具体含义，确实有点抽象，这句话的具体理解待会儿会用图解具体说明，且按下不表，先把这句话当作一个数学定理即可。

根据这个“数学定理”，任意周期函数f(x)都能以正弦波叠加表示。而任何函数又都可以写为一个奇函数和一个偶函数之和。那么，周期为T的f(x)可以表示为不同振幅，不同相位正弦波之和：

这就是连续傅里叶级数展开，很简单对吧。

重点在于如何解C，an和bn这三个系数？

解的方法多种多样，在此我推荐函数正交基法，主要是原理容易理解且计算简单。

那么什么是函数正交基法呢？

先来看一个简单的例子，假设要你求一个向量A = ai+bj的系数a和b，你会怎么办？自然而然是用投影法：

A在i上的投影除以i的模长即为a：

同理A在j上的投影除以j的模长即为b。在此处，i和j就是一对正交基，而把这个方法拓展到函数领域，就成为了函数正交基法。

因为在上面的例子中要用到向量点乘，所以先拓展一下函数点乘的公式，假设求g（x）和m（x）两个函数的点乘，则：

好了，根据投影法的原理和函数点乘的公式，我们可以得到：

上面三个一大坨的式子，乍一看让人眼花缭乱，其实真的一点不难。有兴趣的小伙伴可以自己推导一下。

之后只要把三个系数带回方程即可得到f(x)的表达式了，这也就是连续傅里叶级数展开的三角函数表达式。但是，三角函数表达式太过于复杂，在计算机中应用比较麻烦，因此，神奇的欧拉公式便出场了，注意，欧拉公式在此处的作用仅仅是简化计算，如果不嫌麻烦，直接用三角函数表达式即可~~

欧拉公式推导非常简单，根据泰勒展开得来（想了解的小伙伴可以百度一下），这里就省略推导过程，直接上公式：

乍看非常简单，但欧拉公式的意义惊人，堪称伟大（自行百度）

从这个公式又能推导出另一种形式的欧拉公式：

把这俩式子变换一下带入到我们最初的f(x)中，得：

经化解得：

其中：

其共轭复数为：

观察发现，

再利用共轭复数的性质：

可以合并这个冗长的式子，变为：

这个式子就是指数形式的连续傅里叶级数展开，相比三角函数形式的傅里叶级数展开来说，这个式子在写程序的时候更方便。

连续傅里叶级数展开就是把一个周期函数分解为无穷个三角函数，那么它反过来是怎么样的呢？

自然是无穷个三角函数拟合为一个周期函数，这就是反连续傅里叶级数展开。

观察细致的伙伴可能已经发现了，Fn代表着an和bn的关系，也就是最开始式子的sin和cos的系数，那么这岂不意味着每一个Fn都决定了一个三角函数？也就是说每一个Fn都是那无穷个拟合f（x）的三角函数的一份子。

因此，反连续傅里叶级数展开：

连续傅里叶级数展开及其逆展开就是以上的内容了。连续傅里叶级数展开实际上分离出了无穷个三角函数，而其逆展开则用这无穷个三角函数逼近你所要的函数。连续傅里叶级数展开在频域上是离散且非周期的，如果仍然不太了解连续傅里叶级数和频域的基础知识，可以参考这个大佬的博客：(64条消息) 深入浅出的讲解傅里叶变换（真正的通俗易懂）_l494926429的博客-CSDN博客_傅里叶变换

讲得非常清楚明了，俺也是从这篇文章开始学习傅里叶相关知识。

如果觉得我在连续傅里叶级数讲的不清楚的童鞋，也可以去看看这位大佬的推导，他对正交基方法的讲解更详细明白：

(64条消息) 傅里叶变换推导_ShaYx1991的博客-CSDN博客_门函数傅里叶变换

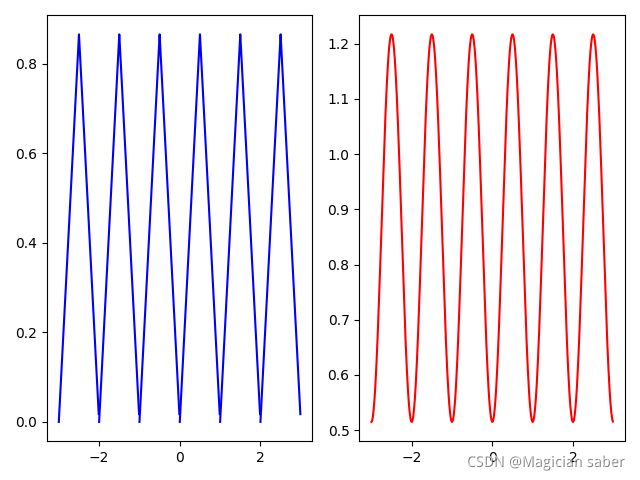
在这里先往回填一个坑，“任何周期函数都能用不同振幅，不同相位正弦波叠加而形成”，仍然不理解这句话的伙伴请看下面几幅图，这是我用python拟合的三角波，N表示拟合的阶数，也就是“用了多少条曲线合成”的意思。左侧是原波形图，右侧是拟合图：

N=2时：

N=8时：

 

 N=100时：

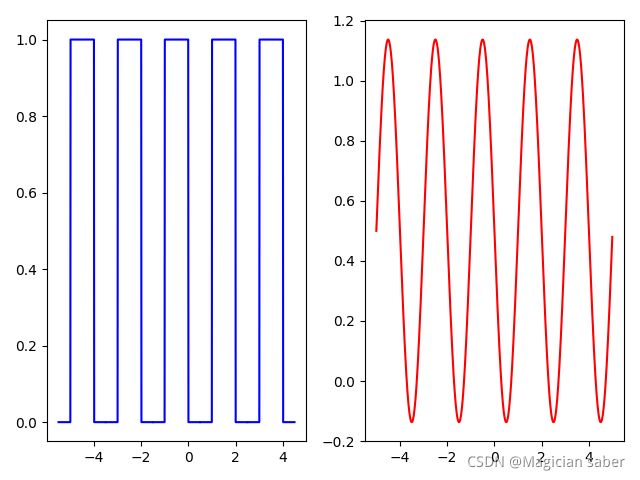
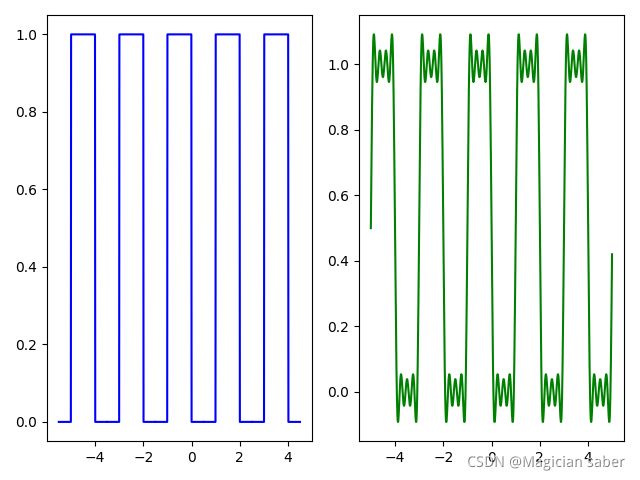
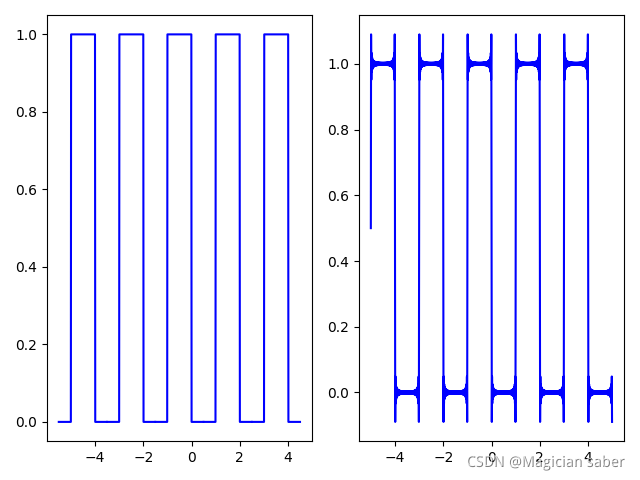
 可能三角波太简单，小伙伴们觉得也没啥差别，我做了一个矩形波，通过这个矩形波的拟合，应该就有点明白了。左侧是原波形图，右侧是拟合图：

N=2：

N=8：

 

N=100：

 

可以很明显看出，随着N的增大，拟合波形越来越接近原波形，这个过程，实质上就是"任何周期函数都能用不同振幅，不同相位正弦波叠加而形成"这句话的具象化解释。

连续傅里叶级数展开就到此为止，废话不多说，开始下一部分。

离散傅里叶级数推导（DFS）：

在频域上，不同于连续傅里叶级数展开得到的离散且非周期性的频谱图，离散傅里叶级数展开得到的频谱图是离散且周期性的。至于为什么是周期性的，容我之后解释，先从推导开始。从连续傅里叶级数展开，只需离散化，就能轻易得到离散傅里叶级数展开。

那么如何离散化呢？

很简单，既然是离散傅里叶级数展开，所给信号，也就是需要分解的函数，是离散的，直观地讲，是一个一个小点构成的非连续图像。如果把原函数的自变量x看作是时间t，那么离散化处理可以看作是在原连续图像上进行等时间采样。设采样周期为To（原函数f(x)的周期设为T），N为一个周期的采样数，w为数字频率。注意，我们先前推导的2pi*n/T中的2*pi/T是模拟角频率Ω，而在此处要转化为数字频率w，这是为了方便离散化。

综上有以下等式：

由此可以推出数字频率w为：

如果不理解以上模拟角频率w和数字频率Ω的关系的小伙伴，我推荐你可以看一下这个大佬的文章：深入浅出的讲解傅里叶变换（真正的通俗易懂）_l494926429的博客-CSDN博客_傅里叶变换

这大佬已经把三种频率的关系列的明明白白，模拟频率f在之后的离散傅里叶变换（DFT）也得要用到，因此早看早轻松啦~~

刚刚已经设定了采样周期和一个周期的采样数，那么可以进行时间上（也可理解为自变量x）的离散化，既然设定了采样周期，那么最小时间（即自变量）单位为To，t（即自变量x）也会化为离散的点kTo（k为整数），代入连续傅里叶级数，则可以完成离散化。

连续傅里叶级数的离散化：

因为是以To为一个单位时间，所以可以把To看作单位1，即略去To。

刚才有说，离散傅里叶级数展开得到的频谱图是离散且周期性的，那么周期性体现在哪呢？其实就蕴含在这个式子里（l代表正整数）：

因为n是整数，又因为我们之前设定f(x)的周期为T，所以上面的式子一定成立。

既然f(k)具有周期性，那么k不需要取到无穷，只需要从0取到N-1即可，而且n也不需要取到无穷，也只需要从0取到N-1即可，因此离散傅里叶级数展开为：

其中k=0，1，2，3，......，N-1

推导完离散傅里叶级数展开，再来看看反离散傅里叶级数展开，同样的道理，既然设定了采样周期，那么t（即自变量x）也会化为离散的点kTo（k为自然数），而作为最小时间（即自变量）单位的To可以看作dt，带入原式，完成离散化：

同理，把To看作单位1，并把w代入，反离散傅里叶级数展开为：

其中k=0，1，2，3，......，N-1

以上就是离散傅里叶级数的推导过程，虽然个人感觉没啥问题，但如果有小伙伴觉着有问题，记得留言，可以一起讨论呀。

废话不多说，下一个部分。

连续傅里叶变换推导（CTFT）：

傅里叶级数是把周期函数展开，那么如何把非周期函数展开呢？

大神们发明了一种把非周期函数伪装成周期函数的方法，那就是把非周期函数看成周期为无限大的周期函数，即T趋向于无穷。

在此基础上推导出的连续傅里叶级数就是连续傅里叶变换。

既然T趋近于无穷大，那么其频谱图的横轴的间隔，即模拟频率f（f=1/T）会趋近于无穷小，那么原本离散的频谱图就会转变为连续的频谱图。

因此必须引入频谱密度F，频谱密度F：

引入频谱密度的原因是模拟频率变成了无穷小，可以说变成了连续的变量，那么模拟频率变的连续了，模拟角频率和数字频率能逃得过么？

答案当然是不能！所以，在连续傅里叶级数中的模拟角频率也要变的连续(无穷小)，故nΩ=2*pi*n/T=Ω，且有等式：

将上述的两个式子代入连续傅里叶级数，得：

这就是连续傅里叶变换：

同理，反连续傅里叶变换也可以推导得到：

注意，这里的F并不是一个值

从连续傅里叶级数推导连续傅里叶变换还是比较简单得，有兴趣得小伙伴可以自己推导一下。

废话不多说，下一部分。

最后，也是最常用的离散傅里叶变换。

离散傅里叶变换：

离散傅里叶变换和离散傅里叶级数推导类似，但它要进行两次离散化，一次是时间轴上（即自变量）的离散化，还有一次是频率的离散化。但是离散傅里叶变换有点特殊，频谱图有两种形式，一种是离散，一种是连续。

在说这一点之前，我们先小结一下之前推导的频谱图。首先是周期函数的展开，当周期函数是连续时，用连续傅里叶级数展开，得到离散且非周期的频谱图，当周期函数时离散时，用离散傅里叶级数展开，得到离散且周期性的频谱图。非周期函数的展开，当非周期函数是连续时，用连续傅里叶变换，得到连续且非周期的频谱图。从此处可以看出时域和频域其实是对等的，这也衍生出广为人知的那两句：“周期对离散，离散对周期”，“非周期对连续，连续对非周期”。

那么由此推测，离散傅里叶变换得到的频谱图应该是连续且周期性的。

这当然是正确的，理论上，离散傅里叶变换得到的频谱图就应该是连续且周期性的。

注意，是理论上。

可能有小伙伴要问了，难道还有非理论情况？

这就跟你高中物理中说的理想条件，比如绝对光滑一样，实际中是不可能出现理想条件的。

我们之前说过的傅里叶级数和傅里叶变换，都是委托给计算机计算，包括采样也是由计算机进行，我们所做的一切都是为了计算方便。

在离散傅里叶变换时，我们面临一个问题，如何把非周期函数伪装成周期函数。有的伙伴可能会说，你就按照之前推导连续傅里叶变换一样，把它看成周期无限大的周期函数不就完了？

道理是这个道理，我们明白，大神们当然也明白，奈何计算机做不到啊。

周期无限大，计算机采样就需要采到无穷，而计算机只能采到有限的样本。因此，适用于连续傅里叶变换推导的“伪装周期法”并不完全适用离散傅里叶变换的推导。之所以说是不完全适用，那是因为本质道理还是一样的，我们依然要采取伪装，但这次得换换方式。

假设给了我们一段有限的离散非周期信号，我们可以直接把它当作周期信号，也就是说在时域上，无数次复制粘贴这一段有限的离散非周期信号，这种方法叫周期延拓，做出的离散傅里叶变换就是DFT。初闻此法，我差点蚌住了，这哪是什么伪装法，这不就假戏真做了吗？但想不到效果立竿见影，之后会用代码展示一下DFT。

另一种方法为补零法，即对信号以外的点做补零处理，补零法做出的离散傅里叶变换为DTFT。有兴趣的小伙伴可以自行搜索一下，在此就不详述了。

其实能很明显看出两种方法的差别，周期延拓是把信号转换成了周期信号，那么做出来的频谱图就是离散的，而补零法仍然维持信号的非周期性，做出的频谱图是连续的。这也是我说离散傅里叶变换特殊的原因。这两种方法简单直观的解释可以看看知乎这位大佬的：

如何理解傅里叶变换时域连续对应频域非周期，时域离散对应频域周期？ - renaissance的回答 - 知乎 https://www.zhihu.com/question/26448935/answer/1189713815

我们来详细说一说DFT的推导。 

与离散傅里叶级数推导类似，我们只需要把连续傅里叶变换离散化，就能得到离散傅里叶变换。与离散傅里叶级数推导类似，我们可以把模拟角频率Ω转换为数字频率w：

在此前的离散傅里叶级数推导中，我们将时间离散化，在这里也是一样的，dt转化为To，t转化为kTo（k为整数），在此前的连续傅里叶变换推导中，我们把数字频率和模拟角频率连续化了，在此刚好相反，需要将其离散化，w转化为nw(n为整数)。

原本的CTFT：

离散化：

把To看作单位1，则离散傅里叶变换：

之所以积分从无穷变成0~2pi，原因与离散傅里叶级数展开类似，离散对周期，频谱图应该为周期函数。

同样的方法，我们也可以推导反离散傅里叶变换：

注意哈，F并不是一个数，它的个数是和k有关的。在写这篇文章前没有预先理清楚八个公式的各种符号，看着有点乱，我滴锅~~每一个k都对应一个F。待会儿呈上代码，小伙伴们应该就会很清楚啦。

说完了离散傅里叶变换公式的推导，再说一说模拟频率f吧。在之前就说过，模拟频率f需要在DFT中用到，这是因为DFT计算出的频率谱是离散的，那么我们就需要一个最小间隔，也就是频率谱横轴的最小单位，这个最小单位就是模拟频率f。

模拟频率f的公式：

fs代表采样频率，N代表一个周期内的采样数。

这个公式的推导非常简单：

此公式中的T代表要分解的函数的周期，而To是采样周期，采样周期是采样频率的倒数，因此能推出模拟频率f的公式。

得到了f，我们就得到了频率谱的横坐标，而纵坐标又是什么呢？懂得小伙伴肯定知道，纵坐标就是振幅，其大小就和系数an和bn相关，也就是蕴含在我们的指数虚数e当中。

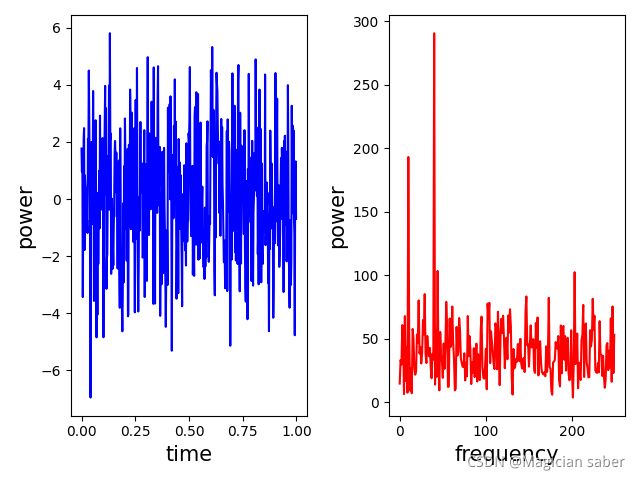
做一个离散傅里叶变换实例，大家伙就都明白了。

比如：

有一个波形y：

采样周期：T = (0:nt-1)/fs

采样频率：fs = 500
采样数：nt = 500
频谱：K = (0:nt/2)'*fs/nt

x = 0.7*sin(2*pi*10*T) + sin(2*pi*40*T);
y = x + 2*np.random.randn(size(T))
 

请对y做离散傅里叶变换并画出频谱K对应的振幅图。

这里面的fs/nt就是我们上面说的模拟频率f，也就是频谱图横坐标的单位。上面的这些式子都是python里的代码直接粘贴过来的（实属本人太懒）。

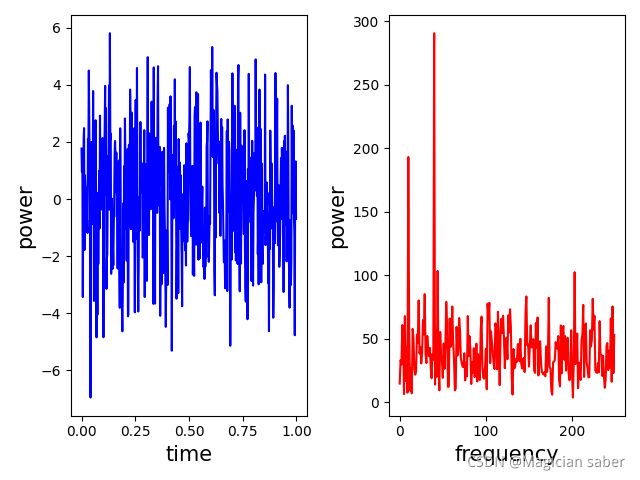
代码部分会贴在这篇文章最底下，这里先给小伙伴们看看处理后的图像，左侧为原波形，右侧为K对应的频谱图。

 我的单位计算是有问题的，大家看看图像，明白原理就好。

然后我又用np的fft，就是快速傅里叶变换做了一个图像，两者是一模一样的（前面说了这么多原理和推导，其实做到最后只要直接调用np的fft函数即可，比自己写DFT的代码简单方便多了）：

 以上就是“傅里叶级数和傅里叶变换详细推导及其在python的应用”的全部内容，如果觉得还不错记得给个赞嗷，先谢谢各位看到这里啦。

可能在写代码的时候会用到积分等数学方法，如何在python中实现，可以看看这个用sympy库的大佬：

(64条消息) Python 中的Sympy详细介绍_Cheney_渣渣杰 的博客-CSDN博客_sympy

代码部分：

拟合三角波代码：

import matplotlib.pyplot as plt
import numpy as np
from sympy import *
#三角波形を描く
plt.subplot(1,2,1)
for i in range(-3,3,1):
    x = np.arange(i,i+1,0.01)
    dx = np.where(x<=i+0.5,abs(i-x),1-abs(i-x))
    y = np.sqrt(3)*dx
    plt.plot(x,y,"b")


#フーリエ級数(CTFS)の逆変換と三角波形のフィッティング
plt.subplot(1,2,2)
N = 8
t = symbols("t")
ft_1 = np.sqrt(3)*t
ft_2=  np.sqrt(3)*(1-t)
T = 1
b0 =np.sqrt(3)/2
Fx = b0
an,bn = [0],[b0]
for i in range(1,N):
    An = 2/T*(integrate((ft_1)*sin(2*t*np.pi*i),(t,0,0.5))
            +integrate((ft_2)*sin(2*t*np.pi*i),(t,0.5,1)))
    Bn = 2/T*(integrate((ft_1)*cos(2*t*np.pi*i),(t,0,0.5))
            +integrate((ft_2)*cos(2*t*np.pi*i),(t,0.5,1)))
    an.append(An)
    bn.append(Bn)

x_fourier = np.arange(-3,3,0.01)
for i in range(1,N):
    Fx = Fx + bn[i]*np.cos(2*np.pi*i*x_fourier/T) + an[i]*np.sin(2*np.pi*i*x_fourier/T)

plt.plot(x_fourier,Fx,"g")
plt.show()

拟合矩形波代码：

import matplotlib.pyplot as plt
import numpy as np
from sympy import *

#矩形波を描く
plt.subplot(1,2,1)
for i in range(-5,5,2):
    x = np.arange(i-0.5,i+1.5,0.01)
    y = np.where((x=i),1,0)
    plt.plot(x,y,"b")


#フーリエ級数(CTFS)の逆変換と矩形波のフィッティング
plt.subplot(1,2,2)
N = 500
t = symbols("t")
ft_1 = 1
ft_2=  0
T = 2
b0 =0.5
Fx = b0
an,bn = [0],[b0]
for i in range(1,N):
    An = 2/T* integrate((ft_1)*sin(t*np.pi*i),(t,1,2))
    Bn = 2/T* integrate((ft_1)*cos(t*np.pi*i),(t,1,2))
    an.append(An)
    bn.append(Bn)

x_fourier = np.arange(-5,5,0.01)
for i in range(1,N):
    Fx = Fx + bn[i]*np.cos(2*np.pi*i*x_fourier/T) + an[i]*np.sin(2*np.pi*i*x_fourier/T)

plt.plot(x_fourier,Fx,"d")
plt.show()

对y做DFT：

import numpy as np
import matplotlib.pyplot as plt

#波形図を描く
plt.subplot(121)
fs = 500
nt = 500
T = np.arange(0,nt)/fs
K = np.arange(0,nt/2)*fs/nt
w = 2*np.pi/nt
np.random.seed(20)
x = 0.7*np.sin(2*np.pi*10*T) + np.sin(2*np.pi*40*T)
y = x + 2*np.random.randn(np.size(T))
plt.xlabel("time",fontsize = 15)
plt.ylabel("power",fontsize = 15)
plt.plot(T,y,"b")


#DFTの開始
plt.subplot(122)
P = []
k = 0
for j in range(len(K)):
    fi = 0
    for i in range(nt):
        fi += y[i] * np.exp(-1j * w * i * k)
    cosi, sini = np.real(fi), np.imag(fi)
    power = np.sqrt(cosi ** 2 + sini ** 2)  # sinx+cosx　の振幅を計算する
    P.append(power)
    k += 1

P = np.array(P)
plt.plot(K,P,"r")
plt.xlabel("frequency",fontsize = 15)
plt.ylabel("power",fontsize = 15)
plt.show()

对y做fft：

import numpy as np
import matplotlib.pyplot as plt

#波形図を描く
plt.subplot(121)
fs = 500
nt = 500
T = np.arange(0,nt)/fs
K = np.arange(0,nt/2)*fs/nt
w = 2*np.pi/nt
np.random.seed(20)
x = 0.7*np.sin(2*np.pi*10*T) + np.sin(2*np.pi*40*T)
y = x + 2*np.random.randn(np.size(T))
plt.xlabel("time",fontsize = 15)
plt.ylabel("power",fontsize = 15)
plt.plot(T,y,"b")

plt.subplot(122)
fft_y = np.fft.fft(y)
yf = np.abs(fft_y)
yf = yf[0:len(K)]
plt.xlabel("frequency",fontsize = 15)
plt.ylabel("power",fontsize = 15)
plt.plot(K,yf,"r")
plt.show()