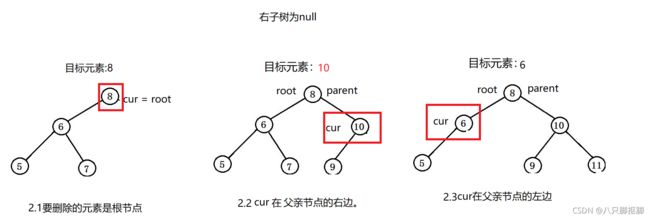
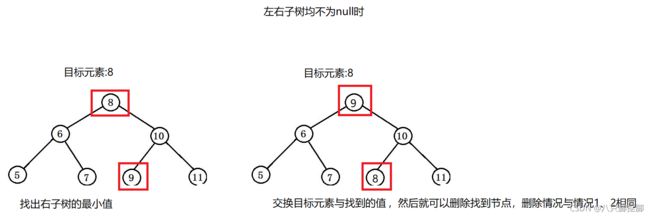
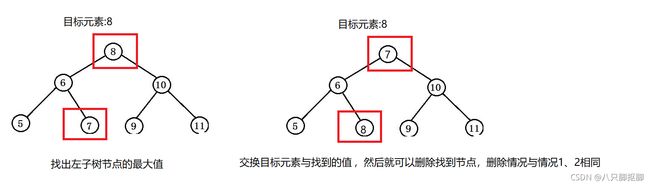
一、什么是宏函数?通过宏定义的函数是宏函数。如下,编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
Long类型前后端数据不一致
igotyback
前端
响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题,尤其是当后端使用Java的Long类型(64位)与前端JavaScript的Number类型(最大安全整数为2^53-1,即16位)进行数据交互时,很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
LocalDateTime 转 String
igotyback
java开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
Linux下QT开发的动态库界面弹出操作(SDL2)
13jjyao
QT类qt开发语言sdl2linux
需求:操作系统为linux,开发框架为qt,做成需带界面的qt动态库,调用方为java等非qt程序难点:调用方为java等非qt程序,也就是说调用方肯定不带QApplication::exec(),缺少了这个,QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出);这与qt调用本身qt库是有本质的区别的思路:1.调用方缺QApplication::exec(),那么我们在接口
店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码
说私域
人工智能小程序
摘要:本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合,阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇,提升了用户信任感、拓展了营销渠道,并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展,社区团购作为一种新兴的商业模式,在满足消费者日常需
第一场雪
岁月静好_nx
早晨起来,外面白茫茫的一片,总算是下雪了,这还是今年第一场雪呢!走在路上,踩着雪“咯吱咯吱”的,空气很湿润。树上、草坪上、屋顶上都落了白白的一层,天上还零星漂着几点雪。慢慢走在路上,呼吸着清新的空气,感受着冬天的美好,心情也好多了。
山东大学小树林支教调研团青青仓木队——翟晓楠
山东大学青青仓木队
过了半年,又一次启程,又一次回到支教的初心之地。比起上一次的试探与不安,我更多了一丝稳重与熟练。心境、处境也都随着半个学期的过去而变得不同,半个学期中,身体上的,心理上的,太多的逆境让我变得步履维艰,曲曲折折,弯弯绕绕,我仿佛打不起精神,没有胃口,没有动力。感觉走的不顺畅的时候,支教这个旅程,给了我力量。自告奋勇承担起队长这一职务的我,从组织时的复杂和困难的经历,协调各种问题,从无到有,和校长和队
2018/02/12
Tracy_zhang
人生并不在于获取,更在于放得下。放下一粒种子,收获一棵大树;放下一处烦恼,收获一个惊喜;放下一种偏见,收获一种幸福;放下一种执著,收获一种自在。放下既是一种理性抉择,也是一种豁达美。只要看得开放得下,何愁没有快乐的春莺在啼鸣,何愁没有快乐的泉溪在歌唱,何愁没有快乐的鲜花绽放!
DIV+CSS+JavaScript技术制作网页(旅游主题网页设计与制作)云南大理
STU学生网页设计
网页设计期末网页作业html静态网页html5期末大作业网页设计web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业:【HTML5网页期末作业(1000套)】程序员有趣的告白方式:【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面:计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
【华为OD机试真题2023B卷 JAVA&JS】We Are A Team
若博豆
java算法华为javascript
华为OD2023(B卷)机试题库全覆盖,刷题指南点这里WeAreATeam时间限制:1秒|内存限制:32768K|语言限制:不限题目描述:总共有n个人在机房,每个人有一个标号(1<=标号<=n),他们分成了多个团队,需要你根据收到的m条消息判定指定的两个人是否在一个团队中,具体的:1、消息构成为:abc,整数a、b分别代
数组去重
好奇的猫猫猫
整理自js中基础数据结构数组去重问题思考?如何去除数组中重复的项例如数组:[1,3,4,3,5]我们在做去重的时候,一开始想到的肯定是,逐个比较,外面一层循环,内层后一个与前一个一比较,如果是久不将当前这一项放进新的数组,挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低,代码量还多,思考?有没有更好的方法这时候不禁一想当然有了!!!hashtable啊,通过对象的hash办法
春季养肝正当时
dxn悟
重温快乐2023年2月4日立春。春天来了,春暖花开,小鸟欢唱,那在这样的季节我们如何养肝呢?自然界的春季对应中医五行的木,人体五脏肝属木,“木曰曲直”,是以树干曲曲直直地向上、向外伸长舒展的生发姿态,来形容具有生长、升发、条达、舒畅等特征的食物及现象。根据中医天人相应的理念,肝五行属木,喜条达,主疏泄,与春天相应,所以春天最适合养肝。养肝首先要少生气,因为肝喜条达恶抑郁。人体五志肝为怒,生气发怒最
关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript
二挡起步
web前端期末大作业javascripthtmlcss旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业,Web大学生网页HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
HTML网页设计制作大作业(div+css) 云南我的家乡旅游景点 带文字滚动
二挡起步
web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript:做与用户的交互行为文章目录前端学习路线
Day17笔记-高阶函数
~在杰难逃~
Python笔记python开发语言pycharm数据分析
高阶函数【重点掌握】函数的本质:函数是一个变量,函数名是一个变量名,一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数,B函数调用完成之后,会得到一个结果,则B函数被称为高阶函数常用的高阶函数:map(),reduce(),filter(),sorted()1.map()map(func,iterable),返回值是一个iterator【容器,迭代器】func:函数iterab
python八股文面试题分享及解析(1)
Shawn________
python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果:21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型,不仅仅改变
每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
2023-10-22
奥雷里亚诺第n
昨天在B站看到关于猫喜欢挠人的视频,视频教导说猫挠人的话就抓住它的后脖颈然后用手打打挠人的那个爪子。视频本身没什么,但评论区却炸开了锅(真是符合挑食者厌食心理)。令我印象最深刻的一个甚至上升到了关于我是谁这种终极问题。它说,猫就是畜生,它挠人就打它别惯着它,反正我六道轮回成了人就应该保持人的高贵,谁都别想来打破。我顿时汗颜,但看到下面全是类似的言论只不过后面的理由各有不同,本来想骂人的心都凉了一半
node.js学习
小猿L
node.jsnode.js学习vim
node.js学习实操及笔记温故node.js,node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vuereactangular离不开node.jsnode.js是什么官网:node.js是一个开源的、跨平台的运行JavaScript的运行
回溯算法-重新安排行程
chirou_
算法数据结构图论c++图搜索
leetcode332.重新安排行程这题我还没自己ac过,只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多,用什么数据结构去存数据,去读取数据,都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
2018-12-29
枫叶红时总多离别
2018年12月29日星期六昨天老师就告诉我们,今天下午不用上课,是图书漂流活动会。我觉得很兴奋,好期待。到了下午,我帮好忙就到外面去买书,刚一出去,就有一大帮的大哥哥、大姐姐围着我问要不要买书,买一本书送一颗糖。我看到了一本《小老虎比上树》的书,问大姐姐多少钱,大姐姐说这本书原价13块,现在便宜4块钱也就是9块钱卖给你,我就把一张10块钱给她找,她找了我一块钱。我现在想想我今天只带了10块钱,现
Redis系列:Geo 类型赋能亿级地图位置计算
Ly768768
redisbootstrap数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构,它是基于不同业务场景而设计的:动态字符串(REDIS_STRING):整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
Faiss:高效相似性搜索与聚类的利器
网络·魚
大数据faiss
Faiss是一个针对大规模向量集合的相似性搜索库,由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构,用于加速向量之间的相似性搜索,特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理:近似最近邻搜索:Faiss的核心功能之一是近似最近邻搜索,它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的,
似乎老是忘记什么东西
灰台
S带上了耳机,眼前的一切都与她隔绝开来。虽是初春的好天气,花都开的正鲜艳,行人也都驻足欣赏,还有不少怀着好心情的年轻人在花树下打闹。不过S似乎并不在意这些,连耳机传来的rap也没有调动起她的兴致。一瞬间,心脏好像变成了黑洞,“啊,我身边还有几个人呢,似乎没有了吧”。阳光的温度覆盖到了脖子上,S抬头看了看开满花的树,“我妈好像还挺喜欢花的”,S随手拍了一张照片,微信发到自己一家三口的群里。过了一会,
《在战“疫”中成长致敬生活》观后感
梅子刘的刀
(作者:周晨)今天上午,我看了“我是接班人”网络大课堂《在战役中成长致敬生活》。有很多人拿出自己攒下的钱,默默地捐给了武汉,有几千块钱的、有几万块钱的,也有十几万块钱的。连小朋友也把自己的压岁钱捐给了武汉。有名环卫工人把自己五年的积蓄全部捐给了武汉。有名外卖小哥为医护人员买鞋子送吃的。还有已经治愈出院的新型肺炎病人捐了400毫升的血浆。还有位叫大树的叔叔,虽然他没有钱,但是他地里有蔬菜,捐了几大卡
2019-08-16
希望在东方
《春游荣华山》春游荣华山,乍暖还寒。青苔路,石阶险。山路弯上弯!为寻古寺往幽探。细雨已润江南岸,初春芳草现。老树新芽冒枝端,人间又过到新年。今游荣华山,树茂参天,古寺悠闲。细雨飘落发端!三眼井旁,投币许心愿,并祷一世安然。更喜大女明事端,应心安,放开颜。修竹静默,雨中吐心愿。待得春风浩吹时,春笋节节攀。图片发自App图片发自App图片发自App
《我的青葱岁月之缘来是你》 第二章 迎新晚会
思源思缘思怨
“怎么你也来了这里?”我愉快的问到,想着这是上天给的缘分吗?我还没去找他竟然就相遇了。那个让我开心的老乡。“你好,我也是舞蹈社的新人啊!”他说,笑起来回答我,眼睛弯弯的。“这么巧,我叫吴倩,你叫啥?”“我叫韩欢,你也是B市人吧,c中毕业的?”“我不是,我是f中的,不然肯定会认识你的”“是吗?以后多多关照了”他还冲我眨了眨眼睛。内心一阵悸动,这是……回到寝室,我兴奋的告诉我的室友这个事情,我再次觉得
数据结构之哈希表
X同学的开始
数据结构数据结构散列表
哈希表(散列表)出现的原因在顺序表中查找时,需要从表头开始,依次遍历比较a[i]与key的值是否相等,直到相等才返回索引i;在有序表中查找时,我们经常使用的是二分查找,通过比较key与a[i]的大小来折半查找,直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是,这两种方法的效率都依赖于查找中比较的次数。我们有一种想法,能不能不经过比较,而是直接通过关键字key一次得到所要的结果呢?这时,
Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
java责任链模式
3213213333332132
java责任链模式村民告县长
责任链模式,通常就是一个请求从最低级开始往上层层的请求,当在某一层满足条件时,请求将被处理,当请求到最高层仍未满足时,则请求不会被处理。
就是一个请求在这个链条的责任范围内,会被相应的处理,如果超出链条的责任范围外,请求不会被相应的处理。
下面代码模拟这样的效果:
创建一个政府抽象类,方便所有的具体政府部门继承它。
package 责任链模式;
/**
*
linux、mysql、nginx、tomcat 性能参数优化
ronin47
一、linux 系统内核参数
/etc/sysctl.conf文件常用参数 net.core.netdev_max_backlog = 32768 #允许送到队列的数据包的最大数目
net.core.rmem_max = 8388608 #SOCKET读缓存区大小
net.core.wmem_max = 8388608 #SOCKET写缓存区大
php命令行界面
dcj3sjt126com
PHPcli
常用选项
php -v
php -i PHP安装的有关信息
php -h 访问帮助文件
php -m 列出编译到当前PHP安装的所有模块
执行一段代码
php -r 'echo "hello, world!";'
php -r 'echo "Hello, World!\n";'
php -r '$ts = filemtime("
Filter&Session
171815164
session
Filter
HttpServletRequest requ = (HttpServletRequest) req;
HttpSession session = requ.getSession();
if (session.getAttribute("admin") == null) {
PrintWriter out = res.ge
连接池与Spring,Hibernate结合
g21121
Hibernate
前几篇关于Java连接池的介绍都是基于Java应用的,而我们常用的场景是与Spring和ORM框架结合,下面就利用实例学习一下这方面的配置。
1.下载相关内容: &nb
[简单]mybatis判断数字类型
53873039oycg
mybatis
昨天同事反馈mybatis保存不了int类型的属性,一直报错,错误信息如下:
Caused by: java.lang.NumberFormatException: For input string: "null"
at sun.mis
项目启动时或者启动后ava.lang.OutOfMemoryError: PermGen space
程序员是怎么炼成的
eclipsejvmtomcatcatalina.sheclipse.ini
在启动比较大的项目时,因为存在大量的jsp页面,所以在编译的时候会生成很多的.class文件,.class文件是都会被加载到jvm的方法区中,如果要加载的class文件很多,就会出现方法区溢出异常 java.lang.OutOfMemoryError: PermGen space.
解决办法是点击eclipse里的tomcat,在
我的crm小结
aijuans
crm
各种原因吧,crm今天才完了。主要是接触了几个新技术:
Struts2、poi、ibatis这几个都是以前的项目中用过的。
Jsf、tapestry是这次新接触的,都是界面层的框架,用起来也不难。思路和struts不太一样,传说比较简单方便。不过个人感觉还是struts用着顺手啊,当然springmvc也很顺手,不知道是因为习惯还是什么。jsf和tapestry应用的时候需要知道他们的标签、主
spring里配置使用hibernate的二级缓存几步
antonyup_2006
javaspringHibernatexmlcache
.在spring的配置文件中 applicationContent.xml,hibernate部分加入
xml 代码
<prop key="hibernate.cache.provider_class">org.hibernate.cache.EhCacheProvider</prop>
<prop key="hi
JAVA基础面试题
百合不是茶
抽象实现接口String类接口继承抽象类继承实体类自定义异常
/* * 栈(stack):主要保存基本类型(或者叫内置类型)(char、byte、short、 *int、long、 float、double、boolean)和对象的引用,数据可以共享,速度仅次于 * 寄存器(register),快于堆。堆(heap):用于存储对象。 */ &
让sqlmap文件 "继承" 起来
bijian1013
javaibatissqlmap
多个项目中使用ibatis , 和数据库表对应的 sqlmap文件(增删改查等基本语句),dao, pojo 都是由工具自动生成的, 现在将这些自动生成的文件放在一个单独的工程中,其它项目工程中通过jar包来引用 ,并通过"继承"为基础的sqlmap文件,dao,pojo 添加新的方法来满足项
精通Oracle10编程SQL(13)开发触发器
bijian1013
oracle数据库plsql
/*
*开发触发器
*/
--得到日期是周几
select to_char(sysdate+4,'DY','nls_date_language=AMERICAN') from dual;
select to_char(sysdate,'DY','nls_date_language=AMERICAN') from dual;
--建立BEFORE语句触发器
CREATE O
【EhCache三】EhCache查询
bit1129
ehcache
本文介绍EhCache查询缓存中数据,EhCache提供了类似Hibernate的查询API,可以按照给定的条件进行查询。
要对EhCache进行查询,需要在ehcache.xml中设定要查询的属性
数据准备
@Before
public void setUp() {
//加载EhCache配置文件
Inpu
CXF框架入门实例
白糖_
springWeb框架webserviceservlet
CXF是apache旗下的开源框架,由Celtix + XFire这两门经典的框架合成,是一套非常流行的web service框架。
它提供了JAX-WS的全面支持,并且可以根据实际项目的需要,采用代码优先(Code First)或者 WSDL 优先(WSDL First)来轻松地实现 Web Services 的发布和使用,同时它能与spring进行完美结合。
在apache cxf官网提供
angular.equals
boyitech
AngularJSAngularJS APIAnguarJS 中文APIangular.equals
angular.equals
描述:
比较两个值或者两个对象是不是 相等。还支持值的类型,正则表达式和数组的比较。 两个值或对象被认为是 相等的前提条件是以下的情况至少能满足一项:
两个值或者对象能通过=== (恒等) 的比较
两个值或者对象是同样类型,并且他们的属性都能通过angular
java-腾讯暑期实习生-输入一个数组A[1,2,...n],求输入B,使得数组B中的第i个数字B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]
bylijinnan
java
这道题的具体思路请参看 何海涛的微博:http://weibo.com/zhedahht
import java.math.BigInteger;
import java.util.Arrays;
public class CreateBFromATencent {
/**
* 题目:输入一个数组A[1,2,...n],求输入B,使得数组B中的第i个数字B[i]=A
FastDFS 的安装和配置 修订版
Chen.H
linuxfastDFS分布式文件系统
FastDFS Home:http://code.google.com/p/fastdfs/
1. 安装
http://code.google.com/p/fastdfs/wiki/Setup http://hi.baidu.com/leolance/blog/item/3c273327978ae55f93580703.html
安装libevent (对libevent的版本要求为1.4.
[强人工智能]拓扑扫描与自适应构造器
comsci
人工智能
当我们面对一个有限拓扑网络的时候,在对已知的拓扑结构进行分析之后,发现在连通点之后,还存在若干个子网络,且这些网络的结构是未知的,数据库中并未存在这些网络的拓扑结构数据....这个时候,我们该怎么办呢?
那么,现在我们必须设计新的模块和代码包来处理上面的问题
oracle merge into的用法
daizj
oraclesqlmerget into
Oracle中merge into的使用
http://blog.csdn.net/yuzhic/article/details/1896878
http://blog.csdn.net/macle2010/article/details/5980965
该命令使用一条语句从一个或者多个数据源中完成对表的更新和插入数据. ORACLE 9i 中,使用此命令必须同时指定UPDATE 和INSE
不适合使用Hadoop的场景
datamachine
hadoop
转自:http://dev.yesky.com/296/35381296.shtml。
Hadoop通常被认定是能够帮助你解决所有问题的唯一方案。 当人们提到“大数据”或是“数据分析”等相关问题的时候,会听到脱口而出的回答:Hadoop! 实际上Hadoop被设计和建造出来,是用来解决一系列特定问题的。对某些问题来说,Hadoop至多算是一个不好的选择,对另一些问题来说,选择Ha
YII findAll的用法
dcj3sjt126com
yii
看文档比较糊涂,其实挺简单的:
$predictions=Prediction::model()->findAll("uid=:uid",array(":uid"=>10));
第一个参数是选择条件:”uid=10″。其中:uid是一个占位符,在后面的array(“:uid”=>10)对齐进行了赋值;
更完善的查询需要
vim 常用 NERDTree 快捷键
dcj3sjt126com
vim
下面给大家整理了一些vim NERDTree的常用快捷键了,这里几乎包括了所有的快捷键了,希望文章对各位会带来帮助。
切换工作台和目录
ctrl + w + h 光标 focus 左侧树形目录ctrl + w + l 光标 focus 右侧文件显示窗口ctrl + w + w 光标自动在左右侧窗口切换ctrl + w + r 移动当前窗口的布局位置
o 在已有窗口中打开文件、目录或书签,并跳
Java把目录下的文件打印出来
蕃薯耀
列出目录下的文件文件夹下面的文件目录下的文件
Java把目录下的文件打印出来
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年7月11日 11:02:
linux远程桌面----VNCServer与rdesktop
hanqunfeng
Desktop
windows远程桌面到linux,需要在linux上安装vncserver,并开启vnc服务,同时需要在windows下使用vnc-viewer访问Linux。vncserver同时支持linux远程桌面到linux。
linux远程桌面到windows,需要在linux上安装rdesktop,同时开启windows的远程桌面访问。
下面分别介绍,以windo
guava中的join和split功能
jackyrong
java
guava库中,包含了很好的join和split的功能,例子如下:
1) 将LIST转换为使用字符串连接的字符串
List<String> names = Lists.newArrayList("John", "Jane", "Adam", "Tom");
Web开发技术十年发展历程
lampcy
androidWeb浏览器html5
回顾web开发技术这十年发展历程:
Ajax
03年的时候我上六年级,那时候网吧刚在小县城的角落萌生。传奇,大话西游第一代网游一时风靡。我抱着试一试的心态给了网吧老板两块钱想申请个号玩玩,然后接下来的一个小时我一直在,注,册,账,号。
彼时网吧用的512k的带宽,注册的时候,填了一堆信息,提交,页面跳转,嘣,”您填写的信息有误,请重填”。然后跳转回注册页面,以此循环。我现在时常想,如果当时a
架构师之mima-----------------mina的非NIO控制IOBuffer(说得比较好)
nannan408
buffer
1.前言。
如题。
2.代码。
IoService
IoService是一个接口,有两种实现:IoAcceptor和IoConnector;其中IoAcceptor是针对Server端的实现,IoConnector是针对Client端的实现;IoService的职责包括:
1、监听器管理
2、IoHandler
3、IoSession
ORA-00054:resource busy and acquire with NOWAIT specified
Everyday都不同
oraclesessionLock
[Oracle]
今天对一个数据量很大的表进行操作时,出现如题所示的异常。此时表明数据库的事务处于“忙”的状态,而且被lock了,所以必须先关闭占用的session。
step1,查看被lock的session:
select t2.username, t2.sid, t2.serial#, t2.logon_time
from v$locked_obj
javascript学习笔记
tntxia
JavaScript
javascript里面有6种基本类型的值:number、string、boolean、object、function和undefined。number:就是数字值,包括整数、小数、NaN、正负无穷。string:字符串类型、单双引号引起来的内容。boolean:true、false object:表示所有的javascript对象,不用多说function:我们熟悉的方法,也就是
Java enum的用法详解
xieke90
enum枚举
Java中枚举实现的分析:
示例:
public static enum SEVERITY{
INFO,WARN,ERROR
}
enum很像特殊的class,实际上enum声明定义的类型就是一个类。 而这些类都是类库中Enum类的子类 (java.l