【算法】交换排序——快速排序+冒泡排序(更新了非递归冒泡以及优化)
之前介绍的排序算法:
- 【算法】插入排序——希尔排序+直接插入排序_Rinne’s blog-CSDN博客
- 【算法】选择排序——堆排序+直接选择排序_Rinne’s blog-CSDN博客
交换排序
所谓交换,旨在将较大元素向尾部移动,较小元素向前移动
文章目录
- 交换排序
-
- 一、冒泡排序
-
- 1. 算法原理
- 2. 图解原理
- 3. 代码实现
- 4. 测试
- 5. 性能对比
- 二、单趟快速排序
-
- 1. 算法原理
- 2. hoare版本
-
- 图解原理
- 代码实现
- 测试
- 代码优化
- 3. 挖坑法
-
- 图解原理
- 代码实现
- 测试
- 4. 前后指针法
-
- 图解原理
- 代码实现
- 测试
- 三、递归快排
-
- **优化代码**
- 四、非递归快排
一、冒泡排序
1. 算法原理
-
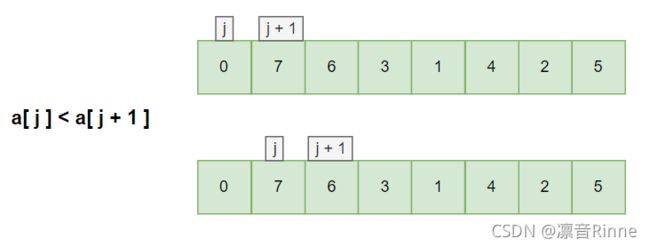
遍历元素列,比较相邻的元素。如果第一个比第二个大,就交换他们两个
-
对每一对相邻元素做同样的操作,从开始第一对到结尾的最后一对。最后,末尾元素应该会是最大的数
-
针对所有的元素重复以上的步骤,除了最后一个
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较、
2. 图解原理
设元素个数为n
以此类推,当交换n-1次的时候,最后一个数为最大的数字
再对前n-1个元素进行同样操作
最后变成有序数列
3. 代码实现
这里应注意如果拿到数列本身就是有序的,就不必循环那么多次,所以这里我们需要有个标记来判断第一次遍历就知道它是有序的
//交换函数
void swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
//冒泡排序
void BubbleSort(int* a, int n)
{
int i = 0;
int j = 0;
for (i = 0; i < n - 1; i++)
{
int flag = 0;
for (j = 0; j < n - 1 - i; j++)
{
if (a[j] > a[j + 1])
{
swap(&a[j], &a[j + 1]);
flag = 1;
}
}
if (flag == 0)
{
return;
}
}
}
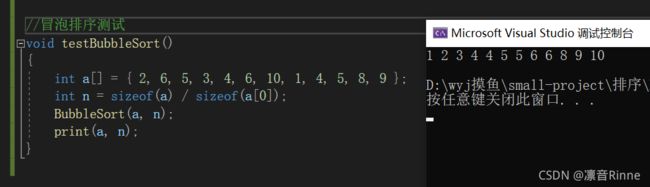
4. 测试
void testBubbleSort()
{
int a[] = {
2, 6, 5, 3, 4, 6, 10, 1, 4, 5, 8, 9 };
int n = sizeof(a) / sizeof(a[0]);
BubbleSort(a, n);
print(a, n);
}
5. 性能对比
冒泡排序
时间复杂度:O(n2)
空间复杂度:O(n)
由于前2篇文章介绍了直接插入排序和选择排序,二者时间复杂度都是O(n2)
这三者当中,按照优劣,谁更优呢?
有序数列的时候:
-
选择排序:因为选择排序要遍历找出最大和最小,不知道是否有序,所以时间复杂度还是O(n2),所以先把它放在最后
-
直接插入排序和冒泡排序:都是O(n)
接近有序数列但不是有序数列:(比如1 2 4 3)
- 直接插入排序: 比较次数
n - 冒泡排序: 比较次数
n - 1 + n - 2
二、单趟快速排序
1. 算法原理
用数组的第一个数作为关键数据,然后将所有比它小的数都放到它左边,所有比它大的数都放到它右边,这个过程称为一趟快速排序
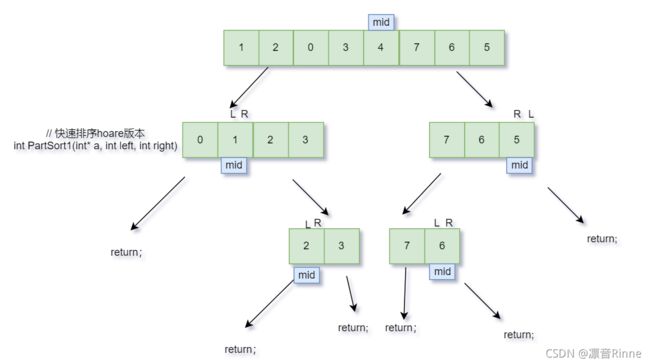
2. hoare版本
时间复杂度O(n)
图源百度
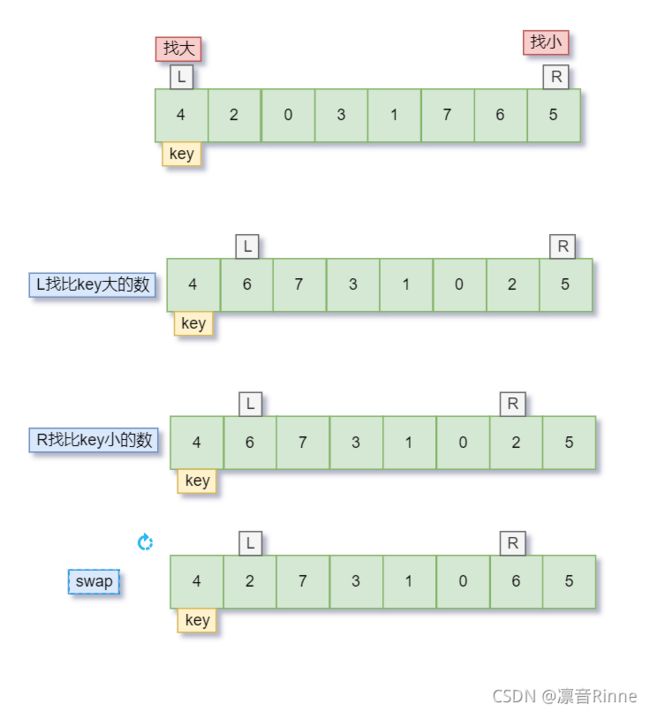
图解原理
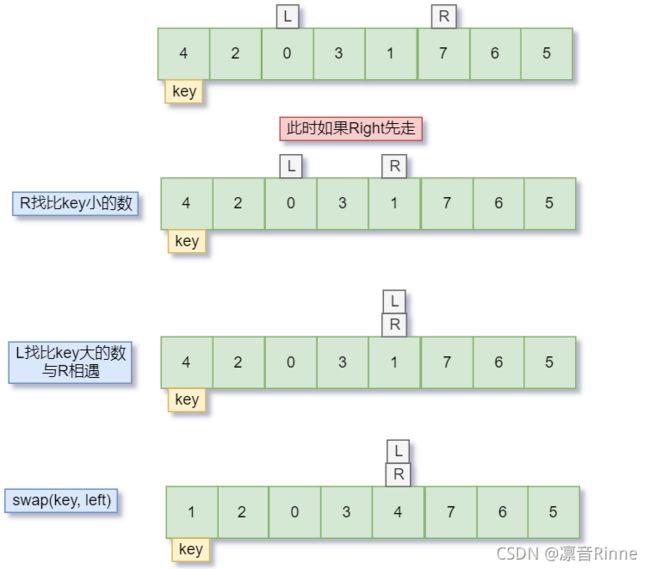
关键数字**key在左边**的时候:
Left找比key大的数字,Right找比key小的数字`
Right先走
原因等看完图解来解释
以此类推…………直到
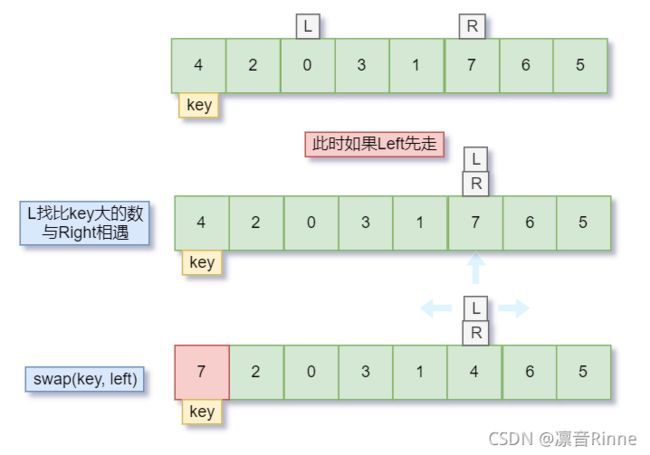
此时出现了问题,换做 Right先走呢?
这就没有问题了
在循环的最后一个环节是交换R和L,后来R的位置是比key大的数,L的位置是比key小的数
我们需要L和R相遇的位置上是比key小的数
所以需要R遇上L
- 最乐观的是R先走,如果在此之前R找到比key小的数也不亏
- 下一步最乐观的是让L遇到R,如果在此之前L遇到比key大的数字
- R和L交换后进入下一个循环(一般情况)
还需注意
当数列是同一个元素的时候,注意判断的边界,不然会出现死循环
代码实现
这里方便测试写成void形式,具体放在递归中看递归快排部分
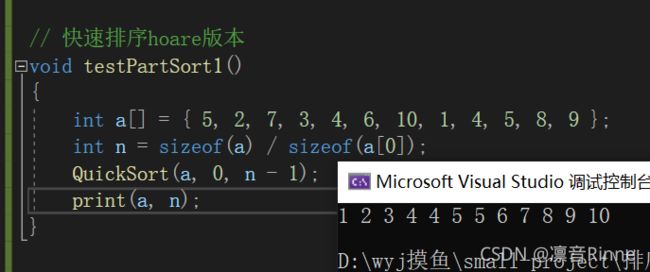
// 快速排序hoare版本
void PartSort1(int* a, int left, int right)
{
int key = left;
while (left < right)
{
while (a[right] >= a[key] && right != left)
{
right--;
}
while (a[left] <= a[key] && right != left)
{
left++;
}
swap(&a[left], &a[right]);
}
swap(&a[left], &a[key]);
}
测试
代码优化
如果一个数列是有序数列,R先走,最后时间复杂度是O(n2)
达不到我们想要的O(n)
要么
-
随机选
mid但还是有可能发生选成了有序数列
-
三数取中
针对有序,取left,mid,right中不是最大也不是最小的那个
int GetMidIndex(int* a, int left, int right) { int mid = left + ((right - left) >> 1); if (a[left] < a[mid]) { if (a[mid] < a[right]) { return mid; } else if (a[left] > a[right]) { return left; } else { return right; } } else { if (a[mid] > a[right]) { return mid; } else if (a[left] < a[right]) { return left; } else { return right; } } }
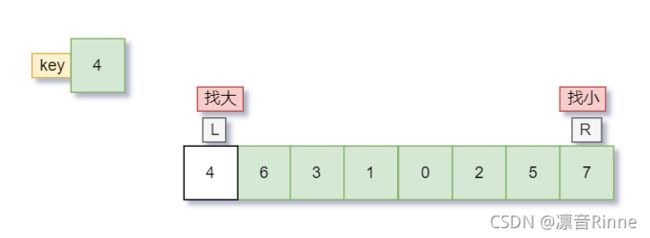
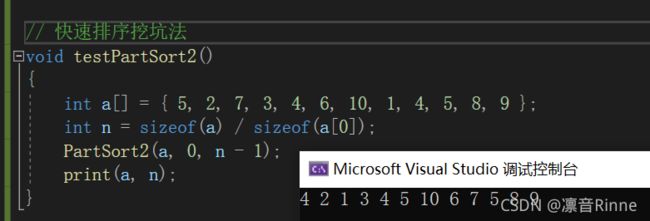
3. 挖坑法
原理跟hoare法差不多,只是刚开始先把key保存起来,最后一步的时候也是将 key放在R 和 L 相遇的位置
图解原理
顺序也是R先开始,理由和hoare法相同
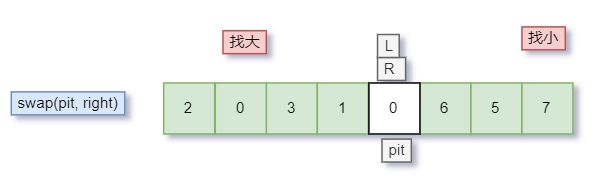
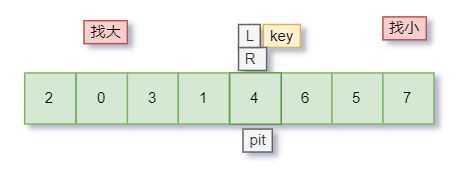
以此类推……直到L和R相遇了
再将刚才的 key,放入坑中
代码实现
这里方便测试写成void形式,具体放在递归中看递归快排部分
// 快速排序挖坑法
void PartSort2(int* a, int left, int right)
{
int key = a[left];
int pit = left;
while (left < right)
{
while (a[right] >= key && right != left)
{
right--;
}
a[pit] = a[right];
pit = right;
while (a[left] <= key && right != left)
{
left++;
}
a[pit] = a[left];
pit = left;
}
a[pit] = key;
}
测试
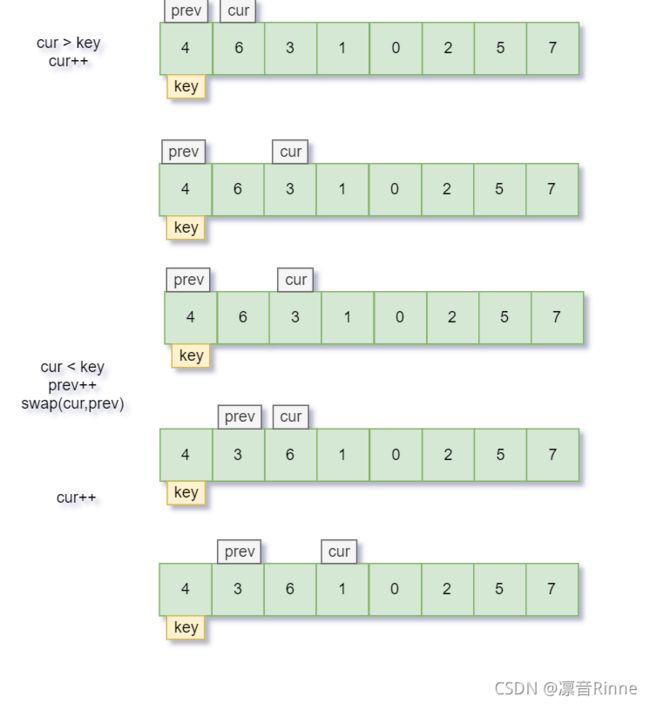
4. 前后指针法
和hoare一样也是有个key值
图解原理
直到cur越界退出循环
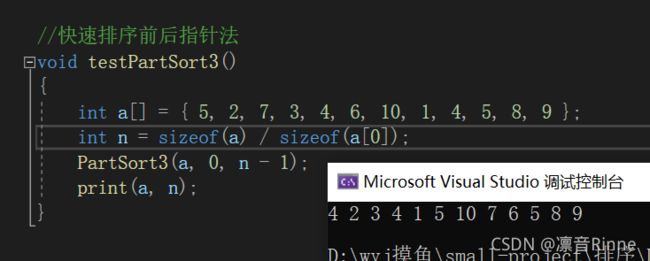
代码实现
这里方便测试写成void形式,具体放在递归中看递归快排部分
// 快速排序前后指针法
void PartSort3(int* a, int left, int right)
{
int key = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[key] && ++prev != cur)
//这里如果前面不满足的话不会执行后面
{
swap(&a[cur], &a[prev]);
}
cur++;
}
swap(&a[key], &a[prev]);
}
测试
三、递归快排
前面介绍了3种单趟排序的方法
快排的思想其实用到了之前有一篇文章所提及的分治算法思想
- 【LeetCode·位运算.190】颠倒二进制位,一题感受分治算法妙用,题目分析+两种思路+知识点总结_Rinne’s blog-CSDN博客
分治,分治,分而治之
以hoare版本为例
时间复杂度 O(n*logn)
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{
int key = left;
while (left < right)
{
while (a[right] >= a[key] && right != left)
{
right--;
}
while (a[left] <= a[key] && right != left)
{
left++;
}
swap(&a[left], &a[right]);
}
swap(&a[left], &a[key]);
return left;
}
//快排
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int mid = PartSort1(a, left, right);
QuickSort(a, left, mid - 1);
QuickSort(a, mid + 1, right);
}
优化代码
因为是递归调用,调用函数次数越往后,调用次数成指数增长,占用栈空间大小
对于最后10个数,我们不进行快排,进行插入排序(时间复杂度差不多),但不需要递归
//快排
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
//小区间优化
if (right - left + 1 <= 10)
{
InsertSort(a + left, right - left + 1);
}
else
{
//int mid = PartSort1(a, left, right);
//int mid = PartSort2(a, left, right);
int mid = PartSort3(a, left, right);
QuickSort(a, left, mid - 1);
QuickSort(a, mid + 1, right);
}
}
性能测试
其他版本
// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{
//三数取中
int key = GetMidIndex(a, left, right);
swap(&a[key], &a[left]);
key = a[left];
int pit = left;
while (left < right)
{
while (a[right] >= key && right != left)
{
right--;
}
a[pit] = a[right];
pit = right;
while (a[left] <= key && right != left)
{
left++;
}
a[pit] = a[left];
pit = left;
}
a[pit] = key;
return pit;
}
// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
//三数取中
int key = GetMidIndex(a, left, right);
swap(&a[key], &a[left]);
key = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[key] && ++prev != cur)
{
swap(&a[cur], &a[prev]);
}
cur++;
}
swap(&a[key], &a[prev]);
return prev;
}
四、非递归快排
每次如果是递归实现问题,就会自然想到,非递归的话如何实现这种快排
首先我们知道递归快排是程序不断调用函数栈帧来实现的,现在我们不用递归,但要实现快排,模拟实现栈来操作
图解分析
-
紫色是我们需要的子区间,下标左<右 -
红色是无效子区间,下标左>=右
按顺序从左到右递归,用栈的方式存储数组下标,注意后进先出,右边先进,左边出
红色的不满足条件不入栈
//非递归快排
void QuickSortNonR(int* a, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
int mid = PartSort3(a, begin, end);
if (mid + 1 < end)
{
StackPush(&st, mid + 1);
StackPush(&st, end);
}
if (begin < mid - 1)
{
StackPush(&st, begin);
StackPush(&st, mid - 1);
}
}
StackDestroy(&st);
}
测试