第七章 离散傅里叶变换
离散傅里叶变换(DFT)与离散余弦变换(DCT)之间唯一的区别在于,不再使用余弦函数,而是使用负指数函数。
7.1 复指数
幂可以表示为乘幂序列,这个定义适合实数、虚数
e φ = 1 + φ + φ 2 / 2 ! + φ 3 / 3 ! + … e i φ = 1 + i φ − φ 2 / 2 ! − i φ 3 / 3 ! + … e i φ = c o s φ + i s i n φ e^{φ}=1+φ+φ^{2}/2!+φ^{3}/3!+…\\ e^{iφ}=1+iφ-φ^{2}/2!-iφ^{3}/3!+…\\ e^{iφ}=cosφ+i sinφ eφ=1+φ+φ2/2!+φ3/3!+…eiφ=1+iφ−φ2/2!−iφ3/3!+…eiφ=cosφ+isinφ
可以理解为 e i φ e^{iφ} eiφ是一个大小为1的复数,在复平面上,它总是在单位圆上,也是一个向量,与x轴正半轴的弧度角便是 φ φ φ
e α + i φ = e α e i φ = A e i φ e^{\alpha+iφ}=e^{\alpha}e^{iφ}=Ae^{iφ} eα+iφ=eαeiφ=Aeiφ
其中A是实数,意为振幅, e i φ e^{iφ} eiφ是单位复数,意为角度
NumPy提供了一个版本的exp支持复数
phi = 1.5
z = np.exp(1j * phi)#大小为1角度为φ
z.real
z.imag
abs(z)#1.0
np.absolute(z)#1.0
np.angle#1.5
7.2 复信号
e i φ ( t ) = c o s φ ( t ) + i s i n φ ( t ) e^{iφ(t)}=cosφ(t)+i sinφ(t) eiφ(t)=cosφ(t)+isinφ(t)
复正弦信号 φ ( t ) = 2 π f t φ(t)=2\pi ft φ(t)=2πft
e i 2 π f t = c o s 2 π f t + i s i n 2 π f t e^{i2\pi ft}=cos2\pi ft+i sin2\pi ft ei2πft=cos2πft+isin2πft
更一般信号可能从相位 φ 0 φ_{0} φ0开始 e i ( 2 π f t + φ 0 ) e^{i(2\pi ft+φ_{0})} ei(2πft+φ0)
实现该采样结果为复数的信号
class ComplexSinusoid(Sinusoid):
def evaluate(self, ts):
phases = PI2 * self.freq * ts + self.offset
ys = self.amp *np.exp(1j * phases)
return ys
复信号是一序列复数,如何解释它呢?这里有一个不太令人满意的答案:
它包含两个信号——实数部分和虚数部分
7.3 合成问题
给定各个复数元素的频率和振幅,如何对信号求值
方法一:创建一个ComplexSinusoid对象然后叠加它们
def synthesize1(amp, fs, ts):
components = [thinkdsp.ComplexSinusoid(freq, amp) for amp, freq in zip(amps, fs)]
signal = thinkdsp.SumSignal(*components)
ys = signal.evaluate(ts)
return ys
解释复信号
amps = np.array([0.6, 0.25, 0.1, 0.05])
fs = [100, 200, 300, 400]
framerate = 11025
ts = np.linspace(0, 1, framerate)
ys = synthesize1(amps, fs, ts)
n = 500
thinkplot.plot(ts[:n], ys[:n].real, label='real')
thinkplot.plot(ts[:n], ys[:n].imag, label='imag')

它们包含的频率元素的对应比例是一样的,对我们耳朵来说,感知是一样的,虽然实数部分的余弦波的和,虚数部分是正弦波的和。
7.4 使用矩阵合成
PI2 = np.pi * 2
def synthesize2(amps, fs, ts):
args = np.outer(ts, fs)
M = np.exp(1j * PI2 * args)
ys = np.dot(M, amps)
return ys
若复振幅和复正弦相乘
A e i φ 0 ⋅ e i 2 π f t = A e i ( 2 π f t + φ 0 ) Ae^{iφ_{0}}·e^{i2\pi ft}=Ae^{i(2\pi ft+φ_{0})} Aeiφ0⋅ei2πft=Aei(2πft+φ0)
等于将振幅乘以A,将相位加上了 φ 0 φ_{0} φ0
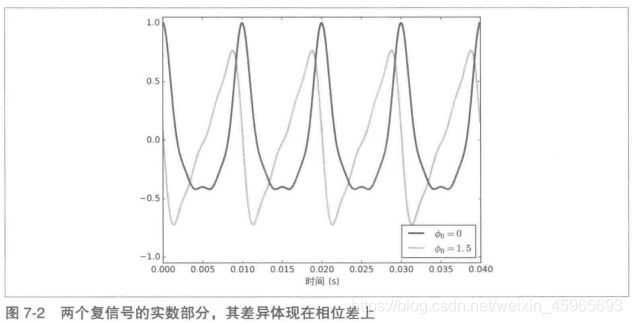
不同相位差的波形:
phi = 1.5
amps2 = amps * np.exp(1j * phi)
ys2 = synthesize2(amps2, fs, ts)
thinkplot.plot(ts[:n], ys.real[:n])
thinkplot.plot(ts[:n], ys2.real[:n])
φ 0 = 1.5 φ_{0}=1.5 φ0=1.5时各个频率元素被移动了大约十分之一个周期。但是不同频率元素的周期不同,把这些元素加和时,波形就看其了不同了
因为复振幅影响相位,相位影响波形,所以处理复振幅问题,我们就可以解决合成问题
7.5 分析问题
分析问题就是合成问题的逆命题
方法一:解线性方程组 M a = y Ma=y Ma=y
def analyze1(ys, fs, ts):
args = np.outer(ts, fs)
M = np.exp(1j * PI2 * args)
amps = np.linalg.solve(M,ys)
return amps
7.6 快速分析
DCT提速是通过选择fs和ts让M正交
DFT也是样的思路,不过对于M复数矩阵,我们需要它的酉矩阵
M的逆是M的共轭转置(转置并去每个元素虚部的负值)
N = 4
ts = np.arange(N) / N
fs = np.arange(N)
args = np.outer(ts, fs)
M = np.exp(1j * PI2 * args)
#测试M是否为酉矩阵
MstarM = M.conj().transpose().dot(M)#4I有一个额外因子N
def analyze2(ys, fs, ts):
args = np.outer(ts, fs)
M = np.exp(1j * PI2 * args)
amps = M.conj().transpose().dot(ys) / N
return amps
7.7 DFT
重写analyze,让它只接受ys,从而自行算出freq和fs
#创造一个函数来计算合成矩阵M
def synthesis_matrix(N):
ts = np.arange(N) / N
fs = np.arange(N)
args = np.outer(ts, fs)
M = np.exp(1j * PI2 * args)
return M
def analyze3(ys):
N = len(ys)
M = sythesis_matrix(N)
amps = M.conj().transpose().dot(ys) / N
return amps
def dft(ys):
N = len(ys)
M = synthesis_matrix(N)
amps = M.conj().transpose().dot(ys)
return amps
def idft(ys):
N = len(ys)
M = synthesis_matrix(N)
amps = M.dot(ys) / N
return amps
7.8 DFT是周期性的
D F T ( y ) [ k ] = ∑ n y [ n ] e x p ( − 2 π i n k / N ) D F T ( y ) [ k + N ] = ∑ n y [ n ] e x p ( − 2 π i n ( k + N ) / N ) D F T ( y ) [ k + N ] = ∑ n y [ n ] e x p ( − 2 π i n k / N ) e x p ( − 2 π i n N / N ) D F T ( y ) [ k + N ] = ∑ n y [ n ] e x p ( − 2 π i n k / N ) DFT(y)[k] = \sum_{n}y[n]exp(-2\pi ink / N)\\ DFT(y)[k+N] = \sum_{n}y[n]exp(-2\pi in(k+N) / N)\\ DFT(y)[k+N] = \sum_{n}y[n]exp(-2\pi ink / N)exp(-2\pi inN / N)\\ DFT(y)[k+N] = \sum_{n}y[n]exp(-2\pi ink / N) DFT(y)[k]=n∑y[n]exp(−2πink/N)DFT(y)[k+N]=n∑y[n]exp(−2πin(k+N)/N)DFT(y)[k+N]=n∑y[n]exp(−2πink/N)exp(−2πinN/N)DFT(y)[k+N]=n∑y[n]exp(−2πink/N)
DFT的每一个元素是一个相关,它度量的是波形数组和一个复指数在特定频率上的相似性。
7.9 实信号
np.ftt.rftt只支持实信号
本章的DFT更一般化,把这个“完全版DFT”应用到实信号:
signal = thinkdsp.SawtoothSignal(freq=500)
wave = signal.make_wave(duration=0.1,framerate=10000)
hs = dft(wave.ys)#包含波形的复DFT
amps = np.absolute(hs)#包含各个频率的振幅
#但是这些振幅对应的频率是什么呢?
#dft不知道采样率,它假设波形的持续时间为一个时间单位,假设采样率为每单位时间N次
fs = np.arange(N)
#为了得到频率,需要将随意的时间单位转换为秒
#通过这个转化,频率的范围变成了从0到实际的帧率10kHz
fs = np.arange(N) * framerate / N
#绘制频谱
thinkplot.plot(fs, amps)
thinkplot.config(xlabel='frequency (Hz)',
ylabel='amplitude')
左半部分:基频为500Hz,谐波以类似1/f的方式降低
右半部分:又开始增长,原因是因为混叠。比如,对DFT在5500Hz求值,得到的是和4500Hz一样的。
正是由于实信号的DFT在折叠频率两侧是对称的,超过这个点之后就没有什么信息了,我们可以取前一半节省时间,这也就是np.fft.rfft所做的。
声明:该系列文章是学习笔记,书名为《Python数字信号处理应用》
本书中的代码音频数据都可以从GitHub获取:https://github.com/AllenDowney/ThinkDSP
感谢支持!