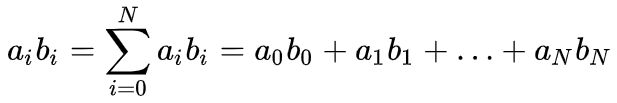Pytorch中的einsum

本文主要介绍如何使用Pytorch中的爱因斯坦求和（einsum），掌握einsum的基本用法。

einsum的安装

在安装pytorch的虚拟环境下输入以下命令：

pip install opt_einsum

 

 爱因斯坦求和约定

在数学中，爱因斯坦求和约定是一种标记法，也称为Einstein Summation Convention，在处理关于坐标的方程式时十分有效。简单来说，爱因斯坦求和就是简化掉求和式中的求和符号 ,这样就会使公式更加简洁，如

三条基本规则

einsum实现矩阵乘法的例子如下：

a = torch.randn(2, 3)
b = torch.randn(3, 4)
c = torch.mm(a, b)
d = torch.einsum("ik, kj->ij", [a, b])
print("a:{} \nb:{}".format(a, b))
print("c:{} \nd:{}".format(c, d))


# Output：
a:tensor([[ 1.7128,  0.2671, -1.5735],
        [ 0.6192,  0.0096,  1.3178]]) 
b:tensor([[ 0.0595, -1.3128,  1.6158,  0.0901],
        [ 0.9183,  1.2884,  0.6276, -0.3407],
        [ 1.2795,  1.1721,  0.7161,  1.6859]])
c:tensor([[-1.6661, -3.7489,  1.8083, -2.5894],
        [ 1.7317,  0.7440,  1.9502,  2.2741]]) 
d:tensor([[-1.6661, -3.7489,  1.8083, -2.5894],
        [ 1.7317,  0.7440,  1.9502,  2.2741]])

可以看到，c和d的输出值是一样的，c中比较好理解， torch.mm(mat1, mat2, out=None) 实现的是对矩阵mat1和mat2进行相乘。 如果mat1 是一个n×m张量，mat2 是一个 m×p 张量，将会输出一个 n×p 张量out。

那么d中呢？首先来看einsum的API：torch.einsum(equation, *operands) → Tensor。

• 第一个参数为equation，即d中的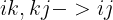，它表示了输入张量和输出张量的维度，equation中箭头左边表示输入张量，以逗号来分割每个输入张量，箭头右边则表示输出张量。表示维度的字符只能是26个英文字母，即'a'~'z'，这儿用的是i、j、k。
• 第二个参数为*operands，表示实际输入的张量列表，其数量必须要和equation中的输入张量对应，即箭头左侧有多少个张量，那么你第二个参数的数量就必须有多少个。同时每个张量的子equation的字符个数要与张量的真实维度对应，即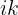本文主要介绍如何使用Pytorch中的爱因斯坦求和（einsum），掌握einsum的基本用法。

equation  中的字符也可以理解为索引，就是输出张量的某个位置的值，是怎么从输入张量中得到的，比如上面矩阵乘法的输出 d 的某个点 d[i, j] 的值是通过 a[i, k] 和 b[i, k] 沿着 k 这个维度做内积得到的。

 

三条规则：

• 规则一：equation 箭头左边，在不同输入之间重复出现的索引表示，把输入张量沿着该维度做乘法操作，比如还是以上面矩阵乘法为例， "ik,kj->ij"，k 在输入中重复出现，所以就是把 a 和 b 沿着 k 这个维度作相乘操作；
• 规则二：只出现在 equation 箭头左边的索引，表示中间计算结果需要在这个维度上求和，即求和索引。（求和索引：只出现在箭头左边的索引，表示中间计算结果需要这个维度上求和之后才能得到输出，比如上面的例子就是 k；）
• 规则三：equation 箭头右边的索引顺序可以是任意的，比如上面的 "ik,kj->ij" 如果写成 "ik,kj->ji"，那么就是返回输出结果的转置，用户只需要定义好索引的顺序，转置操作会在 einsum 内部完成。

# 规则三示例

x = torch.randn(2, 3)
y = torch.randn(3, 4)

m = torch.einsum("ik, kj->ij", x, y)
n = torch.einsum("ik, kj->ji", x, y)
print("a:{} \nb:{}".format(m, n))


# Output：
a:tensor([[-1.0836, -0.2650, -1.7384, -0.5368],
        [ 1.1246, -0.2049,  1.5340,  0.6870]]) 
b:tensor([[-1.0836,  1.1246],
        [-0.2650, -0.2049],
        [-1.7384,  1.5340],
        [-0.5368,  0.6870]])

特殊规则

• equation 也可以不写包括箭头在内的右边部分，那么在这种情况下，输出张量的维度会根据默认规则推导。就是把输入中只出现一次的索引取出来，然后按字母表顺序排列，比如上面的矩阵乘法 "ik,kj->ij" 也可以简化为 "ik,kj"，根据默认规则，输出就是 "ij" 与原来一样；
• equation 中支持 "..." 省略号，用于表示用户并不关心的索引，比如只对一个高维张量的最后两维做转置可以这么写：

t = torch.randn(1, 3, 5, 7, 9)
res = torch.einsum('...ij->...ji', t)
print(res.size())

# Output：
torch.Size([1, 3, 5, 9, 7])

einsum例子

• 提取矩阵对角线元素

# 构造一个tensor a
a = torch.arange(9).reshape(3, 3)   # .reshape(3, 3)等价于.view(3, 3)

print(a)

# 法一：提取矩阵对角线元素
diag1 = torch.einsum('ii->i', a)
print(diag1)

# 法二：torch.diagonal(tensor, offset)：对tensor取对角线元素，offset为偏移量，0为主对角线，1为主对角线下一个对角线
diag2 = torch.diagonal(a, 0)
print(diag2)

# 法三：通过numpy，双重for
out = np.empty((3,), dtype=np.int32)
for i in range(0, 3):
    sum = 0
    for inner in range(0, 1):
        sum += a.numpy()[i, i]
    out[i] = sum
print(out)

• 矩阵转置

a = torch.arange(6).view(2, 3)
print("a: ", a)
a_trans1 = torch.einsum('ij->ji', a)

# torch.transpose(Tensor,dim0,dim1)：transpose()一次只能在两个维度间进行转置
a_trans2 = torch.transpose(a, 0, 1)

print("a_trans1:{}\na_trans2:{}".format(a_trans1, a_trans2))

• permute高维张量转置

# 高维张量转置(两种方法)
b = torch.randn(2, 4, 6, 3, 8)

b_trans1 = torch.einsum('...ij->...ji', b)

b_trans2 = b.permute(0, 1, 2, 4, 3)
print("shape1:\n{}\nshape2:\n{}".format(b_trans1.shape, b_trans2.size()))


# Output：
shape1:
torch.Size([2, 4, 6, 8, 3])
shape2:
torch.Size([2, 4, 6, 8, 3])

• sum求和

a = torch.arange(6).view(2, 3)

# 矩阵所有元素求和
sum1 = torch.einsum('ij->', a)
sum2 = torch.sum(a)
print("a:{}\nsum1:{}, sum2:{}".format(a, sum1, sum2))


# Output：
a:tensor([[0, 1, 2],
        [3, 4, 5]])
sum1:15, sum2:15

• 按列求和

# 矩阵按列求和
a = torch.arange(6).view(2, 3)

sum3 = torch.einsum('ij->j', a)
sum4 = torch.sum(a, dim=0)
print(sum3, sum4)


#Output：
tensor([3, 5, 7]) tensor([3, 5, 7])

---

参考文章：

https://zhuanlan.zhihu.com/p/71639781

一文学会 Pytorch 中的 einsum