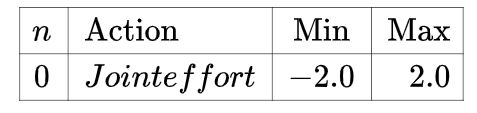【深度强化学习】8. DDPG算法及部分代码解析

【DataWhale打卡】DDPG算法 Deep Deterministric Policy Gradient

视频参考自：https://www.bilibili.com/video/BV1yv411i7xd?p=19

1、思维导图

2. 详解

DDPG是解决连续性控制问题的一个算法，但是和PPO不同，PPO输出是一个策略，是一个概率分布。而DDPG输出的是一个动作。

DDPG是采用的也是Actor-Critic架构，是基于DQN进行改进的。DQN中的action space必须是离散的，所以不能处理连续的动作空间的问题。DDPG在其基础上进行改动，引入了一个Actor Network,让一个网络来的输出来得到连续的动作空间。

对比	AC	DDPG
Actor	输出的是概率分布	输出是动作
Critic	预估V值	预估Q值
更新	带权重梯度更新	梯度上升

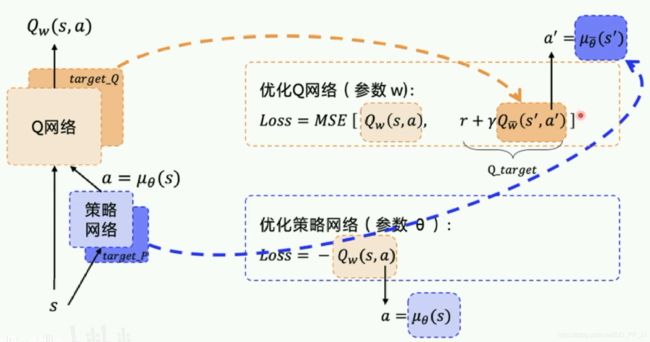
优化Q网络的时候，如果Q-target也在不停的变动，那就会造成更新困难。类似DQN，DDPG也采取了固定网络结构的方法，先冻结target网络，更新参数以后，再把参数赋值到target网络。所以需要的是四个网络：

• actor
• critic
• target actor
• target critic

通过上图可以看出，DDPG(也是一种Actor-Critic方法)，其实也是一种时序差分的方法，结合了基于Value-based和Policy-Based方法。其中Policy是Actor，用于给出动作；价值函数是Critic，评价Actor给出的Action的好坏，产生时序差分信号用于指导价值函数和策略函数的更新。

3. 代码

代码主要看DDPG算法主要几个模块：

3.1 背景

DDPG这里要解决的问题是一个钟摆问题，Pendulum-v0。这个版本的问题中，钟摆以随机位置开始，目标是将其向上摆动，使其保持直立。这是一个连续控制的问题。

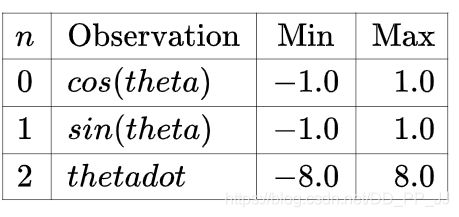
状态表示:

动作空间：

奖励评估：
$$-({\theta }^2+0.1\ast {\theta }_{dt}^2+0.001\ast actio{n}^2)$$
可以看出，目标就是保持零角度，也就是垂直，同时要求旋转速度最小，力度最小。

3.2 Actor

Actor作用是接收状态描述，输出一个action，由于DDPG中的动作空间要求是连续的，所以使用了一个tanh

class Actor(nn.Module):
    def __init__(self, n_obs, n_actions, hidden_size, init_w=3e-3):
        super(Actor, self).__init__()  
        self.linear1 = nn.Linear(n_obs, hidden_size)
        self.linear2 = nn.Linear(hidden_size, hidden_size)
        self.linear3 = nn.Linear(hidden_size, n_actions)
        
        self.linear3.weight.data.uniform_(-init_w, init_w)
        self.linear3.bias.data.uniform_(-init_w, init_w)
        
    def forward(self, x):
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = F.tanh(self.linear3(x))
        return x

实现方面，就是用了几个全连接层来设计的网络，输出的结果是一个连续的值。

3.3 Critic

Critic批评者，在DDPG中，接受来自Actor的一个Action值和当前的状态，输出的是当前状态下，采用Action动作以后得到的关于Q的期望。

class Critic(nn.Module):
    def __init__(self, n_obs, n_actions, hidden_size, init_w=3e-3):
        super(Critic, self).__init__()
        
        self.linear1 = nn.Linear(n_obs + n_actions, hidden_size)
        self.linear2 = nn.Linear(hidden_size, hidden_size)
        self.linear3 = nn.Linear(hidden_size, 1)
        # 随机初始化为较小的值
        self.linear3.weight.data.uniform_(-init_w, init_w)
        self.linear3.bias.data.uniform_(-init_w, init_w)
        
    def forward(self, state, action):
        # 按维数1拼接
        x = torch.cat([state, action], 1)
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = self.linear3(x)
        return x

3.4 Replay Buffer

Replay Buffer就是用来存储一系列等待学习的SARS片段。

class ReplayBuffer:
    def __init__(self, capacity):
        self.capacity = capacity
        self.buffer = []
        self.position = 0
    
    def push(self, state, action, reward, next_state, done):
        if len(self.buffer) < self.capacity:
            self.buffer.append(None)
        self.buffer[self.position] = (state, action, reward, next_state, done)
        self.position = (self.position + 1) % self.capacity
    
    def sample(self, batch_size):
        batch = random.sample(self.buffer, batch_size)
        state_batch, action_batch, reward_batch, next_state_batch, done_batch = map(np.stack, zip(*batch))
        return state_batch, action_batch, reward_batch, next_state_batch, done_batch
    
    def __len__(self):
        return len(self.buffer)

可以设置Replay Buffer的容量，push函数是向buffer中添加一个SARS片段；sample代表从buffer中采样batch size个片段。

3.5 DDPG

DDPG用到了以上的所有对象，包括Critic、Target Critic、Actor、Target Actor、memory。

init函数如下：

def __init__(self, n_states, n_actions, hidden_dim=30, device="cpu", critic_lr=1e-3,
                actor_lr=1e-4, gamma=0.99, soft_tau=1e-2, memory_capacity=100000, batch_size=128):
    self.device = device
    
    self.critic = Critic(n_states, n_actions, hidden_dim).to(device)
    self.actor = Actor(n_states, n_actions, hidden_dim).to(device)

    self.target_critic = Critic(n_states, n_actions, hidden_dim).to(device)
    self.target_actor = Actor(n_states, n_actions, hidden_dim).to(device)

    for target_param, param in zip(self.target_critic.parameters(), self.critic.parameters()):
        target_param.data.copy_(param.data)
    for target_param, param in zip(self.target_actor.parameters(), self.actor.parameters()):
        target_param.data.copy_(param.data)

    self.critic_optimizer = optim.Adam(
        self.critic.parameters(),  lr=critic_lr)
        
    self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=actor_lr)
    
    self.memory = ReplayBuffer(memory_capacity)

    self.batch_size = batch_size
    self.soft_tau = soft_tau
    self.gamma = gamma

其中核心的函数就是update函数：

def update(self):
    if len(self.memory) < self.batch_size:
        return
    state, action, reward, next_state, done = self.memory.sample(
        self.batch_size)
    # 将所有变量转为张量
    state = torch.FloatTensor(state).to(self.device)
    next_state = torch.FloatTensor(next_state).to(self.device)
    action = torch.FloatTensor(action).to(self.device)
    reward = torch.FloatTensor(reward).unsqueeze(1).to(self.device)
    done = torch.FloatTensor(np.float32(done)).unsqueeze(1).to(self.device)
    # 注意critic将(s_t,a)作为输入
    policy_loss = self.critic(state, self.actor(state))
    
    policy_loss = -policy_loss.mean()

    next_action = self.target_actor(next_state)
    target_value = self.target_critic(next_state, next_action.detach())
    expected_value = reward + (1.0 - done) * self.gamma * target_value
    expected_value = torch.clamp(expected_value, -np.inf, np.inf)

    value = self.critic(state, action)
    value_loss = nn.MSELoss()(value, expected_value.detach())
    
    self.actor_optimizer.zero_grad()
    policy_loss.backward()
    self.actor_optimizer.step()

    self.critic_optimizer.zero_grad()
    value_loss.backward()
    self.critic_optimizer.step()
    for target_param, param in zip(self.target_critic.parameters(), self.critic.parameters()):
        target_param.data.copy_(
            target_param.data * (1.0 - self.soft_tau) +
            param.data * self.soft_tau
        )
    for target_param, param in zip(self.target_actor.parameters(), self.actor.parameters()):
        target_param.data.copy_(
            target_param.data * (1.0 - self.soft_tau) +
            param.data * self.soft_tau
        )

整体流程如下：

• 从memory中采样一个batch的数据。
• policy_loss = self.critic(state, self.actor(state))
  • 将state放到actor对象得到action
  • 将state,action放到critic对象得到policy loss

next_action = self.target_actor(next_state)
target_value = self.target_critic(next_state, next_action.detach())

• 然后target actor和target critic也按照以上过程得到target value
• 根据target value 计算expected value:

$$r+\gamma Q$$

实现如下：

expected_value = reward + (1.0 - done) * self.gamma * target_value
expected_value = torch.clamp(expected_value, -np.inf, np.inf)

如果done为1，代表已经结束了，也就不需要这个系数了。第二行对expected value进行了数值上的限制。

• 接下来计算根据数据集中action得到的value值。

value = self.critic(state, action)

• 计算优化Q网络的loss, 采用的是MSEloss

value_loss = nn.MSELoss()(value, expected_value.detach())

对比下图：

• 对policy loss和value loss进行梯度回传，更新训练参数。

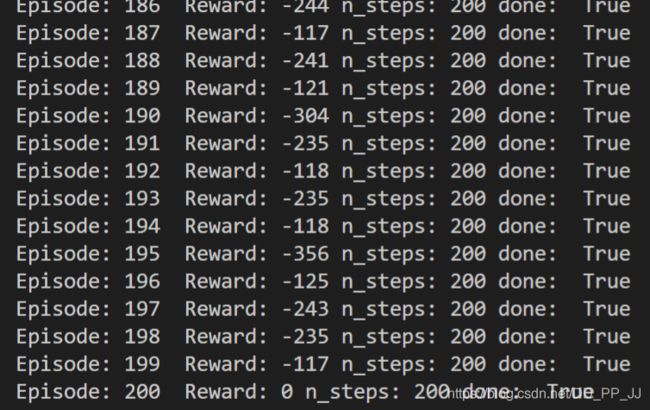
训练结果如下：

4. 参考文献

代码部分全部来自于johnjim的实现，感谢。

https://www.jianshu.com/p/af3a7853268f

https://datawhalechina.github.io/leedeeprl-notes/#/chapter12/project3

https://www.bilibili.com/video/BV1yv411i7xd?p=19