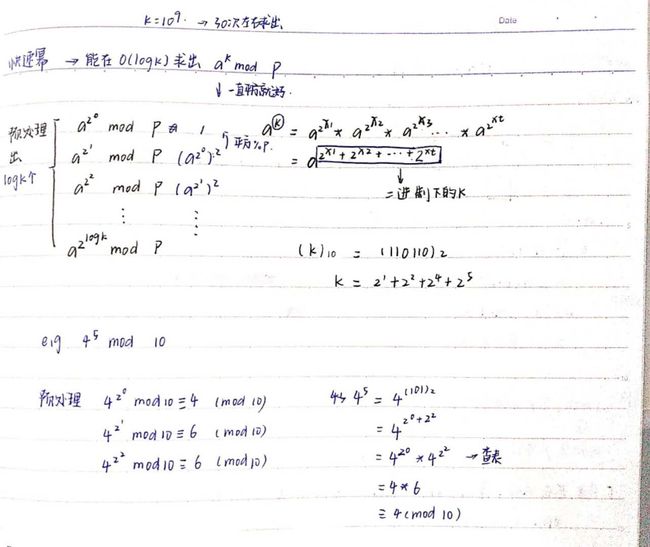蒟蒻de数学笔记(持续更新)
数论
我做了好久啊 总结题解什么的太耗时间了。。
后面有手写笔记(关注内容,别关注我的字就好qwq)
质数
试除法判定质数
bool is_prime(int x)
{
if(x<2) return 0;
for(int i=2;i<=x/i;i++) //i<=x/i等同于 i*i<=x 等同于i<=sqrt(x)
if(x%i==0) return 0;
return 1;
}
分解质因数
1.根据算术基本定理,不考虑排列顺序的情况下,每个正整数都能 够以唯一的方式表示成它的质因数的乘积。
n=p1^a1 * p2^a2 *p3a3…pnan
2.性质:n中最多只含有一个大于sqrt(n)的因子
反证法证明:如果有两个大于sqrt(n)的因子,那么相乘会大于n,矛盾 证毕。
我们发现最多只有一个大于sqrt(n)的因子,可对代码进行优化 先考虑比sqrt(n)小的
3.如果最后n还是>1,说明这就是大于sqrt(n)的唯一质因子
for(int i=2;i<=x/i;i++)
{
if(x%i==0)
{
int cnt=0;
while(1)
{
if(x%i!=0) break;
x/=i;
cnt++;
}
cout<<i<<" "<<cnt<<endl;
}
}
if(x>1) cout<<x<<" "<<1<<endl; //唯一大于sqrt(n)的质因子
筛质数
通常有两种常用筛法 (埃氏筛和线性筛——>也叫做欧拉筛) 相比于埃氏筛 线性筛 每个合数i*p只会被它的最小质因子筛一遍 O(n) 故得名线性筛,时间复杂度更优
为什么呢?
i * p只会被最小的质因子筛掉,每个数只有一个最小质因子,所以每个数只会被筛一次
当i%pj==0时,pj一定是i最小质因子,也一定是pj∗i的最小质因子
当i%pj!=0时, pj一定小于i的所有质因子,pj也一定是pj∗i的最小质因子
void xxs()//求1~n的所有素数
{
for(int i=2;i<=n;i++)
{
if(!vis[i]) prime[++cnt]=i;
for(int j=1;prime[j]<=n/i;j++)
{
vis[prime[j]*i]=1;//把它筛掉
if(i%prime[j]==0) break;
}
}
}
约数
以下是关于约数的应用
试除法求约数
void find(int x) //找x的所有约数
{
memset(p,0,sizeof(p));
cnt=0;
for(int i=1;i<=x/i;i++)
{
if(x%i==0)
{
p[++cnt]=i;
if(i!=x/i) p[++cnt]=x/i; //这里要特判一下平方数
}
}
sort(p+1,p+1+cnt);
for(int i=1;i<=cnt;i++) cout<<p[i]<<" ";
cout<<endl;
}
约数个数
/*
约数个数定理
由算术基本定理可唯一分解成 N=p1^c1+p2^c2+...+pm^cm
对于每个数pi都有0~ci 共ci+1中指数的选法
pi都是质数) N的正约数个数为 ans=(c1+1)*(c2+1)*...*(cm+1)
这里求所有数乘积的约数个数之和 直接乘在一起会爆掉
考虑分别把每个质因子的指数累加 然后把这些质因子的指数+1再相乘
可以用unordered_map
*/
#include约数之和
#include最大公约数
(证明可能不严谨的地方请大佬指出)
int gcd(int a,int b)
{
return b? gcd(b,a%b) :a;
}
欧拉函数
phi(n)=1~n中与n互质的数的个数
下面是它的公式 和 一个简单的小栗子
证明如下:
int phi(int x)
{
int res=x;
for(int i=2;i<=x/i;i++)
{
if(x%i==0)//i是x的质因子
{
res=res/i*(i-1);
while(x%i==0) x/=i;
}
}
if(x>1) res=res/x*(x-1); //等同于res*(1-1/x) 不过这样没有小数
return res;
}
但是如果要求1~n中每个数的欧拉函数 一个一个求就太慢了 于是我们考虑用线性筛来求
或者你懒(不想看这一堆证明的话,可以康康结论)
void get_ola(int n)
{
phi[1]=1;
for(int i=2;i<=n;i++)
{
if(!vis[i]) primes[++cnt]=i, phi[i]=i-1;//是质数
for(int j=1;primes[j]<=n/i;j++)//j++写成i++了 调了好久.....
{
int pj=primes[j];
vis[pj*i]=1;
if(i%pj==0) //pj是i的最小质因子,所以也是pj*i 的最小质因子 做完就可以break了
{
phi[pj*i]=phi[i]*pj;
break;
}
if(i%pj!=0) phi[pj*i]=phi[i]*(pj-1);
}
}
}
int main()
{
for(int i=1;i<=n;i++) res+=phi[i];//求1~n中所有欧拉函数的和 你也可以根据题目灵活变通
}
欧拉定理
公式
栗子
证明(欧拉定理 --> 为后面的费马小定理证明带来了极大的便利 -->帮助我们求逆元)
快速幂
ll qmi(ll a,ll b,ll p)// return a^b % p
{
ll res=1;
while(b)
{
if(b&1) res=(res*a)%p;
b>>=1;
a=(a*a)%p;
}
return res;
}
逆元
(蒟蒻懵了好久 枯了)
首先 为什么要逆元这个(huo hai cang sheng 的玩意呢(雾 )
就是说+ - * 都行的东西就/不行 所以要用乘法代替除法来实现一些除法小可怜做不了的东西
我们可以 用快速幂来求(下面是证明)
ll qmi(ll a,ll k,ll p)
{
ll res=1;
while(k)
{
if(k&1) res=res*a%p;
k>>=1;
a=a*a%p;
}
return res;
}
int main()
{
cin>>n;
while(n--)
{
ll a,p;
cin>>a>>p;
if(a%p==0) cout<<"impossible"<<endl;//不互质 无逆元
else cout<<qmi(a,p-2,p)<<endl;
}
return 0;
}