冲刺大厂每日算法&面试题,动态规划21天——第十四天
目录标题
- 导读
- 21天动态规划入门
- 面试题
- 点击直接资料领取
导读
![]()
肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。我们先来搞一下让大家最头疼的一类算法题,动态规划我们将进行为时21天的养成计划。还在等什么快来一起肥学进行动态规划21天挑战吧!!
21天动态规划入门
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j]
是所有满足下述条件的元素 mat[r][c] 的和:i - k <= r <= i + k, j - k <= c <= j + k 且 (r, c) 在矩阵内。
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出:[[45,45,45],[45,45,45],[45,45,45]]
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int n=mat.length,m=mat[0].length;
int[][] dp=new int[n+1][m+1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dp[i][j]=dp[i-1][j]+dp[i][j-1]+mat[i-1][j-1]-dp[i-1][j-1];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int x1=i-k,y1=j-k,x2=i+k,y2=j+k;
if(x1<1) x1=1;
if(y1<1) y1=1;
if(x2>n) x2=n;
if(y2>m) y2=m;
mat[i-1][j-1]=dp[x2][y2]+dp[x1-1][y1-1]-dp[x1-1][y2]-dp[x2][y1-1];
}
}
return mat;
}
}
给定一个二维矩阵 matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) ,右下角 为 (row2, col2) 。 实现
NumMatrix 类:NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化 int sumRegion(int row1,
int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2)
所描述的子矩阵的元素 总和 。
示例 1:
输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]
解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
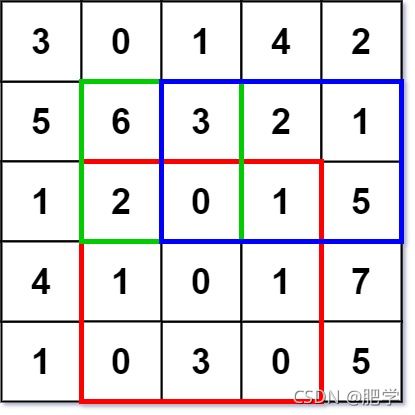
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-105 <= matrix[i][j] <= 105
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 104 次 sumRegion 方法
具体实现方面,创建 mm 行 n+1n+1 列的二维数组 \textit{
sums}sums,其中 mm 和 nn 分别是矩阵 \textit{
matrix}matrix 的行数和列数,\textit{
sums}[i]sums[i] 为 \textit{
matrix}[i]matrix[i] 的前缀和数组。将 \textit{
sums}sums 的列数设为 n+1n+1 的目的是为了方便计算每一行的子数组和,不需要对 \textit{
col}_1=0col 1 =0 的情况特殊处理。
class NumMatrix {
int[][] sums;
public NumMatrix(int[][] matrix) {
int m = matrix.length;
if (m > 0) {
int n = matrix[0].length;
sums = new int[m][n + 1];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sums[i][j + 1] = sums[i][j] + matrix[i][j];
}
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sum = 0;
for (int i = row1; i <= row2; i++) {
sum += sums[i][col2 + 1] - sums[i][col1];
}
return sum;
}
}
面试题
介绍⼀下,什么是Hashmap?
参考回答:
HashMap 是⼀个散列表,它存储的内容是键值对(key-value)映射。
HashMap 继承于AbstractMap,实现了Map、Cloneable、java.io.Serializable接⼝。
HashMap 的实现不是同步的,这意味着它不是线程安全的。它的key、value都可以为null。此
外,HashMap中的映射不是有序的。
HashMap 的实例有两个参数影响其性能:“初始容量” 和 “加载因⼦”。容量 是哈希表中桶的
数量,初始容量 只是哈希表在创建时的容量。加载因⼦ 是哈希表在其容量⾃动增加之前可以
达到多满的⼀种尺度。当哈希表中的条⽬数超出了加载因⼦与当前容量的乘积时,则要对该哈
希表进⾏ rehash 操作(即重建内部数据结构),从⽽哈希表将具有⼤约两倍的桶数。
通常,默认加载因⼦是 0.75, 这是在时间和空间成本上寻求⼀种折衷。加载因⼦过⾼虽然减少
了空间开销,但同时也增加了查询成本(在⼤多数 HashMap 类的操作中,包
括 get 和 put 操作,都反映了这⼀点)。在设置初始容量时应该考虑到映射中所需的条⽬数
及其加载因⼦,以便最⼤限度地减少 rehash 操作次数。如果初始容量⼤于最⼤条⽬数除以加
载因⼦,则不会发⽣ rehash 操作。
hashmap共有4个构造函数:
// 默认构造函数。HashMap()
// 指定“容量⼤⼩”的构造函数
HashMap(int capacity)
// 指定“容量⼤⼩”和“加载因⼦”的构造函数
HashMap(int capacity, float loadFactor)
// 包含“⼦Map”的构造函数
HashMap(Map map)
特别介绍
小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶
python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章,可以让你快乐学python练手项目专栏
另外想学JavaWeb进厂的同学可以看看这个专栏:传送们
这是个面试和考研的算法练习我们一起加油上岸之路
点击直接资料领取
这里有python,Java学习资料还有有有趣好玩的编程项目,更有难寻的各种资源。反正看看也不亏。