推荐系统7——利用上下文信息进行推荐
在之前我也看了很多人写的推荐系统的博客,理论的、算法的都有,多是个人的理解和感悟,虽然很深刻,但是对于自己而言还是不成系统,于是我参考大牛项亮编著的《推荐系统实践》将该领域知识系统整理一遍,与大家一起学习。
本系列对应的代码请查看https://github.com/wangyuyunmu/Recommended-system-practice
前面总结了:
基于用户行为数据的推荐方法——协同过滤、隐语义、图模型;
冷启动——基于物品内容、用户注册信息等;
基于标签的推荐方法;
本篇总结利用上下文信息推荐方法。
目录
- 1,时间上下文信息
-
- 1.1,时间效应简介
- 1.2,系统的时间特性分析
- 1.3,推荐系统的实时性
- 1.4,推荐算法的时间多样性
-
- 1.4.1 如何提高推荐系统的多样性
- 1.5,时间上下文推荐算法
-
- 1.5.1 最近热门
- 1.5.2 时间上下相关的itemCF
- 1.5.3 时间上下相关的userCF算法
- 1.5.4 时间段图模型
- 1.6,离线实验
- 2,地点上下文信息
之前提到的推荐系统算法主要集中研究了如何联系用户兴趣和物品,将最符合用户兴趣的物品推荐给用户,但这些算法都忽略了一点,就是用户所处的上下文(context)。这些上下文包括用户访问推荐系统的时间、地点、心情等,对于提高推荐系统的推荐系统是非常重要的。
本文我们主要讨论时间上下文,讨论如何将时间信息和地点信息建模到推荐算法中,从而让推荐系统能够准确预测用户在某个特定时刻的兴趣。
1,时间上下文信息
1.1,时间效应简介
时间是一种重要的上下文信息,对用户兴趣有着深入而广泛的影响。一般认为,时间信息对用户兴趣的影响表现在以下几个方面:
1)用户兴趣是变化的。比如随着年龄的增长,兴趣不同。
2)物品也是有生命周期的。比如新闻周期短,电影的周期长。
3)季节效应。不同季节有不同的喜好。
1.2,系统的时间特性分析
在给定数据集后,通过统计如下信息研究系统的时间特性。
1)数据集每天独立用户数的增长情况。 判断系统属于快速增长期、平稳期还是衰落期。
2)系统的物品变化情况。 不同系统物品的生命周期不同。
3)用户访问情况。 评估用户的活跃度,可以统计用户的平均活跃天数、统计相隔T天系统的用户重合度。
1.3,推荐系统的实时性
实现推荐系统的实时性除了对用户行为的存取有实时性要求,还要求推荐算法本身具有实时性,而推荐算法本身的实时性意味着。
1)实时推荐系统不能每天都给所有用户离线计算推荐结果,然后在线展示昨天计算出来的结果。所以,要求在每个用户访问推荐系统时,都根据用户这个时间点前的行为实时计算推荐列表。
2)推荐算法需要平衡考虑用户的近期行为和长期行为,即要让推荐列表反应出用户近期行为所体现的兴趣变化,又不能让推荐列表完全受用户近期行为的影响,要保证推荐列表对用户兴趣预测的延续性。
1.4,推荐算法的时间多样性
很多推荐系统的研究人员经常遇到一个问题,就是每天给用户的推荐结果都差不多,没有什么变化。推荐系统每天推荐结果的变化程度被定义为推荐系统的时间多样性。时间多样性高的推荐系统中用户会经常看到不同的推荐结果。
那么推荐系统的时间多样性和用户满意度之间是否存在关系呢?
1)纯粹的随机推荐虽然具有最高的时间多样性,但不能保证推荐的精度。用户满意度低。
2)没有时间多样性,从而造成用户满意度随着时间不断下降。
所以要做到在不损失精度的情况下,提高推荐结果的时间多样性。
1.4.1 如何提高推荐系统的多样性
提高推荐结果的时间多样性需要分两步解决:首先,需要保证推荐系统能够在用户有了新的行为后及时调整推荐结果,使推荐结果满足用户最近的兴趣;其次,需要保证推荐系统在用户没有新的行为时也能够经常变化一下结果,具有一定的时间多样性。
第一步是推荐系统的试试性角度分析,第二步,如何能经常产生一些变化呢?
1)在生成推荐结果的时候加入一些随机性。比如从top20中,随机挑选10个。
2)对用户推荐时,对用户前几天看过的物品进行适当降权。
3)每天使用不同的推荐方法。
1.5,时间上下文推荐算法
1.5.1 最近热门
在没有时间信息的数据集中,给用户推荐历史上热门的物品。在获得用户行为时间信息后,进行简单的加权。
n i ( T ) = ∑ ( u , i , t ) ∈ t r a i n , t < T 1 1 + α ( T − t ) n_i(T)=\sum_{(u,i,t)\in train,t
1.5.2 时间上下相关的itemCF
物品相似度的计算过程中添加时间相关权值衰减。
s i m ( i , j ) = ∑ u ∈ N ( i ) ∩ N ( j ) f ( ∣ t u i − t u j ∣ ) ∣ N ( i ) ∣ ∣ N ( j ) ∣ sim(i,j)=\frac{\sum_{u \in N(i) \cap N(j)}f(|t_{ui}-t_{uj}|)}{\sqrt{|N(i)||N(j)|}} sim(i,j)=∣N(i)∣∣N(j)∣∑u∈N(i)∩N(j)f(∣tui−tuj∣) f ( ∣ t u i − t u j ∣ ) = 1 1 + α ∣ t u i − t u j ∣ f(|t_{ui}-t_{uj}|)=\frac{1}{1+\alpha |t_{ui}-t_{uj}|} f(∣tui−tuj∣)=1+α∣tui−tuj∣1函数的含义是,用户对物品i和物品j产生行为的时间越远,则f越小。
除了考虑时间信息对相关表的影响,我们也应该考虑时间信息对预测公式的影响。一般来说,用户现在的行为应该和用户最近的行为关系更大。
p ( u , i ) = ∑ j ∈ N ( u ) ∩ S ( i , k ) s i m ( i , j ) 1 1 + β ∣ t 0 − t u j ∣ p(u,i)=\sum_{j\in N(u)\cap S(i,k)}sim(i,j)\frac{1}{1+\beta|t_0-t_{uj}|} p(u,i)=j∈N(u)∩S(i,k)∑sim(i,j)1+β∣t0−tuj∣1
1.5.3 时间上下相关的userCF算法
用户u和用户v对物品i产生行为的时间越远,那么这两个用户的兴趣相似度就会越小。
w u v = ∑ i ∈ N ( u ) ∩ N ( j ) 1 1 + α ∣ t u i − t v i ∣ ( ∣ N ( u ) ∣ ∪ ∣ N ( v ) ∣ ) w_{uv}=\frac{\sum_{i\in N(u)\cap N(j)}\frac{1}{1+\alpha |t_{ui}-t_{vi}|}}{\sqrt(|N(u)|\cup |N(v)|)} wuv=(∣N(u)∣∪∣N(v)∣)∑i∈N(u)∩N(j)1+α∣tui−tvi∣1在得到用户相似度后,UserCF通过如下公式预测用户对物品的兴趣,和用户u兴趣相似用户的最近兴趣。
p ( u , i ) = ∑ v ∈ S ( u , K ) w u v r v i 1 1 + α ( t 0 − t v t ) p(u,i)=\sum_{v\in{S(u,K)}}w_{uv}r_{vi}\frac{1}{1+\alpha(t_0-t_{vt})} p(u,i)=v∈S(u,K)∑wuvrvi1+α(t0−tvt)1
如果用户v对物品i产生过行为,那么r =1 ,否则 r =0.
1.5.4 时间段图模型
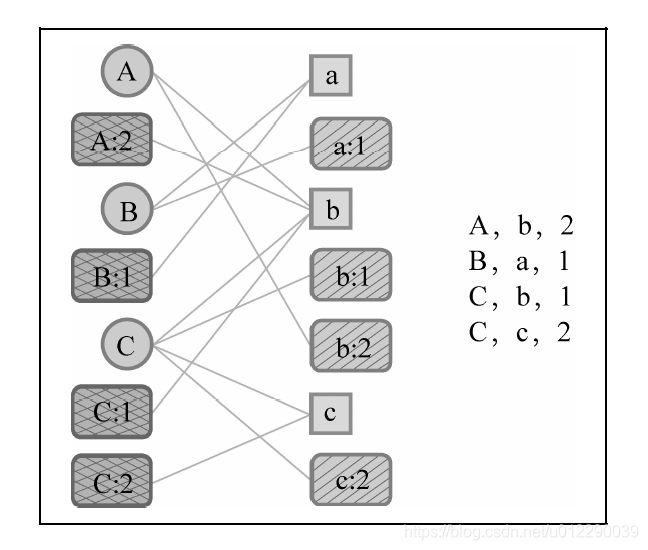
时间段图模型G(U, S u S_u Su,I, S I S_I SI,E,w, σ \sigma σ)也是一个二分图。U是用户节点集合, S u S_u Su 是用户时间段节点集合。一个用户时间段节点 v u t ∈ S u v_{ut} \in{S_u} vut∈Su 会和用户u在时刻t喜欢的物品通过边相连。I是物品节点集合, S I S_I SI 是物品时间段节点集合。一个物品时间段节点 v i t ∈ S I v_{it}\in{S_I} vit∈SI 会和所有在时刻t喜欢物品i的用户通过边相连。E是边集合,w(e)定义了边的权重,σ (e)定义了顶点的权重。
用户A在时刻2对物品b产生了行为。因此,时间段图模型会首先创建4个顶点,即用户顶点A、用户时间段顶点A:2、物品顶点b、物品时间段顶点b:2。然后,图中会增加3条边,即(A, b)、(A:2, b)、(A, b:2)。这里不再增加(A:2, b:2)这条边,一方面是因为增加这条边后不会对结果有所改进,另一方面则是因为增加一条边会增加图的空间复杂度和图上算法的时间复杂度。
Personalrank算法可以实现推荐过程,但是时间复杂度比较高。下面介绍路径融合算法方法。
路径融合算法
一般来说,图上两个相关性比较高的顶点一般具有如下特征:
1)两个顶点之间有很多路径相连;
2)两个顶点之间的路径比较短;
3)两个顶点之间的路径不经过出度比较大的顶点。
从这3条原则出发,路径融合算法首先提取出两个顶点之间长度小于一个阈值的所有路径,
然后根据每条路径经过的顶点给每条路径赋予一定的权重,最后将两个顶点之间所有路径的权重之和作为两个顶点的相关度。
根据定义得出某条路径的权重:
Γ ( P ) = σ ( v n ) ∏ i = 1 n − 1 σ ( v i ) w ( v i , v i + 1 ) ∣ o u t ( v i ) ∣ ρ \Gamma{(P)}=\sigma(v_n)\prod_{i=1}^{n-1}\frac{\sigma(v_i)w(v_i,v_{i+1})}{|out(v_i)|^{\rho}} Γ(P)=σ(vn)i=1∏n−1∣out(vi)∣ρσ(vi)w(vi,vi+1)满足第2、3个条件:out越大,权值越小,路径n越长,连乘的结果越小。
那么这两个顶点之间的相关度可以定义为:
d ( v , v ˊ ) = ∑ P ∈ P ( v , v ˊ , K ) Γ ( P ) d(v,\acute{v})=\sum_{P\in{P(v,\acute{v},K)}}\Gamma(P) d(v,vˊ)=P∈P(v,vˊ,K)∑Γ(P)两点之间相连的路径越多,相关度越高。
对于时间段图模型,所有边的权重都定义为1,顶点权重 σ \sigma σ
σ ( v ) = { 1 − α v ∈ U α v ∈ S u 1 − β v ∈ I β v ∈ S I \sigma(v)= \begin{cases} 1-\alpha&{v\in{U}}\\ \alpha&{v\in{S_u}}\\ 1-\beta&{v\in{I}}\\ \beta&{v\in{S_I}} \end{cases} σ(v)=⎩⎪⎪⎪⎨⎪⎪⎪⎧1−αα1−ββv∈Uv∈Suv∈Iv∈SI
1.6,离线实验
1)Pop 给用户推荐当天最热门的物品。
2)TItemCF 融合时间信息的ItemCF算法。
3)TUserCF 融合时间信息的UserCF算法。
4)ItemCF 不考虑时间信息的ItemCF算法。
5)UserCF 不考虑时间信息的UserCF算法。
6)SGM 时间段图模型。
7)USGM 物品时间节点权重为0的时间段图模型。
8)ISGM 用户时间节点权重为0的时间段图模型。
选择delicious数据集,对比’www.nytimes.com’与’en.wikipedia.org’两个网站的访问数据。数据提取形式user:item+time
def loadData(self):
bookmarks = [f.strip() for f in codecs.open(self.bookmark_path, 'r', encoding="ISO-8859-1").readlines()][1:]
# 将不同网站对应的item与时间保存下来
site_ids = {
}
for b in bookmarks:
b = b.split('\t')
if b[-1] not in site_ids:
site_ids[b[-1]] = set()
site_ids[b[-1]].add(b[0])
user_bookmarks = [f.strip() for f in
codecs.open(self.user_bookmark_path, 'r', encoding="ISO-8859-1").readlines()][1:]
data = {
}
cnt = 0
# 选择和收集对应的url的user:item+time数据,并按照时间对每个user进行排序
for ub in user_bookmarks:
ub = ub.split('\t')
if self.site is None or (self.site in site_ids and ub[1] in site_ids[self.site]):
if ub[0] not in data:
data[ub[0]] = set()
data[ub[0]].add((ub[1], int(ub[3][:-3])))
cnt += 1
self.data = {
k: list(sorted(list(data[k]), key=lambda x: x[1], reverse=True)) for k in data}
Pop 给用户推荐当天最热门的物品。这里的主要区别是时间加权。
item_score = {
}
for user in train:
for item, t in train[user]:
if item not in item_score:
item_score[item] = 0
item_score[item] += 1.0 / (alpha * (t0 - t))
item_score = list(sorted(item_score.items(), key=lambda x: x[1], reverse=True))
TItemCF 融合时间信息的ItemCF算法。同理。
# 计算物品相似度矩阵
sim = {
}
num = {
}
for user in train:
items = train[user]
for i in range(len(items)):
u, t1 = items[i]
if u not in num:
num[u] = 0
num[u] += 1
if u not in sim:
sim[u] = {
}
for j in range(len(items)):
if j == i: continue
v, t2 = items[j]
if v not in sim[u]:
sim[u][v] = 0
sim[u][v] += 1.0 / (alpha * (abs(t1 - t2) + 1))
for u in sim:
for v in sim[u]:
sim[u][v] /= math.sqrt(num[u] * num[v])
TUserCF 融合时间信息的UserCF算法。同理。
# 计算item->user的倒排索引
item_users = {
}
for user in train:
for item, t in train[user]:
if item not in item_users:
item_users[item] = []
item_users[item].append((user, t))
# 计算用户相似度矩阵
sim = {
}
num = {
}
for item in item_users:
users = item_users[item]
for i in range(len(users)):
u, t1 = users[i]
if u not in num:
num[u] = 0
num[u] += 1
if u not in sim:
sim[u] = {
}
for j in range(len(users)):
if j == i: continue
v, t2 = users[j]
if v not in sim[u]:
sim[u][v] = 0
sim[u][v] += 1.0 / (alpha * (abs(t1 - t2) + 1))
for u in sim:
for v in sim[u]:
sim[u][v] /= math.sqrt(num[u] * num[v])
测试结果:
#Popular
Result (site=www.nytimes.com, K=0, N=10): {
'Precision': 0.16, 'Recall': 1.58}
Result (site=en.wikipedia.org, K=0, N=10): {
'Precision': 0.0, 'Recall': 0.0}
#TitemCF
Result (site=www.nytimes.com, K=10, N=10): {
'Precision': 1.81, 'Recall': 1.81}
Result (site=en.wikipedia.org, K=10, N=10): {
'Precision': 0.36, 'Recall': 0.25}
#TuserCF
Result (site=www.nytimes.com, K=10, N=10): {
'Precision': 2.68, 'Recall': 1.81}
Result (site=en.wikipedia.org, K=10, N=10): {
'Precision': 0.87, 'Recall': 0.25}
#itemCF
Result (site=www.nytimes.com, K=10, N=10): {
'Precision': 1.81, 'Recall': 1.81}
Result (site=en.wikipedia.org, K=10, N=10): {
'Precision': 0.36, 'Recall': 0.25}
#userCF
Result (site=www.nytimes.com, K=10, N=10): {
'Precision': 3.02, 'Recall': 2.03}
Result (site=en.wikipedia.org, K=10, N=10): {
'Precision': 0.87, 'Recall': 0.25}
本篇文章测试结果与书中有较大区别,个人认为其中很大一部分原因是数据集问题,本文下载的数据集版本1.0,比如,其中nytimes的users只有几百,而书中所用数据集4947。
不同的数据集对应算法的性能也不一样,有的数据集对于用户兴趣的个性化不是特别明显,时效性强,比如新闻类,每天的热门物品就可以吸引绝大多数用户的眼球。而有的数据集需要重点分析用户的个性化需求。
2,地点上下文信息
用户兴趣和地点比较相关的两种特征:
1)兴趣本地化: 不同地方的用户兴趣存在着很大的差别。不同国家和地区用户的兴趣存在着一定的差异性
2)活动本地化: 一个用户往往在附近的地区活动。通过分析Foursqure的数据,研究人员发现45%的用户其活动范围半径不超过10英里,而75%的用户活动半径不超过50英里。因此,在基于位置的推荐中我们需要考虑推荐地点和用户当前地点的距离,不能给用户推荐太远的地方。