背景
自己手头有一堆经过初始配准后的三维散乱点云,经过粗配后,全部点云基本统一在了同一个坐标系下,如图1和图2所示。为了获取更好的全局结果,需要对粗配后的点云进行全局配准优化。
 图1 点云底面 图1 点云底面 |
 图2 局部细节 图2 局部细节 |
上述点云是基于pcl进行显示,不同的颜色代表不同的点云块,从图1可以明显看出,全局点云"融合"(其实并未融合,只是全部加载显示),效果较差,从图2可以看出,针对[耳朵]部分出现较大错位。
因为自己之前对G2O多多少少有一点了解,但是也并没有进行过多深入的研究。知道G2O可以用来解决全局优化问题,正好和自己要求解的问题非常非常相似。
因此,便毅然决然的选择使用G2O来针对自己的问题构建解决方案。
G2O的进一步了解
G2O是将非线性优化和图论相结合的产物,大多时候用于解决slam后端优化问题,其自身携带的例子大多也与slam有关。g2o中所谓的图,就是一堆节点和边按照一定的关系链接而成。其中,节点是要优化的目标,边是各个优化目标之间的关系(也称其误差项,在这里自己更喜欢称为 【关系】)。
基于CMake + VS2017 完成G2O库的安装,安装过程没有做详细记录,基本百度能够解决。
安装完g2o后,按照习惯去翻看其自身源码中所携带的example,以便寻找灵感,在example目录中一眼便看中了【gicp_demo】。
G2O--gicp_demo
g2o的使用方法基本就是:
- 声明一个优化器;
- 选择求解方法;
- 构造图--顶点和边的关系;
- 优化处理。
初次看到g2o的gicp时,自认为“该gicp方法是 全局(global)的”,然而事实并非如此,事实上,其甚至不能称为是一个完整的icp问题
(关于上述红色字体的表示,目前仅仅是个人理解,或许有错误,也请多多留言指正,一起交流学习)
我们知道,ICP求解是一个迭代计算过程,经典ICP求解的主要步骤为:
- 输入两片点云AB,求解对应点对(三维模型至少3个不共线的点);
- 基于对应点对,构造A到B的变换矩阵M;
- 将M作用于A,得到A*,并用A*代替A;
- 迭代终止条件(迭代次数或者最小误差度量);
- 重复步骤1--3,直到满足步骤4,终止。
- 输出变换矩阵M。
但是细看g2o的gicp_demo,其流程并不如经典ICP求解过程一样,而更像一个ICP中步骤2的求解问题。
再来深入看看g2o中给出的gicp_demo。
拆解gicp_demo
首先还是直接先把g2o官方例子贴出来吧(虽然非常讨厌直接贴别人代码),便于说明。
在该Demo中,g2o首先声明并设置了优化器optimizer,并制作了包含1000个点的集合true_points作为源点云。
其次,为图添加了两个节点并设置节点ID。这里的节点类型为VertexSE3( class G2O_TYPES_SLAM3D_API VertexSE3 : public BaseVertex<6, Isometry3>),也是主要的优化目标。依据节点添加到图中的顺序,将第一次添加的节点视为固定视角;vc->setEstimate(cam);该代码段告诉我们,真正求解的结果是存储在Eigen::Isometry3d类型的相机位姿(本质上是一个矩阵),这里cam参数的类型是Eigen::Isometry3d;这一步其实只是声明了两个空节点,节点参数只是单位Eigen::Isometry3d。
再次,为图添加了1000条边。在此过程中,首先根据节点id获取边所需要链接的两个顶点(节点),vp0和vp1,并基于true_points "制作" 了包含噪声的两个三维点pt0和 pt1(这一步其实已经默认pt0和 pt1为对应点对);然后 声明了一个Edge_V_V_GICP类型的图边结构,该边是一个g2o的二元边(class G2O_TYPES_ICP_API Edge_V_V_GICP : public BaseBinaryEdge<3, EdgeGICP, VertexSE3, VertexSE3>),该二元边分别链接vp0和vp1;g2o还提供了EdgeGICP类型作为观测值,EdgeGICP类型可以存放对应点对。在该步骤中,一定要非常注意节点和三维坐标点的所属--对应关系。至此,基本能够将所有信息放入g2o的图中,该步骤主要关心的在于如何将自己的三维点对放入到g2o图中。
最后,初始化图关系并进行了N次迭代优化,每个节点的优化结果存储在optimizer.vertices()返回值类型的哈希表中,该哈希表中:键--对应节点id,值--对应节点,这里为VertexSE3类型,从VertexSE3获得的Eigen::Isometry3d类型是我们真正关心的结果数据。
该示例应该构建了如下一张超图,其中图有两个图节点,n1为固定节点,n2为变动的节点,节点之间有1000条边,每条边链接一对对应点,针对ICP问题,对应点中的固定点挂接图节点n1,变动的点挂接图节点n2:

| 节点--边 |
void icp() {
double euc_noise = 0.01; // noise in position, m
//声明优化器
SparseOptimizer optimizer;
//是否打印详细信息
optimizer.setVerbose(false);
// variable-size block solver
//设定一个求解方法
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(
g2o::make_unique(g2o::make_unique>()));
/*g2o::OptimizationAlgorithmGaussNewton *solver = new g2o::OptimizationAlgorithmGaussNewton(
g2o::make_unique(g2o::make_unique>()));*/
//设定优化器使用的优化方法
optimizer.setAlgorithm(solver);
//随机点坐标
vector true_points;
for (size_t i = 0; i < 1000; ++i)
{
//这里从均匀分布中采样了一组数字
true_points.push_back(Vector3d((g2o::Sampler::uniformRand(0., 1.) - 0.5) * 3,
g2o::Sampler::uniformRand(0., 1.) - 0.5,
g2o::Sampler::uniformRand(0., 1.) + 10));
}
// set up two poses
//猜测: 设定两个相机位姿
int vertex_id = 0;
for (size_t i = 0; i < 2; ++i)
{
// set up rotation and translation for this node
//平移向量
Vector3d t(0, 0, i);
//四元数旋转
Quaterniond q;
q.setIdentity();
//李群(特殊欧拉群,包含旋转和平移,自己感觉和4*4矩阵类似)
Eigen::Isometry3d cam; // camera pose
cam = q;
//返回平移向量的可写表达式
cam.translation() = t;
// set up node
//李群。这里作为节点,作为优化变量
VertexSE3 *vc = new VertexSE3();
//设置顶点的估计值
vc->setEstimate(cam);
//设置该节点在 图 中的id,以便追踪
vc->setId(vertex_id); // vertex id
//打印节点的初始平移和旋转矩阵
cerr << t.transpose() << " | " << q.coeffs().transpose() << endl;
// set first cam pose fixed
if (i == 0)
vc->setFixed(true);
// add to optimizer
//优化器添加节点
optimizer.addVertex(vc);
vertex_id++;
}
// set up point matches
for (size_t i = 0; i < true_points.size(); ++i)
{
// get two poses
//获取前述添加的节点。
/* optimizer.vertices()的返回值是一个哈希表(Map)类型,本质是std::unordered_map,
*/
VertexSE3* vp0 =
dynamic_cast(optimizer.vertices().find(0)->second);
VertexSE3* vp1 =
dynamic_cast(optimizer.vertices().find(1)->second);
// calculate the relative 3D position of the point
Vector3d pt0, pt1;
pt0 = vp0->estimate().inverse() * true_points[i];
pt1 = vp1->estimate().inverse() * true_points[i];
// add in noise
//添加高斯噪声
pt0 += Vector3d(g2o::Sampler::gaussRand(0., euc_noise),
g2o::Sampler::gaussRand(0., euc_noise),
g2o::Sampler::gaussRand(0., euc_noise));
pt1 += Vector3d(g2o::Sampler::gaussRand(0., euc_noise),
g2o::Sampler::gaussRand(0., euc_noise),
g2o::Sampler::gaussRand(0., euc_noise));
// form edge, with normals in varioius positions
Vector3d nm0, nm1;
nm0 << 0, i, 1;
nm1 << 0, i, 1;
nm0.normalize();
nm1.normalize();
//g20的二元边
Edge_V_V_GICP * e // new edge with correct cohort for caching
= new Edge_V_V_GICP();
e->setVertex(0, vp0); // first viewpoint
e->setVertex(1, vp1); // second viewpoint
EdgeGICP meas;
meas.pos0 = pt0;
meas.pos1 = pt1;
meas.normal0 = nm0;
meas.normal1 = nm1;
//定义观测值
e->setMeasurement(meas);
// e->inverseMeasurement().pos() = -kp;
meas = e->measurement();
// use this for point-plane
//约束信息(协方差矩阵的逆) = 点面的精度矩阵信息
e->information() = meas.prec0(0.01);
optimizer.addEdge(e);
}
// move second cam off of its true position
//变换第二个点云。
VertexSE3* vc =
dynamic_cast(optimizer.vertices().find(1)->second);
Eigen::Isometry3d cam = vc->estimate();
cam.translation() = Vector3d(0, 0, 0.2);
vc->setEstimate(cam);
//初始化整个图结构
optimizer.initializeOptimization();
//计算所有边的误差向量
optimizer.computeActiveErrors();
//输出优化前的误差平方
cout << "Initial chi2(before opt) = " << FIXED(optimizer.chi2()) << endl;
optimizer.setVerbose(true);
optimizer.optimize(5);
//输出优化前的误差平方
cout << "Initial chi2(after opt) = " << FIXED(optimizer.chi2()) << endl;
//打印变化矩阵
cout << endl << "Second vertex should be near 0,0,1" << endl;
cout << dynamic_cast(optimizer.vertices().find(0)->second)
->estimate().translation().transpose() << endl;
cout << dynamic_cast(optimizer.vertices().find(1)->second)
->estimate().translation().transpose() << endl;
} 测试
执行g2o自带的上述例子,最终能够打印出变换矩阵。然后将该例子单独摘出来,换入自己的数据(对应点对),也能输出变换矩阵,然后将变换矩阵作用于点云 ,结果如图3:

| 图 3 g2o--gicp |
可能早有大神预料到会是如上结果!!不得不说,g2o的优化结果也太差强人意......
真是这样吗? ......
小结
如果按照上述流程,依照g2o的官方例子,结果真是那样!!!但是和pcl的icp对比,结果是真的差,问题出在哪里?
问题出在上文中红字部分,这里依然用红字提醒自己---g2o的gicp并不能算完全的ICP求解方案。
通过分析官方代码例子可以发现,其在求解前,本质上已经默认了输入点对是对应的,在此基础上进行迭代计算,本质是依据同一组对应点对,迭代计算该组对应点之间的最优变换矩阵,对于整体两片点云来说,这样其实只是完成了一次icp计算,结果当然不理想。
换句话说,该Demo遗漏(或者g2o本就如此设计,或是自己了解不够)ICP迭代方案中对应点对的计算过程,也就是缺少了步骤1,g2o--gicp只是单纯的计算了步骤2,只得到了单次的最优变换矩阵。对于整体两片点云的icp求解问题,在进行第2次求解时,对应点对的对应关系已经发生了变化,因此g2o---gicp_demo得到的矩阵只是单次的最优矩阵,所以结果也就如图3所示。
那么如何得到整体最优结果呢? 当然是将上述步骤放入大循环中,每计算完一次g2o--gicp,变换点云,重新求解对应关系,依次迭代计算。结果图省略...
构建优化图
在充分理解了g2o自带icp例子后,回到最初自己要求解的问题。有N片粗配后的散乱点云,想要对全局点云进行全局优化配准。
所谓粗配后的全局点云,具有以下特点:
- 相邻两片点云之间具有较高重叠率;
- 相隔(至少一块点云)点云之间有或没有重叠;
- 每块点云可以有一个、零个(这个条件可以存在,构造g2o图时与条件1并不冲突)或者多个高重叠率的点云;
- 点云之间的重叠关系是对应的(即:A与B 、C、D重叠,那么BCD的重叠点云中一定也有A)。
优化目标
上述谈到的优化目标只是我们感性上的认识,但是还必须要将优化目标转化为数学表达。口述如下:优化目标 = 求解--N片三维散乱点云,以点云A为目标点云,计算所有三维散乱点云配准到A的变换矩阵,该变换矩阵使得所有对应点对的欧式距离取得最小,或者达到指定的迭代变换次数。
上述优化目标隐含:若A与C没有重叠,则C无法直接向A进行配准对齐,但是A与B,B与C有重叠,则C变换到A则需要先变换到B,由B的矩阵再变化到A,而且要保证A与B,B与C均为最优变换,换句话来说,就是B最优变换到A,C最优变换到B,则完成了A B C之间最优变换。
确认优化目标的数学表达后,还需要确认点云间的重叠率表达,口述如下:重叠率 = 两两点云对应点对的数量与该两片点云平均点数的比值。
完成上述两个数学定义后,程序的总体流程应该如下:
- 计算全局点云相互之间的对应点对与重叠率;
- 重叠点云筛选(重叠率较低的点云认为无重叠,不参与g2o图中边的构建);
g2o全局构图:
- 图节点
- 边(重点)
- 优化器与优化算法
- 基于步骤3的输出矩阵,更新全部点云的坐标;
- 重复步骤1-4,直到满足终止条件。
最终输出为优化后的全局点云及对应的变换矩阵。
程序实现
工程中使用了PCL点云库和g2o(废话),其中pcl主要用于计算点云重叠率。
通过上述【g2o--gicp_demo】可知,g2o中已经为ICP方案提供了定义好的图节点类VertexSE3和图二元边类Edge_V_V_GICP 以及边类EdgeGICP,这里直接拿来使用,省去了自定义图边、图节点麻烦(当然,若深入学习g2o,还是建议多做更多探索)。
点云数据结构
通过前述分析,可知,某点云结构应该包含如下必要内容:
- 点集;
- 是否固定;
- 变换矩阵;
- 邻接信息;
- 必要方法(最近邻点云、对应点对计算)。
构造如下:
typedef pcl::PointCloud pointcloud;
class MyPnts
{
public:
MyPnts() ;
~MyPnts();
int id;
int v_number;
vector pts;
bool fixed = false;
Isometry3d pose; //该点云的初始位姿,也是优化目标
//该点云的所有邻接信息
vector neighbours;
//当前点云在所有点云序列中的k个最近邻点云(重叠率最高的前K个)
void computeKNNearPnts(vector< std::shared_ptr>& frames, int k);
//对应点对计算
void computeClosestPointsToNeighbours(vector< shared_ptr>& frames, float thresh);
/*
* Method: calCorrespond 计算两片点云的相互对应点对的索引
* Access: public
* Returns: std::unordered_map> first 0->src,1 -> tar;
* Parameter: pointcloud::Ptr src
* Parameter: pointcloud::Ptr tar
*/
std::unordered_map> calCorrespond(MyPnts src, MyPnts tar,double dst = 10.0);
private:
}; 其中,计算当前点云与全局其他点云(除当前点云外)重叠关系、对应点对均在computeKNNearPnts()函数中实现。
造图
这是最重要也是及其容易出错的地方。
前述 [粗配后全局点云的特点],决定了g2o中图结构的特点,图边应该满足 [粗配后全局点云的特点] 的描述,伪图如下:
 全局icp 伪图 |
如上图所示,假设:全局有5片点云,则g2o图有5个节点,n1为固定节点,n1和n2有重叠,n2和n5有重叠,n1和n5也有重叠,但n1和n3 、n1 和 n4、 n2和n4等几个节点之间不存在重叠关系。
注意:这里的重叠关系,在g2o看来是约束关系,进一步的,是两片点云之间的边的链接关系,此边可能有成百上千个对应点对构成。上图中的带箭头的边仅表示示意,并非真正的图边。
在清楚了图结构后,构造图代码如下:
void G2oPCL::global_icp2(std::vector> &pnts)
{
using namespace g2o;
using namespace std;
using namespace Eigen;
g2o::SparseOptimizer optimizer;
optimizer.setVerbose(false);
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(
g2o::make_unique(g2o::make_unique>()));
optimizer.setAlgorithm(solver);
//节点
for (int i = 0; i < pnts.size(); ++i) {
g2o::VertexSE3 *vc = new VertexSE3();
vc->setEstimate( (*pnts[i]).pose);
vc->setId(i); // vertex id
if (i == 0) {
vc->setFixed(true);
(*pnts[i]).fixed = true;
}
optimizer.addVertex(vc);
}
//构造全局边关系
for (int i = 0; i < pnts.size(); ++i) {
std::shared_ptr ¤t = pnts[i];
int current_nebor = current->neighbours.size();
for (int j = 0; j < current_nebor; ++j) {
OutgoingEdge *oe = current->neighbours[j];
int nearIdx = oe->neighbourIdx;
std::shared_ptr &dst = pnts[nearIdx];
g2o::VertexSE3* vp0 =
dynamic_cast(optimizer.vertices().find(nearIdx)->second); //dstCloud
g2o::VertexSE3* vp1 =
dynamic_cast(optimizer.vertices().find(current->id)->second); //srcCloud
for (auto cor : oe->correspondances) {
g2o::Edge_V_V_GICP * e = new g2o::Edge_V_V_GICP();
e->setVertex(0, vp0);
e->setVertex(1, vp1);
g2o::EdgeGICP meas;
meas.pos0 = dst->pts[cor.second];
meas.pos1 = current->pts[cor.first];
e->setMeasurement(meas);
//use this for point-point
e->information().setIdentity();
optimizer.addEdge(e);
}
}
}
optimizer.initializeOptimization();
optimizer.computeActiveErrors();
double chiInit = optimizer.chi2(); //stop innerround if we get 100% better
optimizer.optimize(100);
cout << "round: " << "s" << " chi2: " << FIXED(chiInit) << endl;
for (int i = 0; i < pnts.size(); ++i) {
VertexSE3 *res = dynamic_cast(optimizer.vertices().find(i)->second);
Isometry3d transAndRot = res->estimate();
MyPnts &mypnts = *pnts[i];
for (int j = 0; j < mypnts.v_number; ++j) {
mypnts.pts[j] = transAndRot * mypnts.pts[j];
}
}
} 在上述代码中,不仅构造了图结构,设置了各个节点之间的相互关系,而且还更新了点的坐标,为方便下次迭代中计算对应点对提供了方便。
至此,基于g2o解决开始提到的问题框架基本完成,最终主程序代码如下:
int main()
{
std::unique_ptr gp = std::make_unique();
clock_t begin, end;
begin = clock();
std::vector> pnts;
loadPnts(pnts, "");
//计算与目标点云重叠率最高的两片点云
computeNumbers(pnts, 2);
int N = 40;
for (int i = 0; i global_icp2(pnts);
}
end = clock();
double t = (end - begin) / 1000.0;
std::cout << "\n\n 执行时间是:" << t << std::endl;
std::cout << "保存结果到本地" << std::endl;
savePnts(pnts);
} 实验测试
完成上述准备与代码编程后,将自己的数据(图1和图2所示点云),输入优化系统中。
测试一
在此次测试中,computeNumbers(pnts, 2)第二个参数为2,也就是构建了一个二元超图(所谓二元超图,只单纯是自己的定义,完全不与其他任何g2o程序或代码或教程相符合,也不具备真实数学意义,同样不适用于其他g2o学习过程,在这里所谓二元超图,只单纯表示图中每个节点有两个关系节点,同样,每个节点只有两个约束关系),最终结果如下:
 图4 点云底面 |
 图5 局部细节 |
将图4 图5分别与图1 图2进行对比,肉眼可见效果提升了很多。
执行过程中截图如下:
 图 6 图 6 |
 图 7 图 7 |
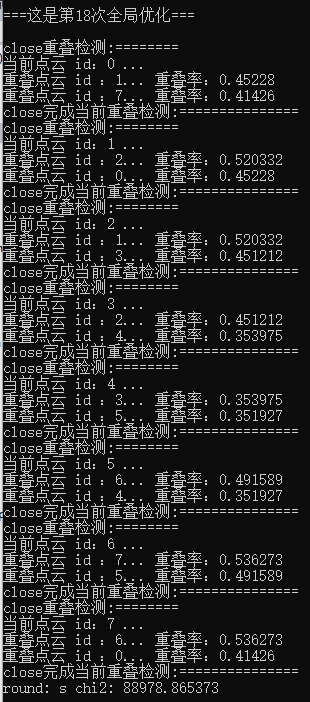 图 8 图 8 |
 图 9 图 9 |
观察图6--图9,因为在computeNumbers(pnts, 2);传入的参数为2,所以这里只计算了每块点云重叠率最高的两块,打印信息可是看出,id为0的点云重叠率最高的是id为1和id为2的,id为3的点云重叠率最高的是id为2和id为4的,也就是说,当前带点云重叠率最高的是其两片相邻的点云,这是符合自己的实际情况的;继续看,随着迭代过程次数的增加,每块点云之间的重叠率是不断变化的,这也同样符合实际情况;最后,看误差参数估计ch2的输出变化 62w-->24w-->8w-->5w(全局大概20w左右的对应点对),逐步减小,也就是说对应点对之间的全局欧式距离平方和在逐步减小,同样符合实际情况。
该二元超图结构如下:
 图10 二元图 图10 二元图 |
测试二
设置computeNumbers(pnts, N);参数N为3时,构建一张三元超图。
在三元超图下,最终效果和图4 图5类似,同样认为完成了全局优化;期间,程序执行过程中信息输出如下:
 |
 |
根据上述打印信息可知,构造的三元图结构如下所示:
 |
至此,基本完成了自己最初的目的,欣喜....
总结&题外话
自己目前也只是g2o新手村普通村民,且上述描述也并非真正意义上的slam问题,所述描述中只是自己针对所面临问题探求思路,不具备教学性、更不具权威性(有些夸大),仅作个人记录与兴趣交流。
上述描述的求解方案和思路,应该可以用来求解散乱点云多视角全局配准优化问题,而且也应该算是一个通用(不仅仅限于相邻点云重叠)的求解方案。
G2O在slam后端中使用的比较多,官方提供的demo大多也是slam2d、slam3d等,但又不仅限于此。因为针对自己所面临的问题,并没有将其向slam方向深入扩展,所以也并没有从其他教程所述那样,从slam2d例程入手,而是选择了自己较为熟悉的ICP领域。
不过话又说回来,自己所面的问题从整体解决思路上看,又可以作为是一个典型的slam优化问题:已知多个视角闭环的三维点云,通过求取路标点,求解全局相机位姿。
总之,我知道:g2o可以用来解决非线性优化问题。
啰里啰唆......
(顺便吐槽图片排版是真烂)