python 服从正态分布下概率密度函数
python 服从正态分布下概率密度函数
服从正太分布下,概率密度函数公式
x: 是随机抽样的数值,取值范围从负无穷大到正正无穷大 对服从正太分布下,概率密度函数的理解: (2) 概率密度函数的图像(曲线图像)关于x=μ对称 (3) 标准差σ越大, 则图像峰值(峰值也就是概率最大值,即:峰值=f(x=μ))越小 (4) 概率最小值趋近于0 应用python绘制图像 显示图像 稍微修改均值和标准差后,重新绘图, 如下: 图像显示: 再次修改代码对标准差和均值重新赋值(可跳过不用看代码, 直接看图像) 图像显示: 最后: 本人又另写一篇关于服从正太分布概率 离散情况下 概率密度函数和累积密度函数的文章. 有疑惑的可以查看一下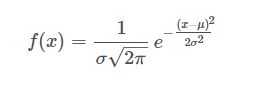
公式解释:
f(x): 是某样本(样本以数值形式表现)为某数值时发生的概率
0
e: 是自然数
σ: 是样本的标准差
μ:是样本的算术平均值(也叫均值)
(1) 当自变量x=μ时,f(x)取的最大值, 最大值=f(x=μ)
即:当自变量取值为均值时,发生的概率最大(或者说:发生概率最大的数是均值)"""
绘制正太分布函数曲线图
"""
import matplotlib.pyplot as plt
import math
import numpy as np
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False#解决保存图像时负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
x = np.linspace(-10,30,num=1000) # x轴的取值范围
std1 = 1 # 定义标准差, 并输入标准差
mean1 = 10 # 定义均值,并输入均值
fx1 = 1 / (std1 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean1) ** 2) / (2 * std1 ** 2)) # 概率密度函数公式
std2 = 2
mean2 = 10
fx2 = 1 / (std2 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean2) ** 2) / (2 * std2 ** 2)) # 概率密度函数公式
std3 = 4
mean3= 10
fx3 = 1 / (std3 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean3) ** 2) / (2 * std3 ** 2)) # 概率密度函数公式
std4 = 8
mean4 = 10
fx4 = 1 / (std4 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean4) ** 2) / (2 * std4 ** 2)) # 概率密度函数公式
# 多条曲线在同一张图上进行对比
plt.plot(x, fx1,label = 'std1 = 1') # 绘制概率密度函数图像
plt.plot(x,fx2,label = 'std2 = 2')
plt.plot(x,fx3,label = 'std3 = 4')
plt.plot(x,fx4,label = 'std4 = 8')
plt.legend() # 显示标签 label
plt.xlabel("数值")
plt.ylabel('数值的概率')
plt.title('服从正太分布的概率密度图')
plt.show() # 显示图像

由图像可知道: 标准差std 越大, 则峰值越小.(代码设置了均值相同)import matplotlib.pyplot as plt
import math
import numpy as np
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False#解决保存图像时负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
x = np.linspace(-10,30,num=1000) # x轴的取值范围
std1 = 3 # 定义标准差, 并输入标准差
mean1 = 6 # 定义均值,并输入均值
fx1 = 1 / (std1 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean1) ** 2) / (2 * std1 ** 2)) # 概率密度函数公式
std2 = 3
mean2 = 10
fx2 = 1 / (std2 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean2) ** 2) / (2 * std2 ** 2)) # 概率密度函数公式
std3 = 3
mean3= 12
fx3 = 1 / (std3 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean3) ** 2) / (2 * std3 ** 2)) # 概率密度函数公式
std4 = 3
mean4 = 18
fx4 = 1 / (std4 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean4) ** 2) / (2 * std4 ** 2)) # 概率密度函数公式
# 多条曲线在同一张图上进行对比
plt.plot(x, fx1,label = '均值 = 6') # 绘制概率密度函数图像
plt.plot(x,fx2,label = '均值 = 10')
plt.plot(x,fx3,label = '均值 = 12')
plt.plot(x,fx4,label = '均值 = 18')
plt.legend() # 显示标签 label
plt.xlabel("数值")
plt.ylabel('数值的概率')
plt.title('服从正太分布的概率密度图')
plt.show() # 显示图像

由图像看出, 当标准差相同时(代码设置标准差相同), 峰值相同, 均值不同时, 对称轴位置不同import matplotlib.pyplot as plt
import math
import numpy as np
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False#解决保存图像时负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
x = np.linspace(-10,30,num=1000) # x轴的取值范围
std1 = 3 # 定义标准差, 并输入标准差
mean1 = 6 # 定义均值,并输入均值
fx1 = 1 / (std1 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean1) ** 2) / (2 * std1 ** 2)) # 概率密度函数公式
std2 = 5
mean2 = 10
fx2 = 1 / (std2 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean2) ** 2) / (2 * std2 ** 2)) # 概率密度函数公式
std3 = 6
mean3= 12
fx3 = 1 / (std3 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean3) ** 2) / (2 * std3 ** 2)) # 概率密度函数公式
std4 = 2
mean4 = 18
fx4 = 1 / (std4 * pow(2 * math.pi, 0.5)) * np.exp(-((x - mean4) ** 2) / (2 * std4 ** 2)) # 概率密度函数公式
# 多条曲线在同一张图上进行对比
plt.plot(x, fx1,label = '均值 = 6, 标准差=3') # 绘制概率密度函数图像
plt.plot(x,fx2,label = '均值 = 10, 标准差=5')
plt.plot(x,fx3,label = '均值 = 12, 标准差=6')
plt.plot(x,fx4,label = '均值 = 18, 标准差=2')
plt.legend() # 显示标签 label
plt.xlabel("数值")
plt.ylabel('数值的概率')
plt.title('服从正太分布的概率密度图')
plt.show() # 显示图像

通过图像可以观查出均值和标准差对概率的影响, 验证了上述的结论